Number-Systems
Question 1 |
bias of 127.
S : 1 E : 10000001 F : 11110000000000000000000
Here S, E and F denote the sign, exponent and fraction components of the floating point representation.
The decimal value corresponding to the above representation (rounded to 2 decimal places) is _______
-7.75 |
Sign bit S= 1. The given number is a negative number.
Biased Exponent E = 27 + 1= 129
Actual Exponent e = E-127
= 129- 127
= 2
The decimal value= (-1)s x 1.M x 2e
= (-1) 1 x 1.1111 x 22
= - (111.11)
= - (7 + 0.75)
= -7.7
Question 2 |
21 | |
528
| |
D2 | |
15 |
On converting (210)3 in decimal, we will get:=>
2*32+1*3=2*9+3=2110
=>(15)16
Question 3 |
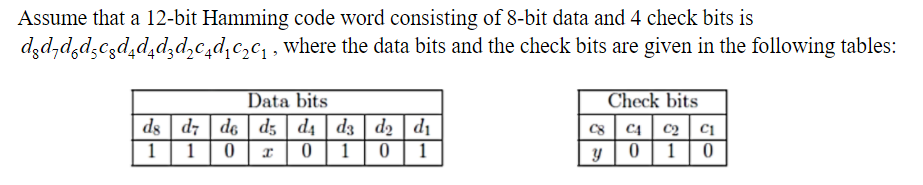
Which one of the following choices gives the correct values of x and y?
x is 1 and y is 1 | |
x is 0 and y is 1 | |
x is 1 and y is 0 | |
x is 0 and y is 0 |
C2 checks the bits d1, d3, d4, d6, d7.
C2=1, d1= 1, d3= 1, d4= 0, d6= 0, d7= 1.
The number of 1s is even. So, even parity is used in this problem.
C1 checks the bits d1, d2, d4, d5, d7.
C1=0, d1= 1, d2= 0, d4= 0, d5= x, d7= 1.
As the parity used is even parity, the value of d5 should be 0.
x=d5=0
C8 checks the bitsa d5, d6, d7, d8.
C8=y, d5= x=0, d6= 0, d7= 1, d8= 1.
As the parity used is even parity, the value of C8 should be 0.
C8=y=0.
x=y=0.
Question 4 |
Convert the following numbers in the given bases into their equivalents in the desired bases.
(a) 110.101)2 = x)10
(b) 1118)10 = y)H
(a) 6.625, (b) (45E)H |
= 4 + 2 + 0 + 0.5 + 0 + 0.125
= 6.625
(b) 1118 mod 16 = E, quotient = 69
69 mod 16 = 5, quotient = 4
4 mod 16 = 4
Writing the mods result in reverse order gives (45E)H.
Question 5 |
Consider n-bit (including sign bit) 2’s complement representation of integer number. The range of integer values, N, that can be represented is _________ ≤ N ≤ _________
-2n-1 to 2n-1 - 1 |
Question 6 |
Write a program in 8085 Assembly language to Add two 16-bit unsigned BCD(8-4-2-1 Binary Coded Decimal) number. Assume the two input operands are in BC and DE Register pairs. The result should be placed in the register pair BC. (Higher order register in the register pair contains higher order digits of operand)
Theory Explanation. |
Question 7 |
The number of 1’s in the binary representation of
(3*4096 + 15*256 + 5*16 + 3) are:
8 | |
8 | |
10 | |
12 |
= (11000000000000)2
15 × 256 = 15 × 28
= (111100000000)2
5 × 16 = 5 × 24
= (1010000)2
3 = (11)2
Hence, all binary numbers,

∴ 101's
Question 8 |
(a) An asynchronous serial communication controller that uses a start stop scheme for controlling the serial I/O of a system is programmed for a string of length seven bits, one parity bit (odd parity) and one step bit. The
transmission rate is 1200 bits/second.
(i) What is the complete bit stream that is transmitted for the string ‘0110101’?
(ii) How many such strings can be transmitted per second?
(b) Consider a CRT display that has a text mode display format of 80 × 25 characters with a 9 × 12 character cell. What is the size of the video buffer RAM for the display to be used in monochrome (1 bit per pixel) graphics mode?
Theory Explanation. |
Question 9 |
Consider three registers R1, R2 and R3 that store numbers in IEEE-754 single precision floating point format. Assume that R1 and R2 contain the values (in hexadecimal notation) 0x42200000 and 0xC1200000, respectively.
If R3 = R1/R2, what is the value stored in R3?
0x40800000 | |
0x83400000 | |
0xC8500000 | |
0xC0800000 |

R1 = 1.0100..0 X 2132-127
= 1.0100..0 X 25
= 101.0 X 23
= 5 X 8
= 40

R2 = (-1) x 1.0100..0 X 2130-127
= (-1) x 1.0100..0 X 23
= (-1) x 101.0 X 21
= (-1) x5 X 2
= -10
R3 = R1/R2
= -4
= (-1)x 1.0 x 22
Sign = 1
Mantissa = 000..0
Exponent = 2+127 = 129

R3 = 1100 0000 1000 000..0
= 0x C 0 8 0 0 0 0 0
Question 10 |
Consider the following floating point number representation

The exponent is in 2's complement representation and mantissa is in the sign magnitude representation. The range of the magnitude of the normalized numbers in this representation is
0 to 1 | |
0.5 to 1 | |
2-23 to 0.5 | |
0.5 to (1-2-23) |
Question 11 |
In 16-bit 2's complement representation, the decimal number -28 is:
1111 1111 1110 0100 | |
1111 1111 0001 1100 | |
0000 0000 1110 0100 | |
1000 0000 1110 0100 |
1’s complement = 1111 1111 1110 0011
2’s complement = 1’s complement + 1
2’s complement = 1111 1111 1110 0100 = (-28)
Question 12 |
Two numbers are chosen independently and uniformly at random from the set {1, 2, ..., 13}. The probability (rounded off to 3 decimal places) that their 4-bit (unsigned) binary representations have the same most significant bit is ______.
0.502 | |
0.461 | |
0.402 | |
0.561 |
1 - 0001
2 - 0010
3 - 0011
4 - 0100
5 - 0101
6 - 0110
7 - 0111
8 - 1000
9 - 1001
10 - 1010
11 - 1011
12 - 1100
13 - 1101
The probability that their 4-bit binary representations have the same most significant bit is
= P(MSB is 0) + P(MSB is 1)
= (7×7)/(13×13) + (6×6)/(13×13)
= (49+36)/169
= 85/169
= 0.502
Question 13 |
Consider Z = X - Y, where X, Y and Z are all in sign-magnitude form. X and Y are each represented in n bits. To avoid overflow, the representation of Z would require a minimum of:
n bits | |
n + 2 bits | |
n - 1 bits | |
n + 1 bits |
To store overflow/carry bit there should be extra space to accommodate it.
Hence, Z should be n+1 bits.
Question 14 |
Given √224)r = 13)r.
The value of the radix r is:
10 | |
8 | |
5 | |
6 |
Convert r base to decimal.
√2r2 + 25 + 4 = r + 3
Take square both sides,
2r2 + 2r + 4 = r2 + 6r + 9
r2 - 4r - 5 = 0
r2 - 5r + r - 5 = 0
r(r - 5) + (r - 5) = 0
r = -1, 5
r cannot be -1,
So r = 5 is correct answer.
Question 15 |
The octal representation of an integer is (342)8. If this were to be treated as an eight-bit integer is an 8085 based computer, its decimal equivalent is
226 | |
-98 | |
76 | |
-30 |
If this can be treated as 8 bit integer, then the first becomes sign bit i.e., '1' then the number is negative.
8085 uses 2's complement then
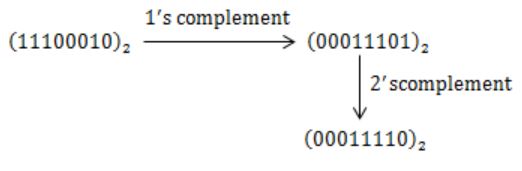
⇒ -30
Question 16 |
Suppose the domain set of an attribute consists of signed four digit numbers. What is the percentage of reduction in storage space of this attribute if it is stored as an integer rather than in character form?
80% | |
20% | |
60% | |
40% |
We have four digits. So to represent signed 4 digit numbers we need 5 bytes, 4 bytes for four digits and 1 for the sign.
So required memory = 5 bytes.
Now, if we use integer, the largest no. needed to represent is 9999 and this requires 2 bytes of memory for signed representation.
9999 in binary requires 14 bits. So, 2 bits remaining and 1 we can use for sign bit.
So, memory savings,
= 5 - 2/5 × 100
= 60%
Question 17 |
Booth’s coding in 8 bits for the decimal number –57 is
0 – 100 + 1000 | |
0 – 100 + 100 - 1 | |
0 – 1 + 100 – 10 + 1 | |
00 – 10 + 100 - 1 |

Question 18 |
Zero has two representations in
Sign magnitude | |
1’s complement | |
2’s complement | |
None of the above | |
Both A and B |
+0 = 0000
-0 = 1000
1's complement:
+0 = 0000
-0 = 1111
Question 19 |
The number 43 in 2’s complement representation is
01010101 | |
11010101 | |
00101011 | |
10101011 |
Question 20 |
Consider the values A = 2.0 x 1030, B = -2.0 x 1030, C = 1.0, and the sequence
X: = A + B Y: = A + C
X: = X + C Y: = Y + B
executed on a computer where floating-point numbers are represented with 32 bits. The values for X and Y will be
X = 1.0, Y = 1.0 | |
X = 1.0, Y = 0.0 | |
X = 0.0, Y = 1.0 | |
X = 0.0, Y = 0.0 |
A = 2.0 * 1030, C = 1.0
So, A + C should make the 31st digit to 1, which is surely outside the precision level of A (it is 31st digit and not 31st bit). So, this addition will just return the value of A which will be assigned to Y.
So, Y + B will return 0.0 while X + C will return 1.0.
Question 21 |
The 2’s complement representation of (-539)10 in hexadecimal is
ABE | |
DBC | |
DE5 | |
9E7 |
For (-539)10 = (1101 1110 0100)2
1's complement = (1101 1110 0100)2
2's complement = (1101 1110 0101)2
= (DE5)16
Question 22 |
Consider the circuit shown below. The output of a 2:1 Mux is given by the function (ac' + bc).
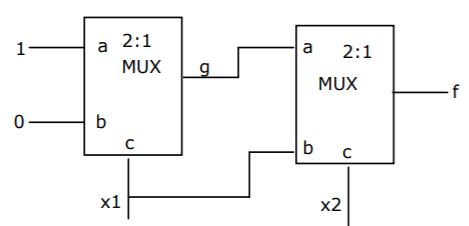
Which of the following is true?
f = x1' + x2 | |
f = x1'x2 + x1x2' | |
f = x1x2 + x1'x2' | |
f = x1 + x2' |
g = (1 and x1’) or (0 and x1)
g = x1’
f = ac’ + bc
f = (a and x2′) or (b and x2)
f = (g and x2′) or (x1 and x2)
f = x1’x2’ + x1x2
Question 23 |
The decimal value 0.25
is equivalent to the binary value 0.1 | |
is equivalent to the binary value 0.01 | |
is equivalent to the binary value 0.00111… | |
cannot be represented precisely in binary |
Multiply 0.25 by 2.
0.25×2 = 0.50 (product)
Fractional part = 0.50
Carry = 0
2nd Multiplication iteration:
Multiply 0.50 by 2.
0.50×2 = 1.00 (product)
Fractional part = 0.00
Carry = 1
The fractional part in the 2nd iteration becomes zero and so we stop the multiplication iteration.
Carry from 1st multiplication iteration becomes MSB and carry from 2nd iteration becomes LSB. So the result is 0.01.
Question 24 |
The 2’s complement representation of the decimal value -15 is
1111 | |
11111 | |
111111 | |
10001 |
-15 = 11111
1's complement = 10000
2's complement = 10001
Question 25 |
Sign extension is a step in
floating point multiplication | |
signed 16 bit integer addition | |
arithmetic left shift | |
converting a signed integer from one size to another |
Question 26 |
In 2’s complement addition, overflow
is flagged whenever there is carry from sign bit addition | |
cannot occur when a positive value is added to a negative value | |
is flagged when the carries from sign bit and previous bit match | |
None of the above |
Question 27 |
Consider the following 32-bit floating-point representation scheme as shown in the formal below. A value is specified by 3 fields, a one bit sign field (with 0 for positive and 1 for negative values), a 24 bit fraction field (with the binary point being at the left end of the fraction bits), and a 7 bit exponent field (in excess-64 signed integer representation, with 16 being the base of exponentiation). The sign bit is the most significant bit.
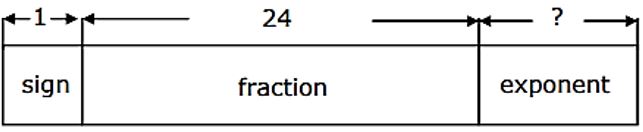
(a) It is required to represent the decimal value –7.5 as a normalized floating point number in the given format. Derive the values of the various fields. Express your final answer in the hexadecimal.
(b) What is the largest values that can be represented using this format? Express your answer as the nearest power of 10.
Theory of Explanation is given below. |
Question 28 |
b7 b6 b5 b4 b3 b2 b1 b0
where the position of the binary point is between b3 and b2 . Assume b7 is the most significant bit.
Some of the decimal numbers listed below cannot be represented exactly in the above representation:
(i) 31.500
(ii) 0.875
(iii) 12.100
(iv) 3.001
Which one of the following statements is true?
None of (i), (ii), (iii), (iv) can be exactly represented
| |
Only (ii) cannot be exactly represented | |
Only (iii) and (iv) cannot be exactly represented | |
Only (i) and (ii) cannot be exactly represented |
= 16 + 8 + 4 + 2 + 1 + 0.5
= (31.5)10
(ii) (0.875)10 = (00000.111)2
= 2-1 + 2-2 + 2-3
= 0.5 + 0.25 + 0.125
= (0.875)10
(iii) (12.100)10
It is not possible to represent (12.100)10
(iv) (3.001)10 It is not possible to represent (3.001)10
Question 29 |
Consider the number given by the decimal expression:
163 * 9 + 162 * 7 + 16 * 5 + 3
The number of 1’s in the unsigned binary representation of the number is ________.
9 |
(9753)16
It's binary representation is,
1001011101010011
∴ The no. of 1's is 9.
Question 30 |
When two 4-bit binary number A = a3a2a1a0 and B = b3b2b1b0 are multiplied, the digit c1 of the product C is given by _________
c1 = b1a0 ⊕ a1b0 |

⇒ c1 = b1a0 ⊕ a1b0
Question 31 |
exponent = 00000001 and mantissa = 00000000000000000000001 | |
exponent = 00000001 and mantissa = 00000000000000000000000 | |
exponent = 00000000 and mantissa = 00000000000000000000000 | |
exponent = 00000000 and mantissa = 00000000000000000000001 |
The smallest biased exponent for the normalized number is E= 1.
The smallest Mantissa M = 000...0
The smallest positive normalized number = 1.M x 2 E-127
= 1.0 x 2 -126 .
= 2 -126
Question 32 |
0x4243 | |
0x6665 | |
0x0001 | |
0x0100 |
It is given that the unsigned integer is 2-bytes long. It needs 4 hexadecimal digits.
We know the big-endian and little-endian computers differ in how the data is stored in memory.
In little endian machines, the last byte of binary representation of the multibyte data-type is stored first. On the other hand, in big endian machines, the first byte of binary representation of the multibyte data-type is stored first.
In the hexadecimal representation of the 2-byte number on the little endian machine, the first two hexadecimal digits are for one byte and the last two hexadecimal digits are for the second byte. On the big endian machine it is the other way round.
It is given that the value in little endian representation is 255 more than the value in the big endian machine.
From the given options
A). In little endian = 0x4243 in binary (0100 0010 0100 0011) which has decimal value = 16963
On big endian = 0x4342 in binary (0100 0011 0100 0010) which has decimal value = 17218
Here the big endian value is higher than the little endian value. So this is not the correct option.
B). In little endian 0x6665 in binary (0110 0110 0110 0101) which has the decimal value = 26213
In big endian 0x6566 in binary (0110 0101 0110 0110) which has the decimal value = 25958
The difference = 26213 - 25958 = 255. So this is also the correct option.
C). In little endian 0x0001 in binary (0000 0000 0000 0001) which has the decimal value = 1.
In big endian 0x0100 in binary (0000 0001 0000 0000) has decimal value = 256.
But here also the big endian value is higher than the little endian. So this is not the correct option.
D). On the little endian machine for hexadecimal number 0x0100 in binary (0000 0001 0000 0000) which has decimal value = 256. On a big endian machine it is 0x 0001 in binary (0000 0000 0000 0001) which has decimal value = 1
The difference in value of little endian to big endian is 256-1 = 255.
Hence 2, 4 are the correct options.
Question 33 |
3 |
x=1 and y=2
x+y= 1+2=3
Question 34 |
R1 = 1011 and R2 = 1110 | |
R1 = 1100 and R2 = 1010 | |
R1 = 0011 and R2 = 0100 | |
R1 = 1001 and R2 = 1111 |

Question 35 |

Which one of the following is FALSE?
A + C = 0 | |
C = A + B | |
B = 3 C | |
( B - C ) > 0 |

A= -12, B= +36 and C= +12
A+C= 0
B=3C
(B-C)>0
C≠A+B
Question 36 |
The number (123456)8 is equivalent to
(A72E)16 and (22130232)4 | |
(A72E)16 and (22131122)4 | |
(A73E)16 and (22130232)4 | |
(A62E)16 and (22120232)4
|
= (00 1010 0111 0010 1110)2
= (A72E)16
Also,
(001 010 011 100 101 110)2
= (00 10 10 01 11 00 10 11 10)2
= (22130232)4
Question 37 |
Consider a parity check code with three data bits and four parity check bits. Three of the code words are 0101011, 1001101 and 1110001. Which of the following are also code words?
1. 0010111 2. 0110110 3. 1011010 4. 0111010
1 and 3 | |
1, 2 and 3 | |
2 and 4 | |
1, 2, 3 and 4 |
Given transmitted codewords are
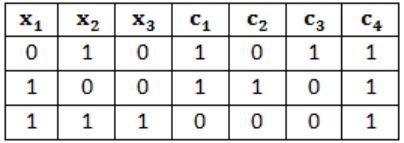
By inspection we can find the rule for generating each of the parity bits,
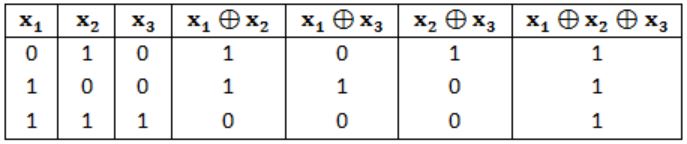
Now from above we can see that (I) and (III) are only codewords.
Question 38 |
(34.4)8 × (23.4)8 evaluates to
(1053.6)8 | |
(1053.2)8 | |
(1024.2)8 | |
None of these |
(34.4)8 = 3×81 + 4×80 + 4×8-1
= 24 + 4 + 0.5
= (28.5)10
(23.4)8 = 2×81 + 3×80 + 4×8-1
= 16 + 3 + 0.5
= (19.5)10
Now,
(28.5)10 × (19.5)01 = (555.75)10
Now,
(555.75)10 = ( ? )8
To convert the integer part,
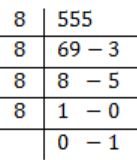
We get, 1053.
To convert the fractional part, keep multiplying by 8 till decimal part becomes 0,

∴ (555.75)10 = (1053.6)8
Question 39 |
The addition of 4-bit, two’s complement, binary numbers 1101 and 0100 results in
0001 and an overflow | |
1001 and no overflow | |
0001 and no overflow | |
1001 and an overflow |
2's complement of 1100 = 1100
Add = 1111
Now convert 1111 to normal form.
⇒ 0000 (1's complement)
⇒ 0001 (2's complement) No carry bit.
Question 40 |
When multiplicand Y is multiplied by multiplier X = xn-1xn-2 ...x0 using bit-pair recoding in Booth's algorithm, partial products are generated according to the following table.
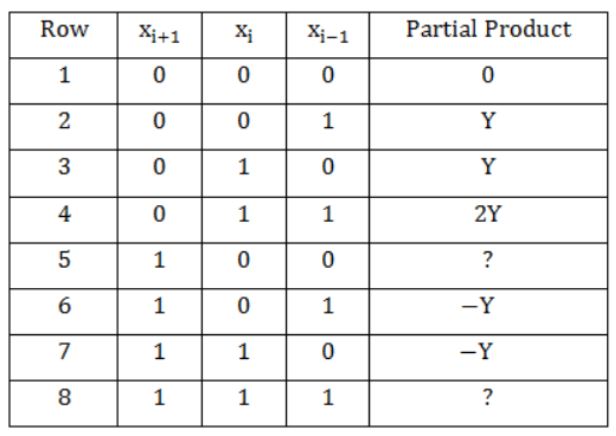
The partial products for rows 5 and 8 are
2Y and Y | |
-2Y and 2Y | |
-2Y and 0 | |
0 and Y |
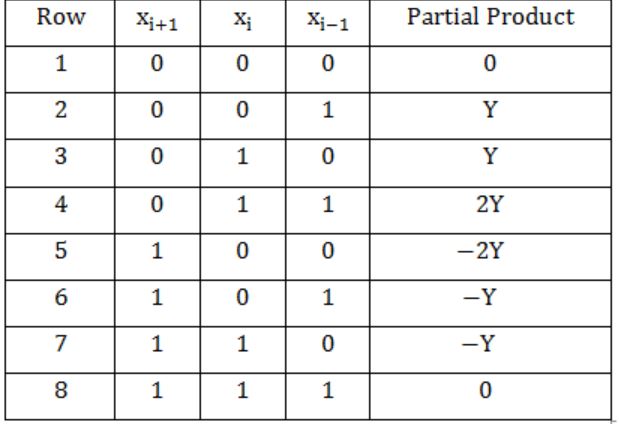
⇒ -2Y and 0
Question 41 |
(C012.25)H – (10111001110.101)B =
(135103.412)O | |
(564411.412)O | |
(564411.205)O | |
(135103.205)O |
= 1100000000010010.00100101 - 0000010111001110.10100000
= 1011101001000011.10000101
= 1011101000011.100001010
= (135103.412)O
Question 42 |
The following bit pattern represents a floating point number in IEEE 754 single precision format
110000011101000000000000000000000The value of the number in decimal form is
-10 | |
-13 | |
-26 | |
None of these |
Exponent bits - 10000011
Exponent can be added with 127 bias in IEEE single precision format then outval exponent
= 10000011 - 127
= 131 - 127
= 4
→ In IEEE format, an implied 1 is before mantissa, and hence the outval number is
→ 1.101 × 24 = -(11010)2 = -26
Question 43 |
A processor that has carry, overflow and sign flag bits as part of its program status word (PSW) performs addition of the following two 2's complement numbers 01001101 and 11101001. After the execution of this addition operation, the status of the carry, overflow and sign flags, respectively will be:
1, 1, 0 | |
1, 0, 0 | |
0, 1, 0 | |
1, 0, 1 |

Carry flag = 1
Overflow flag = 0
Sign bit = 0 (MSB bit is 0)
Overflow flag:
In computer processors, the overflow flag is usually a single bit in a system status register used to indicate when an arithmetic overflow has occurred in an operation.
Question 44 |
The two numbers given below are multiplied using the Booth's algorithm.
Multiplicand : 0101 1010 1110 1110 Multiplier: 0111 0111 1011 1101How many additions/Subtractions are required for the multiplication of the above two numbers?
6 | |
8 | |
10 | |
12 |
Now we have some values defined for pair of bits in Booth’s Algorithm,
00 → 0
11 → 0
01 → -1
10 → 1
Now after adding 0 to the LSB of the multiplier, start traversing from left to right and accordingly put the values defined above.

Hence, total 8 additions / subtractions required.
Question 45 |
The exponent of a floating-point number is represented in excess-N code so that:
The dynamic range is large. | |
The precision is high. | |
The smallest number is represented by all zeros. | |
Overflow is avoided. |
Question 46 |
Assuming all numbers are in 2's complement representation, which of the following numbers is divisible by 11111011?
11100111 | |
11100100 | |
11010111 | |
11011011 |
MSB bit is '1' then all numbers are negative
1's complement = 00000100
2's complement = 00000100 + 00000001 = 00000101 = -5
(A) 11100111 - (-25)10
(B) 11100100 - (-28)10
(C) 11010111 - (-41)10
(D) 11011011 - (-37)10
Answer: Option A (-25 is divisible by -5)
Question 47 |
The following is a scheme for floating point number representation using 16 bits.

Let s, e, and m be the numbers represented in binary in the sign, exponent, and mantissa fields respectively. Then the floating point number represented is:

What is the maximum difference between two successive real numbers representable in this system?
2-40 | |
2-9 | |
222 | |
231 |
The largest number is 1.111111111× 262-31 = (2−2−9)×231
Second largest number is 1.111111110×262-31 = (2−2-8)×231
Difference = (2−2−9)×231 - (2−2-8)×231
= (2-8−2−9) ×231
= 2−9×231
= 222
Question 48 |
If 73x (in base-x number system) is equal to 54y (in base-y number system), the possible values of x and y are
8, 16 | |
10, 12 | |
9, 13 | |
8, 11 |
7x+3 = 5y+4
7x-5y = 1
Only option (D) satisfies above equation.
Question 49 |
What is the result of evaluating the following two expressions using three-digit floating point arithmetic with rounding?
(113. + -111.) + 7.51 113. + (-111. + 7.51)
9.51 and 10.0 respectively
| |
10.0 and 9.51 respectively
| |
9.51 and 9.51 respectively | |
10.0 and 10.0 respectively |
= (2) + 7.51
= 9.51 (✔️)
113. + (-111. + 7.51)
= 113. + (-103.51)
= 113. + -103
= 10 (✔️)
Question 50 |
Let A = 1111 1010 and B = 0000 1010 be two 8-bit 2's complement numbers. Their product in 2's complement is
1100 0100
| |
1001 1100
| |
1010 0101
| |
1101 0101 |
B = 0000 1010 = 1010 [2's complement number]
A×B = -6×10 = - 6010
⇒ -6010 = 101111002
= 110000112 (1's complement)
= 110001002 (2's complement)
Question 51 |
110 |
Question 52 |
0x404C2EF4 | |
0x405C2EF4 | |
0xC15C2EF4 | |
0xC14C2EF4 |
Question 53 |
3 | |
4 | |
5 | |
6 |
Question 54 |
A+B | |
A-B | |
B-A | |
2*B |
Question 55 |
Let X be the number of distinct 16-bit integers in 2’s complement representation. Let Y be the number of distinct 16-bit integers in sign magnitude representation.
Then X-Y is _________.
1 | |
2 | |
3 | |
4 |
Since range is - 215 to 215 - 1
Y = 216 - 1
Here, +0 and -0 are represented separately.
X - Y = 216 - (216 - 1)
= 1
Question 56 |
The 16-bit 2’s complement representation of an integer is 1111 1111 1111 0101; its decimal representation is __________.
-11 | |
-12 | |
-13 | |
-14 |
It is a negative number because MSB is 1.
Magnitude of 1111 1111 1111 0101 is 2’s complement of 1111 1111 1111 0101.
1111 1111 1111 0101
0000 0000 0000 1010 : 1’s Complement
0000 0000 0000 1011 : 2’s complement
= (11)10
Hence, 1111 1111 1111 0101 = -11
Question 57 |
The representation of the value of a 16-bit unsigned integer X in hexadecimal number system is BCA9. The representation of the value of X in octal number system is
136251 | |
736251 | |
571247 | |
136252 |
Each hexadecimal digit is equal to a 4-bit binary number. So convert
X = (BCA9)16 to binary

Divide the binary data into groups 3 bits each because each octal digit is represented by 3-bit binary number.
X = (001 011 110 010 101 001)2
Note: Two zeroes added at host significant position to make number bits of a multiple of 3 (16 + 2 = 18)
X = (136251)8
Question 58 |
Given the following binary number in 32-bit (single precision) IEEE-754 format:
The decimal value closest to this floating-point number is
1.45 × 101 | |
1.45 × 10-1 | |
2.27 × 10-1 | |
2.27 × 101 |

For single-precision floating-point representation decimal value is equal to (-1)5 × 1.M × 2(E-127)
S = 0
E = (01111100)2 = (124).
So E – 127 = - 3
1.M = 1.11011010…0
= 20 + 2(-1) + 2(-1) + 2(-4) + 2(-5) + 2(-7)
= 1+0.5+0.25+0.06+0.03+0.007
≈ 1.847
(-1)5 × 1.M × 2(E-127)
= -10 × 1.847 × 2-3
≈ 0.231
≈ 2.3 × 10-1
Question 59 |
Consider a quadratic equation x2 - 13x + 36 = 0 with coefficients in a base b. The solutions of this equation in the same base b are x = 5 and x = 6. Then b=________.
8 | |
9 | |
10 | |
11 |
Generally if a, b are roots.
(x - a)(x - b) = 0
x2 - (a + b)x + ab = 0
Given that x=5, x=6 are roots of (1)
So, a + b = 13
ab=36 (with same base ‘b’)
i.e., (5)b + (6)b = (13)b
Convert them into decimal value
5b = 510
610 = 610
13b = b+3
11 = b+3
b = 8
Now check with ab = 36
5b × 6b = 36b
Convert them into decimals
5b × 6b = (b×3) + 610
30 = b × 3 + 6
24 = b × 3
b = 8
∴ The required base = 8
Question 60 |
Consider a binary code that consists of only four valid code words as given below:
Let the minimum Hamming distance of the code be p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are
p=3 and q=1 | |
p=3 and q=2 | |
p=4 and q=1 | |
p=4 and q=2 |
Minimum Distance = p = 3

Error bits that can be corrected = (p-1)/2 = (3-1)/2 = 1
∴ p=3 and q=1
Question 61 |
The n-bit fixed-point representation of an unsigned real number X uses f bits for the fraction part. Let i = n-f. The range of decimal values for X in this representation is
2-f to 2i | |
2-f to (2i - 2-f) | |
0 to 2i | |
0 to (2i - 2-f ) |
Number of bits in fraction part → f-bits
Number of bits in integer part → (n – f) bits
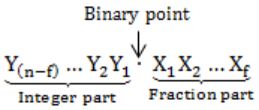
Minimum value:
000…0.000…0 = 0
Maximum value:
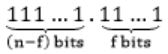
= (2 n-f - 1) + (1 - 2 -f
= (2n-f - 2 -f)
= (2i - 2 -f )
Question 62 |
The base (or radix) of the number system such that the following equation holds is_________.
312/20 = 13.1
5 | |
6 | |
7 | |
8 |
(3r2 + r + 2) / 2r= (r+3+1/r)
(3r2 + r + 2) / 2r= (r2+3r+1) / r
(3r2 + r + 2) = (2r2+6r+2)
r2 -5r = 0
Therefor r = 5
Question 63 |
In the IEEE floating point representation, the hexadecimal value 0×00000000 corresponds to
the normalized value 2 - 127 | |
the normalized value 2 - 126 | |
the normalized value + 0 | |
the special value + 0 |

Question 64 |
Let r denote number system radix. The only value(s) of r that satisfy the equation ![]() is/are
is/are
decimal 10 | |
decimal 11 | |
decimal 10 and 11 | |
any value > 2 |
(r2 + 2r + 1)1/2 = r + 1
(r + 1)2 * 1/2 = r + 1
r + 1 = r + 1 Any value of r will satisfy the above equation. But the radix should be greater than 2 because the 121 has 2. So r > 2 is correct.
Question 65 |
P is a 16-bit signed integer. The 2's complement representation of P is (F87B)16. The 2's complement representation of 8*P is
(C3D8)16 | |
(187B)16 | |
(F878)16 | |
(987B)16 |
(F87B)16=(1111 1000 0111 1011)2. (It is a negative number which is in 2's complement form)
P = 1111 1000 0111 1011 (2's complement form)
8 * P = 23* P = 1100 0011 1101 1000. ( NOTE: Left shift k times is equivalent to Multiplication by 2k)
Hence, 1100 0011 1101 1000 is 2's complement representation of 8P.
1100 0011 1101 1000 = (C3D8)16.
Question 66 |
Consider the equation (123)5 = (x8)y with x and y as unknown. The number of possible solutions is __________.
3 | |
5 | |
6 | |
7 |
(123)5 = (x8)y
In R.H.S. since y is base so y should be greater than x and 8, i.e.,
y > x
y > 8
Now, to solve let's change all the above bases number into base 10 number,
52 × 1 +2 × 5 + 3 = y × x + 8
38 = xy + 8
xy = 30
⇒ yx = 30
So the possible combinations are
(1,30), (2,15), (3,10), (5,6)
But we will reject (5,6) because it violates the condition (y > 8).
So, total solutions possible is 3.
