digital-logic-design
Question 1 |
A | exponent = 00000001 and mantissa = 00000000000000000000001 |
B | exponent = 00000001 and mantissa = 00000000000000000000000 |
C | exponent = 00000000 and mantissa = 00000000000000000000000 |
D | exponent = 00000000 and mantissa = 00000000000000000000001 |
The smallest biased exponent for the normalized number is E= 1.
The smallest Mantissa M = 000...0
The smallest positive normalized number = 1.M x 2 E-127
= 1.0 x 2 -126 .
= 2 -126
Question 2 |
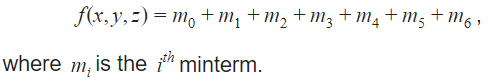
A |  |
B |  |
C |  |
D |  |
E |

Question 3 |
A | 0x4243 |
B | 0x6665 |
C | 0x0001 |
D | 0x0100 |
It is given that the unsigned integer is 2-bytes long. It needs 4 hexadecimal digits.
We know the big-endian and little-endian computers differ in how the data is stored in memory.
In little endian machines, the last byte of binary representation of the multibyte data-type is stored first. On the other hand, in big endian machines, the first byte of binary representation of the multibyte data-type is stored first.
In the hexadecimal representation of the 2-byte number on the little endian machine, the first two hexadecimal digits are for one byte and the last two hexadecimal digits are for the second byte. On the big endian machine it is the other way round.
It is given that the value in little endian representation is 255 more than the value in the big endian machine.
From the given options
A). In little endian = 0x4243 in binary (0100 0010 0100 0011) which has decimal value = 16963
On big endian = 0x4342 in binary (0100 0011 0100 0010) which has decimal value = 17218
Here the big endian value is higher than the little endian value. So this is not the correct option.
B). In little endian 0x6665 in binary (0110 0110 0110 0101) which has the decimal value = 26213
In big endian 0x6566 in binary (0110 0101 0110 0110) which has the decimal value = 25958
The difference = 26213 - 25958 = 255. So this is also the correct option.
C). In little endian 0x0001 in binary (0000 0000 0000 0001) which has the decimal value = 1.
In big endian 0x0100 in binary (0000 0001 0000 0000) has decimal value = 256.
But here also the big endian value is higher than the little endian. So this is not the correct option.
D). On the little endian machine for hexadecimal number 0x0100 in binary (0000 0001 0000 0000) which has decimal value = 256. On a big endian machine it is 0x 0001 in binary (0000 0000 0000 0001) which has decimal value = 1
The difference in value of little endian to big endian is 256-1 = 255.
Hence 2, 4 are the correct options.
Question 4 |
f(w, 0, 0, z) = 1
f(1, x, 1, z) = x + z
f(w, 1, y, z) = wz + y
The number of literals in the minimal sum-of-products expression of f is __________.
A | 6 |
f(w,0,0,z)= 1 If x=y=0, then the sum of the corresponding minterms be 1.
The minterms with literals x’ and y’ are wx’y’z(9), w’x’y’z(1), wx’y’z’(8), w’x’y’z’(0) .
If x=y=0, then we get wz+w’z+wz’+w’z’ = 1.
f(1,x,1,z)= x+z.
The minterms with variables w and y in true form and x or z or both in true form.
The corresponding minterms are wx’yz(11), wxyz’(14), wxyz(15)
If w=1 and y=1, then we get x’z+xz’+xz= x+z.
f(w,1,y,z)= wz+y
The corresponding minterms are w’xyz’(6), w’xyz(7), wxyz’(14), wxyz(15), wxy’z(13).
If x=1, then we get w’yz’ + w’yz+ wyz’ + wyz+ wy’z = y + wz
So, the function f(w,x,y,z)= Σ(0,1,6,7, 8,9, 11, 13, 14, 15,).
Therefore, the k-map will be:
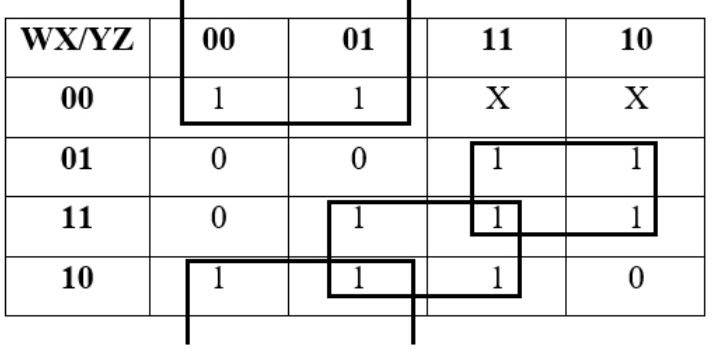
Therefore, the minimal expression will be: X’Y’ + WZ + XY
Thus, the number of literals will be 6.
Question 5 |
A | 3 |
x=1 and y=2
x+y= 1+2=3
Question 6 |
What values of A, B, C and D satisfy the following simultaneous Boolean equations?
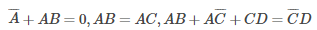
A | A = 1, B = 0, C = 0, D = 1 |
B | A = 1, B = 1, C = 0, D = 0 |
C | A = 1, B = 0, C = 1, D = 1 |
D | A = 1, B = 0, C = 0, D = 0 |
Question 7 |
The number of 1’s in the binary representation of
(3*4096 + 15*256 + 5*16 + 3) are:
A | 8 |
B | 8 |
C | 10 |
D | 12 |
= (11000000000000)2
15 × 256 = 15 × 28
= (111100000000)2
5 × 16 = 5 × 24
= (1010000)2
3 = (11)2
Hence, all binary numbers,

∴ 101's
Question 8 |
(a) Implement a circuit having the following output expression using an inverter and NAND gate ![]() .
.
(b) What is the equivalent minimal Boolean expression (in sum of products form)
for the Karnaugh map given below?
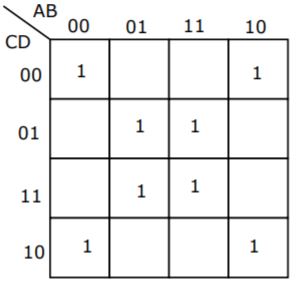
A | Theory Explanation. |
Question 9 |
(a) An asynchronous serial communication controller that uses a start stop scheme for controlling the serial I/O of a system is programmed for a string of length seven bits, one parity bit (odd parity) and one step bit. The
transmission rate is 1200 bits/second.
(i) What is the complete bit stream that is transmitted for the string ‘0110101’?
(ii) How many such strings can be transmitted per second?
(b) Consider a CRT display that has a text mode display format of 80 × 25 characters with a 9 × 12 character cell. What is the size of the video buffer RAM for the display to be used in monochrome (1 bit per pixel) graphics mode?
A | Theory Explanation. |
Question 10 |
A multiplexer is placed between a group of 32 registers and an accumulator to regulate data movement such that at any given point in time the content of only one register will move to the accumulator. The minimum number of select lines needed for the multiplexer is _____.
A | 5 |
A 25x1 Multiplexer with 5 select lines selects one of the 32(= 25) registers at a time depending on the selection input.
The content from the selected register will be transferred through the output line to the Accumulator.
Question 11 |
If there are m input lines and n output lines for a decoder that is used to uniquely address a byte addressable 1 KB RAM, then the minimum value of m + n is ____.
A | 1034 |
Each output line of the decoder is connected to one of the 1K(= 1024) rows of RAM.
Each row stores 1 Byte.
m=10 and n=1024
Question 12 |
Consider the Boolean function z(a,b,c).

Which one of the following minterm lists represents the circuit given above?
A | Z = ∑(0,1,3,7) |
B | Z = ∑(2,4,5,6,7) |
C | Z = ∑(1,4,5,6,7) |
D | Z = ∑(2,3,5) |
Convert a+b’c into canonical form which is sum of minterms.
a + b’c = a(b + b’)(c + c’) + (a + a’)b’c
= abc + abc’ + ab’c + ab’c’ + ab’c + a’b’c
= Σ(7,6,5,4,1)
Question 13 |
Consider three registers R1, R2 and R3 that store numbers in IEEE-754 single precision floating point format. Assume that R1 and R2 contain the values (in hexadecimal notation) 0x42200000 and 0xC1200000, respectively.
If R3 = R1/R2, what is the value stored in R3?
A | 0x40800000 |
B | 0x83400000 |
C | 0xC8500000 |
D | 0xC0800000 |

R1 = 1.0100..0 X 2132-127
= 1.0100..0 X 25
= 101.0 X 23
= 5 X 8
= 40

R2 = (-1) x 1.0100..0 X 2130-127
= (-1) x 1.0100..0 X 23
= (-1) x 101.0 X 21
= (-1) x5 X 2
= -10
R3 = R1/R2
= -4
= (-1)x 1.0 x 22
Sign = 1
Mantissa = 000..0
Exponent = 2+127 = 129

R3 = 1100 0000 1000 000..0
= 0x C 0 8 0 0 0 0 0
Question 14 |
A ROM is sued to store the table for multiplication of two 8-bit unsigned integers. The size of ROM required is
A | 256 × 16 |
B | 64 K × 8 |
C | 4 K × 16 |
D | 64 K × 16 |
No. of results possible = 28 × 28 = 216 = 64K
Then total size of ROM = 64K × 16
Question 15 |
Both’s algorithm for integer multiplication gives worst performance when the multiplier pattern is
A | 101010 …..1010 |
B | 100000 …..0001 |
C | 111111 …..1111 |
D | 011111 …..1110 |
Question 16 |
Consider the following floating point number representation

The exponent is in 2's complement representation and mantissa is in the sign magnitude representation. The range of the magnitude of the normalized numbers in this representation is
A | 0 to 1 |
B | 0.5 to 1 |
C | 2-23 to 0.5 |
D | 0.5 to (1-2-23) |
Question 17 |
Consider the circuit given below which has a four bit binary number b3b2b1b0 as input and a five bit binary number d4d3d2d1d0 as output. The circuit implements:

A | Binary of Hex conversion
|
B | Binary to BCD conversion |
C | Binary to grey code conversion |
D | Binary to radix-12 conversion |
Whenever, b2 = b3 = 1, then only 0100, i.e., 4 is added to the given binary number. Lets write all possibilities for b.
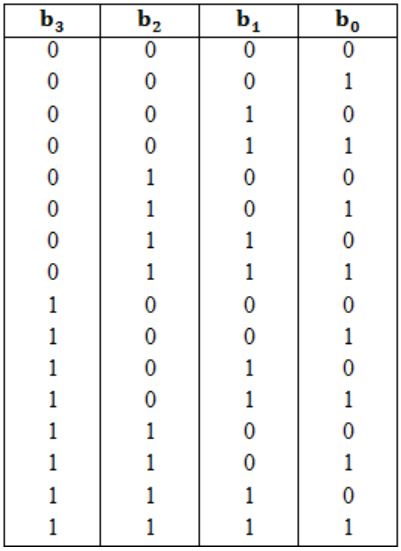
Note that the last 4 combinations leads to b3 and b2 as 1. So, in these combinations only 0010 will be added.
1100 is 12
1101 is 13
1110 is 14
1111 is 15
in binary unsigned number system.
1100 + 0100 = 10000
1101 + 0100 = 10001, and so on.
This is conversion to radix 12.
Question 18 |
Consider the circuit in below figure. f implements
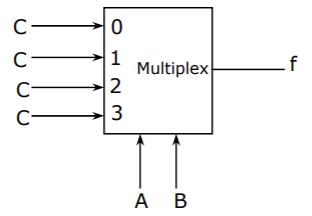
A |  |
B | A + B + C |
C | A ⊕ B ⊕ C |
D | AB + BC + CA |
Question 19 |
What is the equivalent Boolean expression in product-of-sums form for the Karnaugh map given below.
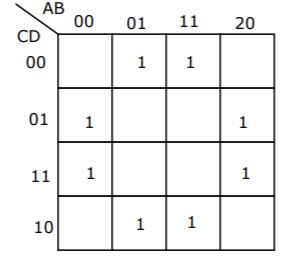
A | 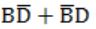 |
B | 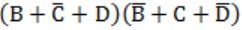 |
C | 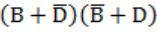 |
D |  |
E | None of the above |
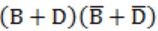

Question 20 |
A logic network has two data inputs A and B, and two control inputs C0 and C1. It implements the function F according to the following table.

Implement the circuit using one 4 to 1 Multiplexer, one 2-input Exclusive OR gate, one 2-input AND gate, one 2-input OR gate and one Inverter.
A | Theory Explanation. |
Question 21 |
Consider the synchronous sequential circuit in the below figure.

(a) Draw a state diagram, which is implemented by the circuit. Use the following names for the states corresponding to the values of flip-flops as given below.
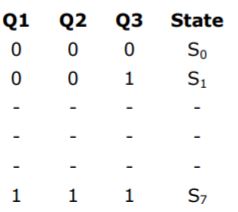
(b) Given that the initial state of the circuit is S4, identify the set of states, which are not reachable.
A | Theory Explanation. |
Question 22 |
Let * be defined as x * y = x' + y. Let z = x * y. Value of z * x is
A | x'+y |
B | x |
C | 0 |
D | 1 |
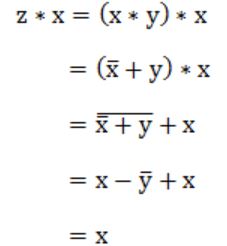
Question 23 |
An N-bit carry look ahead adder, where N is a multiple of 4, employs ICs 74181 (4 bit ALU) and 74182 (4 bit carry look ahead generator).
The minimum addition time using the best architecture for this adder is
A | proportional to N |
B | proportional to log N |
C | a constant |
D | None of the above |
Question 24 |
Let f(x, y, z) = x' + y'x + xz be a switching function. Which one of the following is valid?
A |  |
B | xz is a minterm of f |
C | xz is an implicant of f |
D | y is a prime implicant of f |
Question 25 |
Given √224)r = 13)r.
The value of the radix r is:
A | 10 |
B | 8 |
C | 5 |
D | 6 |
Convert r base to decimal.
√2r2 + 25 + 4 = r + 3
Take square both sides,
2r2 + 2r + 4 = r2 + 6r + 9
r2 - 4r - 5 = 0
r2 - 5r + r - 5 = 0
r(r - 5) + (r - 5) = 0
r = -1, 5
r cannot be -1,
So r = 5 is correct answer.
Question 26 |
Consider a logic circuit shown in figure below. The functions f1, f2 and f (in canonical sum of products form in decimal notation) are:
f1(w,x,y,z) = ∑8,9,10 f2(w,x,y,z) = ∑7,8,12,13,14,15 f(w,x,y,z) = ∑8,9
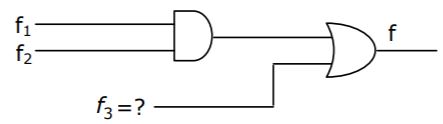
The function f3 is
A | Σ9,10 |
B | Σ9 |
C | Σ1,8,9 |
D | Σ8,10,15 |
Since, f1 and f2 are in canonical sum of products form, f1⋅f2 will only contain their common terms that is f1⋅f2 = Σ8.
Now,
Σ8 + f3 = Σ8,9
So, f3= Σ9
Question 27 |
Let ⊕ and ⊙ denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT?
A | 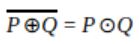 |
B | 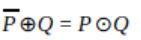 |
C | 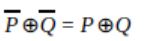 |
D |  |

Question 28 |
Consider the sequential circuit shown in the figure, where both flip-flops used are positive edge-triggered D flip-flops.

The number of states in the state transition diagram of this circuit that have a transition back to the same state on some value of "in" is ______
A | 2 |
B | 3 |
C | 4 |
D | 5 |

Now lets draw characteristic table,
D1 = Q0
D0 = in

Question 29 |
b7 b6 b5 b4 b3 b2 b1 b0
where the position of the binary point is between b3 and b2 . Assume b7 is the most significant bit.
Some of the decimal numbers listed below cannot be represented exactly in the above representation:
(i) 31.500
(ii) 0.875
(iii) 12.100
(iv) 3.001
Which one of the following statements is true?
A | None of (i), (ii), (iii), (iv) can be exactly represented
|
B | Only (ii) cannot be exactly represented |
C | Only (iii) and (iv) cannot be exactly represented |
D | Only (i) and (ii) cannot be exactly represented |
= 16 + 8 + 4 + 2 + 1 + 0.5
= (31.5)10
(ii) (0.875)10 = (00000.111)2
= 2-1 + 2-2 + 2-3
= 0.5 + 0.25 + 0.125
= (0.875)10
(iii) (12.100)10
It is not possible to represent (12.100)10
(iv) (3.001)10 It is not possible to represent (3.001)10
Question 30 |
Consider the minterm list form of a Boolean function F given below.
- F(P, Q, R, S) = Σm(0, 2, 5, 7, 9, 11) + d(3, 8, 10, 12, 14)
Here, m denotes a minterm and d denotes a don’t care term. The number of essential prime implicants of the function F is _______.
A | 3 |
B | 4 |
C | 5 |
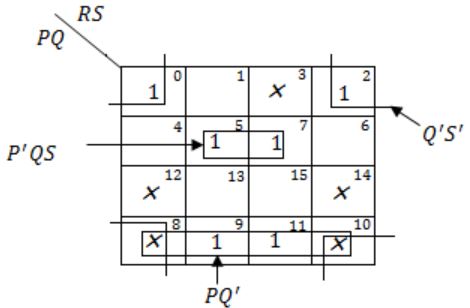
There are 3 prime implicant i.e., P’QS, Q’S’ and PQ’ and all are essential.
Because 0 and 2 are correct by only Q’S’, 5 and 7 are covered by only P’QS and 8 and 9 are covered by only PQ’.
Question 31 |
What happens when a bit-string is XORed with itself n-times as shown:
[B⊕(B⊕(B⊕(B........ n times)]
A | complements when n is even |
B | complements when n is odd |
C | divides by 2n always |
D | remains unchanged when n is even |
Consider:
B⊕(B⊕B)
= B⊕0
= 0 (if consider n times it remains unchanged)
Question 32 |
A multiplexor with a 4 bit data select input is a
A | 4:1 multiplexor |
B | 2:1 multiplexor |
C | 16:1 multiplexor |
D | 8:1 multiplexor |
For 4 bit data it selects 24 : 1 = 16: 1 input
Question 33 |
The threshold level for logic 1 in the TTL family is
A | any voltage above 2.5 V |
B | any voltage between 0.8 V and 5.0 V |
C | any voltage below 5.0 V |
D | any voltage below Vcc but above 2.8 V |
Question 34 |
The octal representation of an integer is (342)8. If this were to be treated as an eight-bit integer is an 8085 based computer, its decimal equivalent is
A | 226 |
B | -98 |
C | 76 |
D | -30 |
If this can be treated as 8 bit integer, then the first becomes sign bit i.e., '1' then the number is negative.
8085 uses 2's complement then
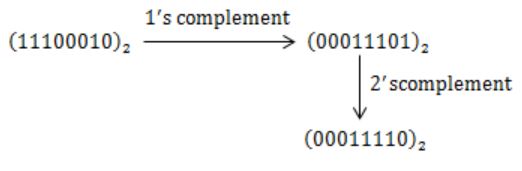
⇒ -30
Question 35 |
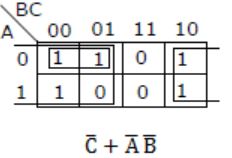
The function represented by the Karnaugh map given below is:
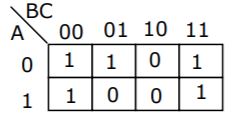
A | A⋅B |
B | AB+BC+CA |
C |  |
D | None of the above |
Question 36 |
Which of the following operations is commutative but not associative?
A | AND |
B | OR |
C | NAND |
D | EXOR |
Question 37 |
Suppose the domain set of an attribute consists of signed four digit numbers. What is the percentage of reduction in storage space of this attribute if it is stored as an integer rather than in character form?
A | 80% |
B | 20% |
C | 60% |
D | 40% |
We have four digits. So to represent signed 4 digit numbers we need 5 bytes, 4 bytes for four digits and 1 for the sign.
So required memory = 5 bytes.
Now, if we use integer, the largest no. needed to represent is 9999 and this requires 2 bytes of memory for signed representation.
9999 in binary requires 14 bits. So, 2 bits remaining and 1 we can use for sign bit.
So, memory savings,
= 5 - 2/5 × 100
= 60%
Question 38 |
(a) The implication gate shown below, has two inputs (x and y), the output is 1 except when x=1 and y=0. Realize f = x'y + xy' using only four implication gates.

(b) Show that the implication gate is functionally complete.
A | Theory Explanation. |
Question 39 |
Design a synchronous counter to go through the following states:
1, 4, 2, 3, 1, 4, 2, 3, 1, 4,...........
A | Theory Explanation. |
Question 40 |
 ?
?A | x NAND X |
B | x NOR x |
C | x NAND 1 |
D | x NOR 1 |

Question 41 |
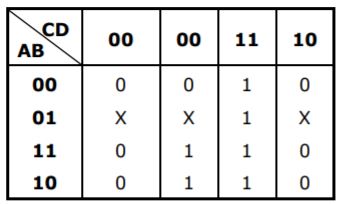
A | 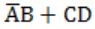 |
B |  |
C |  |
D | 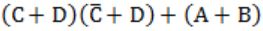 |

⇒ CD+AD = D(A+C)
Question 42 |
Booth’s coding in 8 bits for the decimal number –57 is
A | 0 – 100 + 1000 |
B | 0 – 100 + 100 - 1 |
C | 0 – 1 + 100 – 10 + 1 |
D | 00 – 10 + 100 - 1 |

Question 43 |
The maximum gate delay for any output to appear in an array multiplier for multiplying two n bit number is
A | On2 |
B | O(n) |
C | O(log n) |
D | O(1) |
Total delay = 1 * 2n - 1 = O(2n - 1) = n
Question 44 |
The number of full and half-adders required to add 16-bit numbers is
A | 8 half-adders, 8 full-adders |
B | 1 half-adder, 15 full-adders |
C | 16 half-adders, 0 full-adders |
D | 4 half-adders, 12 full-adders |
But for rest of bits we need full address since carry from previous addition has to be included into the addition operation.
So, in total 1 half adder and 15 full adders are required.
Question 45 |
Zero has two representations in
A | Sign magnitude |
B | 1’s complement |
C | 2’s complement |
D | None of the above |
E | Both A and B |
+0 = 0000
-0 = 1000
1's complement:
+0 = 0000
-0 = 1111
Question 46 |
The number 43 in 2’s complement representation is
A | 01010101 |
B | 11010101 |
C | 00101011 |
D | 10101011 |
Question 47 |
The simultaneous equations on the Boolean variables x, y, z and w,
x + y + z = 1
xy = 0
xz + w = 1
xy +  = 0
= 0
have the following solution for x, y, z and w, respectively.
A | 0 1 0 0 |
B | 1 1 0 1 |
C | 1 0 1 1 |
D | 1 0 0 0 |
Question 48 |
Which function does NOT implement the Karnaugh map given below?

A | (w + x)y |
B | xy + yw |
C | 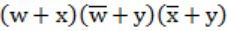 |
D | None of the above |
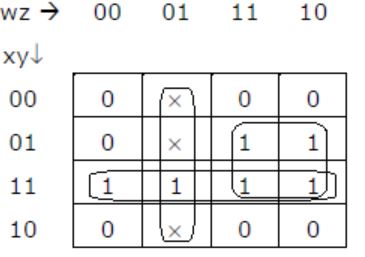
⇒ wy + wz + xy
Question 49 |
The following arrangement of master-slave flip flops
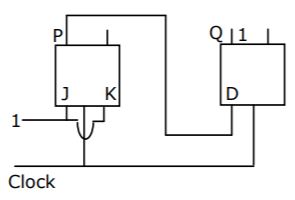
has the initial state of P, Q as 0, 1 (respectively). After three clock cycles the output state P, Q is (respectively),
A | 1, 0 |
B | 1, 1 |
C | 0, 0 |
D | 0, 1 |
When 11 is applied to Jk flip flop it toggles the value of P so op at P will be 1.
Input to D flip flop will be 0(initial value of P) so op at Q will be 0.
Question 50 |
Consider the values A = 2.0 x 1030, B = -2.0 x 1030, C = 1.0, and the sequence
X: = A + B Y: = A + C
X: = X + C Y: = Y + B
executed on a computer where floating-point numbers are represented with 32 bits. The values for X and Y will be
A | X = 1.0, Y = 1.0 |
B | X = 1.0, Y = 0.0 |
C | X = 0.0, Y = 1.0 |
D | X = 0.0, Y = 0.0 |
A = 2.0 * 1030, C = 1.0
So, A + C should make the 31st digit to 1, which is surely outside the precision level of A (it is 31st digit and not 31st bit). So, this addition will just return the value of A which will be assigned to Y.
So, Y + B will return 0.0 while X + C will return 1.0.
