UGC NET CS 2015 Dec- paper-2
Question 1 |
How many committees of five people can be chosen from 20 men and 12 women such that each committee contains at least three women?
75240 | |
52492 | |
41800 | |
9900 |
Question 1 Explanation:
Given data,
-- 20 men and 12 women
-- 5 people can choose from men and women
-- Each committee contains at least three women
Step-1: We have a constraint that each committee contains atleast 3 women.
possibility-1: 2 men + 3 women.
possibility-2: 1 men + 4 women.
possibility-3: 0 men + 5 women.
Step-1: They are asking to find all possibilities.
= (possibility -1)+ (possibility -2) + (possibility -3)
= . ( 20 C 2. * 12 C 3 ) + ( 20 C 2. * 12 C 2 ) + ( 20 C 2. * 12 C 2 )
= (190*220) + (20*495) + (1*792)
= 41800 + 9900 + 792
= 52492
-- 20 men and 12 women
-- 5 people can choose from men and women
-- Each committee contains at least three women
Step-1: We have a constraint that each committee contains atleast 3 women.
possibility-1: 2 men + 3 women.
possibility-2: 1 men + 4 women.
possibility-3: 0 men + 5 women.
Step-1: They are asking to find all possibilities.
= (possibility -1)+ (possibility -2) + (possibility -3)
= . ( 20 C 2. * 12 C 3 ) + ( 20 C 2. * 12 C 2 ) + ( 20 C 2. * 12 C 2 )
= (190*220) + (20*495) + (1*792)
= 41800 + 9900 + 792
= 52492
Question 2 |
Which of the following statement(s) is/are false ?
(a) A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.
(b) A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c) A complete graph (K n ) has a Hamilton Circuit whenever n ≥ 3.
(d) A cycle over six vertices (C 6 ) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
(a) A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.
(b) A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c) A complete graph (K n ) has a Hamilton Circuit whenever n ≥ 3.
(d) A cycle over six vertices (C 6 ) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
(a) only | |
(b) and (c) | |
(c) only | |
(d) only |
Question 2 Explanation:
(a)TRUE: A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.
(b)TRUE: A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c)TRUE: A complete graph (K n ) has a Hamilton Circuit whenever n ≥ 3. (d) FALSE: A cycle over six vertices (C 6 ) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
(b)TRUE: A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c)TRUE: A complete graph (K n ) has a Hamilton Circuit whenever n ≥ 3. (d) FALSE: A cycle over six vertices (C 6 ) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
Question 3 |
Which of the following is/are not true?
(a) The set of negative integers is countable.
(b) The set of integers that are multiples of 7 is countable.
(c)The set of even integers is countable.
(d)The set of real numbers between 0 and 1⁄2 is countable.
(a) The set of negative integers is countable.
(b) The set of integers that are multiples of 7 is countable.
(c)The set of even integers is countable.
(d)The set of real numbers between 0 and 1⁄2 is countable.
(a) and (c) | |
(b) and (d) | |
(b) only | |
(d) only |
Question 3 Explanation:
(a)TRUE: The set of negative integers is countable.
Suppose negative integers set size is 10.
Ex: -1, -2, -3,.....,-10 is countable
(b)TRUE: The set of integers that are multiples of 7 is countable.
Suppose set of integers size is 10.
Ex: 1*7, 2*7, 3*7, .....,10*7 is countable
(c)TRUE: The set of even integers is countable.
Suppose set of even integers size is 10.
Ex: 2,4,6,8,10,....,20
(d) FALSE: The set of real numbers between 0 and 1⁄2 is countable. We can’t count real numbers.
Ex: 0.1, 0.2, 0.3, .....,0.∞
Suppose negative integers set size is 10.
Ex: -1, -2, -3,.....,-10 is countable
(b)TRUE: The set of integers that are multiples of 7 is countable.
Suppose set of integers size is 10.
Ex: 1*7, 2*7, 3*7, .....,10*7 is countable
(c)TRUE: The set of even integers is countable.
Suppose set of even integers size is 10.
Ex: 2,4,6,8,10,....,20
(d) FALSE: The set of real numbers between 0 and 1⁄2 is countable. We can’t count real numbers.
Ex: 0.1, 0.2, 0.3, .....,0.∞
Question 4 |
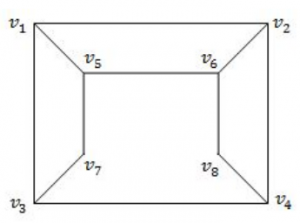
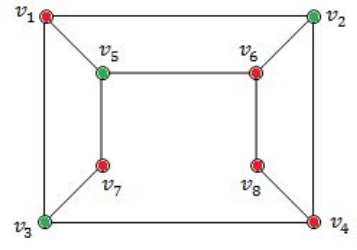
Consider the graph given below: The two distinct sets of vertices, which make the graph bipartite are:
(v 1 , v 4 , v 6 ); (v 2 , v 3 , v 5 , v 7 , v 8 ) | |
(v 1 , v 7 , v 8 ); (v 2 , v 3 , v 5 , v 6 ) | |
(v 1 , v 4 , v 6 , v 7 ); (v 2 , v 3 , v 5 , v 8 ) | |
(v 1 , v 4 , v 6 , v 7 , v 8 ); (v 2 , v 3 , v 5 ) |
Question 4 Explanation:
A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
→ The two sets U and V may be thought of as a coloring of the graph with two colors.
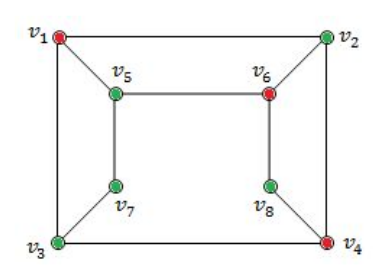
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.

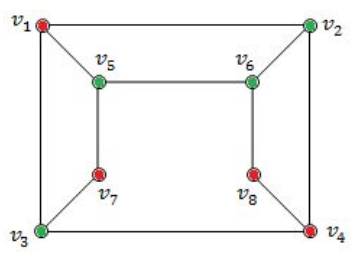
Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.

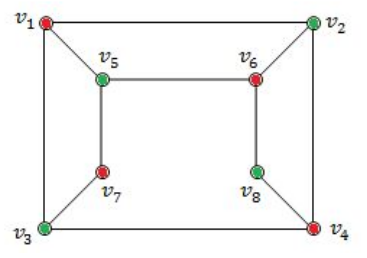
Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.

Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.

→ The two sets U and V may be thought of as a coloring of the graph with two colors.
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.
Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.
Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.
Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.
Question 5 |
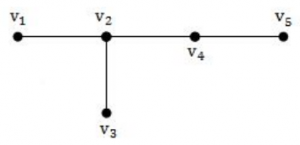
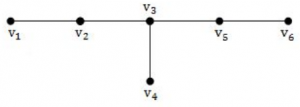
A tree with n vertices is called graceful, if its vertices can be labelled with integers 1, 2,....n such that the absolute value of the difference of the labels of adjacent vertices are all different. Which of the following trees are graceful?
(a)
(b)
(c)
(a)

(b)
(c)
(a) and (b) | |
(b) and (c) | |
(a) and (c) | |
(a), (b) and (c) |
Question 5 Explanation:
Above all graphs are graceful.


Question 6 |
Which of the following arguments are not valid ?
(a) “If Gora gets the job and works hard, then he will be promoted. If Gora gets promotion, then he will be happy. He will not be happy, therefore, either he will not get the job or he will not work hard”.
(b) “Either Puneet is not guilty or Pankaj is telling the truth. Pankaj is not telling the truth, therefore, Puneet is not guilty”.
(c) If n is a real number such that n >1, then n 2 >1. Suppose that n 2 >1, then n >1.
(a) “If Gora gets the job and works hard, then he will be promoted. If Gora gets promotion, then he will be happy. He will not be happy, therefore, either he will not get the job or he will not work hard”.
(b) “Either Puneet is not guilty or Pankaj is telling the truth. Pankaj is not telling the truth, therefore, Puneet is not guilty”.
(c) If n is a real number such that n >1, then n 2 >1. Suppose that n 2 >1, then n >1.
(a) and (c) | |
(b) and (c) | |
(a), (b) and (c) | |
(a) and (b) |
Question 7 |
Let P(m, n) be the statement “m divides n” where the Universe of discourse for both the variables is the set of positive integers. Determine the truth values of the following propositions.
(a)∃m ∀n P(m, n)
(b)∀n P(1, n)
(c) ∀m ∀n P(m, n)
(a)∃m ∀n P(m, n)
(b)∀n P(1, n)
(c) ∀m ∀n P(m, n)
(a) - True; (b) - True; (c) - False | |
(a) - True; (b) - False; (c) - False | |
(a) - False; (b) - False; (c) - False | |
(a) - True; (b) - True; (c) - True |
Question 7 Explanation:
Given P(m,n) ="m divides n"
Statement-A is ∃m ∀n P(m, n). Here, there exists some positive integer which divides every positive integer. It is true because there is positive integer 1 which divides every positive integer.
Statement-B is ∀n P(1, n). Here, 1 divided every positive integer. It is true.
Statement-C is ∀m ∀n P(m, n). Here, every positive integer divided every positive integer. It is false.
Statement-A is ∃m ∀n P(m, n). Here, there exists some positive integer which divides every positive integer. It is true because there is positive integer 1 which divides every positive integer.
Statement-B is ∀n P(1, n). Here, 1 divided every positive integer. It is true.
Statement-C is ∀m ∀n P(m, n). Here, every positive integer divided every positive integer. It is false.
Question 8 |
Match the following terms:


(i)(ii)(iii)(iv) | |
(ii)(iii)(i)(iv) | |
(iii)(ii)(iv)(i) | |
(iv)(iii)(ii)(i) |
Question 8 Explanation:
→ Vacuous proof is a proof that the implication p → q is true based on the fact that p is false.
→ Trivial proof is a proof that the implication p → q is true based on the fact that q is true.
→ Direct proof is a proof that the implication p → q is true that proceeds by showing that q must be true when p is true.
→ Indirect proof is a proof that the implication p → q is true that proceeds by showing that p must be false when q is false.
→ Trivial proof is a proof that the implication p → q is true based on the fact that q is true.
→ Direct proof is a proof that the implication p → q is true that proceeds by showing that q must be true when p is true.
→ Indirect proof is a proof that the implication p → q is true that proceeds by showing that p must be false when q is false.
Question 9 |
Consider the compound propositions given below as:
(a)p ∨ ~(p ∧ q)
(b)(p ∧ ~q) ∨ ~(p ∧ q)
(c)p ∧ (q ∨ r)
Which of the above propositions are tautologies?
(a)p ∨ ~(p ∧ q)
(b)(p ∧ ~q) ∨ ~(p ∧ q)
(c)p ∧ (q ∨ r)
Which of the above propositions are tautologies?
(a) and (c) | |
(b) and (c) | |
(a) and (b) | |
only (a) |
Question 9 Explanation:
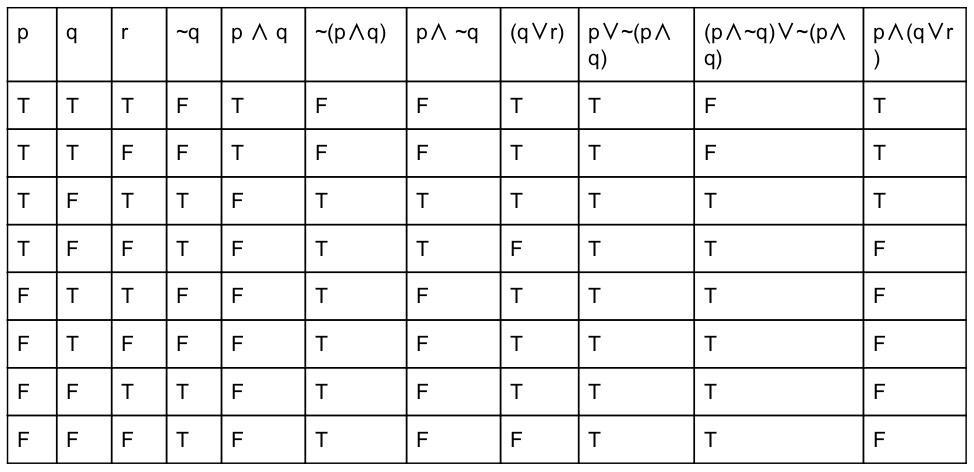
Question 10 |
Which of the following property/ies a Group G must hold, in order to be an Abelian group?
(a)The distributive property
(b)The commutative property
(c)The symmetric property
(a)The distributive property
(b)The commutative property
(c)The symmetric property
(a) and (b) | |
(b) and (c) | |
(a) only | |
(b) only |
Question 10 Explanation:
An abelian group is a set, A, together with an operation • that combines any two elements a and b to form another element denoted a • b. The symbol • is a general placeholder for a
concretely given operation. To qualify as an abelian group, the set and operation, (A, •), must satisfy five requirements known as the abelian group axioms:
Closure: For all a, b in A, the result of the operation a • b is also in A.
Associativity: For all a, b and c in A, the equation (a • b) • c = a • (b • c) holds.
Identity element: There exists an element e in A, such that for all elements a in A, the equation e • a = a • e = a holds.
Inverse element: For each a in A, there exists an element b in A such that a • b = b • a = e, where e is the identity element.
Commutativity: For all a, b in A, a • b = b • a.
A group in which the group operation is not commutative is called a "non-abelian group" or "non-commutative group".
Closure: For all a, b in A, the result of the operation a • b is also in A.
Associativity: For all a, b and c in A, the equation (a • b) • c = a • (b • c) holds.
Identity element: There exists an element e in A, such that for all elements a in A, the equation e • a = a • e = a holds.
Inverse element: For each a in A, there exists an element b in A such that a • b = b • a = e, where e is the identity element.
Commutativity: For all a, b in A, a • b = b • a.
A group in which the group operation is not commutative is called a "non-abelian group" or "non-commutative group".
Question 11 |
Consider the following program :
#include
main( )
{
int i, inp;
float x, term=1, sum=0;
scanf(“%d %f ”, &inp, &x);
for(i=1; i<=inp; i++)
{
term = term * x/i;
sum = sum + term ;
}
printf(“Result = %f\n”, sum);
}
The program computes the sum of which of the following series?
#include
main( )
{
int i, inp;
float x, term=1, sum=0;
scanf(“%d %f ”, &inp, &x);
for(i=1; i<=inp; i++)
{
term = term * x/i;
sum = sum + term ;
}
printf(“Result = %f\n”, sum);
}
The program computes the sum of which of the following series?
x + x 2 /2 + x 3 /3 + x 4 /4 +... | |
x + x 2 /2! + x 3 /3! + x 4 /4! +... | |
1 + x 2 /2 + x 3 /3 + x 4 /4 +... | |
1 + x 2 /2! + x 3 /3! + x 4 /4! +... |
Question 11 Explanation:
In this problem, we have to find series of evaluation.
Let x=5, inp=5
Iteration-1:
for(i=1; i<=inp; i++)
/* condition true 1<=5 */
{
term = term * x/i;
/* (1*5)/1=5. Here, 5 nothing but ‘x’ */
sum = sum + term ; /* 0+5=5 */
}
Iteration-2: Here, ‘i’ becomes 2.
for(i=2; i<=inp; i++)
/* condition true 2<=5 */
{
term = term * x/i;
/* (5*5)/2 is nothing but x 2 /i */
sum = sum + term ; /* 5+12=17 */
}
;;;
;;;
Iteration-5: Here, ‘i’ becomes 5.
for(i=5; i<=inp; i++)
/* condition true 5<=5 */
{
term = term * x/i;
/* (625*5)/5! is nothing but x 5 /i! */
sum = sum + term ;
}
So, Option-B is correct answer.
Let x=5, inp=5
Iteration-1:
for(i=1; i<=inp; i++)
/* condition true 1<=5 */
{
term = term * x/i;
/* (1*5)/1=5. Here, 5 nothing but ‘x’ */
sum = sum + term ; /* 0+5=5 */
}
Iteration-2: Here, ‘i’ becomes 2.
for(i=2; i<=inp; i++)
/* condition true 2<=5 */
{
term = term * x/i;
/* (5*5)/2 is nothing but x 2 /i */
sum = sum + term ; /* 5+12=17 */
}
;;;
;;;
Iteration-5: Here, ‘i’ becomes 5.
for(i=5; i<=inp; i++)
/* condition true 5<=5 */
{
term = term * x/i;
/* (625*5)/5! is nothing but x 5 /i! */
sum = sum + term ;
}
So, Option-B is correct answer.
Question 12 |
Consider the following two statements:
(a) A publicly derived class is a subtype of its base class.
(b) Inheritance provides for code reuse.
(a) A publicly derived class is a subtype of its base class.
(b) Inheritance provides for code reuse.
Both the statements (a) and (b) are correct. | |
Neither of the statements (a) and (b) are correct | |
Statement (a) is correct and (b) is incorrect | |
Statement (a) is incorrect and (b) is correct. |
Question 12 Explanation:
→ A publicly derived class is a subtype of its base class.
→ Inheritance is defined as deriving new classes (sub classes) from existing ones (super class or base class) and forming them into a hierarchy of classes.
→ Inheritance allows programmers to create classes that are built upon existing classes, to specify a new implementation while maintaining the same behaviors (realizing an interface), to reuse code and to independently extend original software via public classes and interfaces.
→ Inheritance is defined as deriving new classes (sub classes) from existing ones (super class or base class) and forming them into a hierarchy of classes.
→ Inheritance allows programmers to create classes that are built upon existing classes, to specify a new implementation while maintaining the same behaviors (realizing an interface), to reuse code and to independently extend original software via public classes and interfaces.
There are 12 questions to complete.
