![GATE 2014 [Set-1]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png){kind=logo}
GATE 2014 [Set-1]
Question 1 |
Which of the following options is the closest in meaning to the phrase underlined in the sentence below? It is fascinating to see life forms cope with varied environmental conditions.
adopt to | |
adapt to | |
adept in | |
accept with |
(1) Adopt ⇒ Legally take and bring it up as one's own.
(2) Adapt ⇒ Make suitable for a new use or purpose.
(3) Adept ⇒ Very skilled (or) proficienct at something.
(4) Accept ⇒ Believe (or) come to recognize as valid (or) correct.
Option B is correct.
Question 2 |
Choose the most appropriate word from the options given below to complete the following sentence. He could not understand the judges awarding her the first prize, because he thought that her performance was quite __________.
superb | |
medium | |
mediocre | |
exhilarating |
Question 3 |
In a press meet on the recent scam, the minister said, "The buck stops here". What did the minister convey by the statement?
He wants all the money | |
He will return the money | |
He will assume final responsibility | |
He will resist all enquiries |
⇒ It represents that this is the final stage of responsibility.
Question 4 |
If (z + 1/z)2 = 98, compute (z2+ 1/z2).
96 | |
97 | |
98 | |
99 |
= 98
⇒ z2 + 1/z2
= 96
Question 5 |
The roots of ax2 + bx + c = 0 are real and positive. a, b and c are real. Then ax2 + b|x|+ c = 0 has
no roots | |
2 real roots | |
3 real roots | |
4 real roots |
For roots to be real & positive b2-4ac>0
This will have 2 real positive roots.
ax2+b|x|+c = 0
Discriminant = b2-4ac>0
ax2+bx+c
(-b)2-4ac
⇒ b2-4ac
Is also > 0. This will have real roots.
⇒ This will have 4 real roots.
Question 6 |
The Palghat Gap (or Palakkad Gap), a region about 30 km wide in the southern part of the Western Ghats in India, is lower than the hilly terrain to its north and south. The exact reasons for the formation of this gap are not clear. It results in the neighbouring regions of Tamil Nadu getting more rainfall from the South West monsoon and the neighbouring regions of Kerala having higher summer temperatures. What can be inferred from this passage?
The Palghat gap is caused by high rainfall and high temperatures in southern Tamil Nadu and Kerala | |
The regions in Tamil Nadu and Kerala that are near the Palghat Gap are low-lying | |
The low terrain of the Palghat Gap has a significant impact on weather patterns in neighbouring parts of Tamil Nadu and Kerala | |
Higher summer temperatures result in higher rainfall near the Palghat Gap area |
⇒ Option C is suitable option.
Question 7 |
Geneticists say that they are very close to confirming the genetic roots of psychiatric illnesses such as depression and schizophrenia, and consequently, that doctors will be able to eradicate these diseases through early identification and gene therapy. On which of the following assumptions does the statement above rely?
Strategies are now available for eliminating psychiatric illnesses | |
Certain psychiatric illnesses have a genetic basis | |
All human diseases can be traced back to genes and how they are expressed | |
In the future, genetics will become the only relevant field for identifying psychiatric illnesses |
⇒ Option B is the only option that contain illness.
Question 8 |
Round-trip tickets to a tourist destination are eligible for a discount of 10% on the total fare. In addition, groups of 4 or more get a discount of 5% on the total fare. If the one way single person fare is Rs 100, a group of 5 tourists purchasing round-trip tickets will be charged Rs _________.
850 | |
851 | |
852 | |
853 |
Round trip, there is a discount of 10% of total fare.
Group of 4 or more, Discount of 5% of total fare.
∴ 5 tourists ⇒ Total fare = 5 × 200 = 1000
Total discount = 10% of 1000 + 5% of 1000
= 100 + 50
= ₹150
∴ Fare charged = 1000 - 150 = ₹850
Question 9 |
In a survey, 300 respondents were asked whether they own a vehicle or not. If yes, they were further asked to mention whether they own a car or scooter or both. The irresponses are tabulated below. What percent of respondents do not own a scooter?
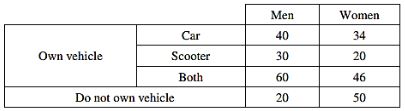
48 | |
49 | |
50 | |
51 |
[No. of respondents who do not own a scooter] = [No. of respondents who own's only a car + No. of respondents who do not own any vehicle]
= 40 + 34 + 70
= 144
Percentage = 144/300 × 100 = 48%
Question 10 |
When a point inside of a tetrahedron (a solid with four triangular surfaces) is connected by straight lines to its corners, how many (new) internal planes are created with these lines? __________.
6 | |
7 | |
8 | |
9 |
→ If you take a point inside a tetrahedron, then you have 5 points.
→ An internal plane is formed by joining any of the three points.
→ No. of planes = 5 C 3 = 10
But 4 of them will be faces of tetrahedron.
∴ New planes = 10 - 4 = 6
Question 11 |
Consider the statement
“Not all that glitters is gold”
Predicate glitters(x) is true if x glitters and predicate gold(x) is true if x is gold. Which one of the following logical formulae represents the above statement?
∀x: glitters(x) ⇒ ¬gold(x) | |
∀x: gold(x) ⇒ glitters() | |
∃x: gold(x) ∧ ¬glitters(x) | |
∃x: glitters(x) ∧ ¬gold(x) |
Not all that glitters is gold.
Option A:
∀x:glitters(x) ⇒ ¬gold(x)
which means that every item (x), which glitters is not gold.
Option B:
∀x:gold(x) ⇒ glitters()
Every item (x) which is gold is a glitter.
(or)
Every golden item glitters.
Option C:
∃x: gold(x) ∧ ¬glitters(x)
There are some gold items which does not glitters.
Option D:
∃x:glitters(x) ∧ ¬gold(x)
There exists some glitters which are not gold.
(or)
Not all glitters are gold.
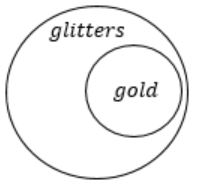
The answer is Option (D).
Method 2:
⇒ (∼∀x) (∼ (glitters(x) ⇒ gold(x))
⇒ ∃x (∼ (∼glitters(x) ∨ gold(x))
⇒ ∃x (glitters ∧ gold(x))
Question 12 |
Suppose you break a stick of unit length at a point chosen uniformly at random. Then the expected length of the shorter stick is ________.
0.25 | |
0.26 | |
0.27 | |
0.28 |
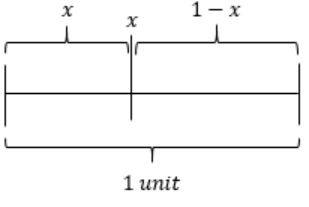
If we break at point x, length of the one piece x and the other piece is 1 – x.
Length of the shorter stick is between 0 to 0.5. If it is more than 0.5 then it will be longer stick.
The random variable (l) follows a uniform distribution. The probability function of l is
1/(b-a)=1/(0.5-0)=2 (length is between 0 to 0.5)
Expected value of length
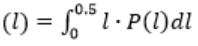
(where P(l) is the probability density function)
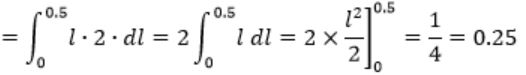
Question 13 |
Let G = (V,E) be a directed graph where V is the set of vertices and E the set of edges. Then which one of the following graphs has the same strongly connected components as G?
G1=(V,E1) where E1={(u,v)|(u,v)∉E} | |
G2=(V,E2 )where E2={(u,v)│(u,v)∈E} | |
G3=(V,E3) where E3={(u,v)|there is a path of length≤2 from u to v in E} | |
G4=(V4,E) where V4 is the set of vertices in G which are not isolated |
→ It strongly connected.
(A) G1=(V,E1) where E1={(u,v)|(u,v)∉E}
If (u, v) does not belong to the edge set ‘E’, then it indicates there are no edges. So, it is not connected.
(B) G2=(V,E2 )where E2={(u,v)│(u,v)∈E}
Given that ‘G’ is directed graph, i.e., it has path from each vertex to every other vertex.
Though direction is changed from (u, v) to (v, u), it is still connected component same as ‘G’.
(C) G3=(V,E3) where E3={(u,v)|there is a path of length≤2 from u to v in E}
This can also be true.
eg:
Both from each vertex to other vertex is also exists. So it is also strongly connected graph.
(D) G4=(V4,E) where V4 is the set of vertices in G which are not isolated.
If ‘G’ has same ‘x’ no. of isolated vertices, one strongly connected component
then no. of SCC = x + 1
G4 contain only ‘1’ component, which is not same as G.
Question 14 |
Consider the following system of equations:
- 3x + 2y = 1
4x + 7z = 1
x + y + z = 3
x – 2y + 7z = 0
The number of solutions for this system is _______.
1 | |
2 | |
3 | |
4 |
3x + 2y = 1
4x + 7z = 1
x + y + z = 3
x – 2y + 7z = 0
This is a non-homogeneous equation system.
The Augmented matrix for above set of equations is
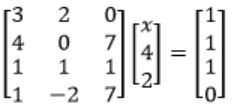
For matrix (A):
R4→ R4+R1
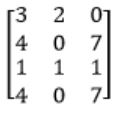
R4→ R4-R2
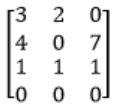
Rank = 3
For matrix (AB):
R4→(R4+R1 )-R2
Rank = 3
Rank of (A) = Rank (AB), so Unique solution
rank = 3 = no. of variables
Working Rule for Non-homogeneous equation:
(1) rank (A) < rank (AB), Inconsistent solution
(2) is rank (A) = rank (AB) = r then
if r = n, Unique solution
r < n, Infinite solution
Question 15 |
The value of the dot product of the eigenvectors corresponding to any pair of different eigenvalues of a 4-by-4 symmetric positive definite matrix is ________.
0 | |
1 | |
2 | |
3 |
The finite dimensional spectral theorem says that any symmetric matrix whose entries are real can be diagonalized by an orthogonal matrix.
Question 16 |
Let the function
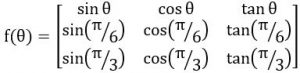
where 
and f(θ) denote the derivative of f with respect to θ. Which of the following is/are TRUE?
-
(I) There exists such that
such that f(θ)=0. (II) There exists such that
such that f(θ)≠0. I only | |
II only | |
Both I and II | |
Neither I nor II |
Rolle’s theorem states that for any continuous, differentiable function that has two equal values at two distinct points, the function must have a point on the function where the first derivative is zero. The technical way to state this is: if f is continuous and differentiable on a closed interval [a,b] and if f(a) = f(b), then f has a minimum of one value c in the open interval [a, b] so that f'(c) = 0.
We can observe that, sin, cos are continuous, but, Tan is not continuous at π/2. As the mentioned interval does not contain π/2, we can conclude that it is continuous.
As per Rolls theorem both statement 1 and statement 2 are true.