GATE 2014 [Set-3]
Question 1 |
While trying to collect(I) an envelope from under the table(II), Mr. X fell down (III) and was losing consciousness (IV) Which one of the above underlined parts of the sentence is NOT appropriate?
I | |
II | |
III | |
IV |
Question 2 |
If she _____________ how to calibrate the instrument, she ______________ done the experiment.
knows, will have | |
knew, had | |
had known, could have | |
should have known, would have |

Rule: If + past perfect then result to be perfect conditional (or) perfect continuous condition.
Then answer is Option C.
Question 3 |
Choose the word that is opposite in meaning to the word “coherent”.
sticky | |
well-connected | |
rambling | |
friendly |
Rambling = lengthy and confused (or) inconsequential
Question 4 |
Which number does not belong in the series below?
2, 5, 10, 17, 26, 37, 50, 64
17 | |
37 | |
64 | |
26 |
2 = 12+1
5 = 22+1
10 = 32+1
17 = 42+1
26 = 52+1
37 = 62+1
50 = 72+1
64 = 82+0
64 does not belong to the series.
Question 5 |
The table below has question-wise data on the performance of students in an examination. The marks for each question are also listed. There is no negative or partial marking in the examination.

What is the average of the marks obtained by the class in the examination?
1.34 | |
1.74 | |
3.02 | |
3.91 |
Total marks obtained = (21×2)+(15×3)+(23×2) = 133
Average marks = 133/44 = 3.02
Question 6 |
A dance programme is scheduled for 10.00 a.m. Some students are participating in the programme and they need to come an hour earlier than the start of the event. These students should be accompanied by a parent. Other students and parents should come in time for the programme. The instruction you think that is appropriate for this is
Students should come at 9.00 a.m. and parents should come at 10.00 a.m. | |
Participating students should come at 9.00 a.m. accompanied by a parent, and other parents and students should come by 10.00 a.m. | |
Students who are not participating should come by 10.00 a.m. and they should not bring their parents. Participating students should come at 9.00 a.m. | |
Participating students should come before 9.00 a.m. Parents who accompany them should come at 9.00 a.m. All others should come at 10.00 a.m. |
→ All other students and parents should come in time for the programme i.e. 10.00 am.
→ Option B is correct answer.
→ In option D, they gave, all other should come at 10.00 am that includes student's parents, staff and all others. So this is not correct option.
Question 7 |
By the beginning of the 20th century, several hypotheses were being proposed, suggesting a paradigm shift in our understanding of the universe. However, the clinching evidence was provided by experimental measurements of the position of a star which was directly behind our sun.
Which of the following inference(s) may be drawn from the above passage?
- (i) Our understanding of the universe changes based on the positions of stars
(ii) Paradigm shifts usually occur at the beginning of centuries
(iii) Stars are important objects in the universe
(iv) Experimental evidence was important in confirming this paradigm shift
(i), (ii) and (iv) | |
(iii) only | |
(i) and (iv) | |
(iv) only |
(i) is incorrect as it generalizes the experimental evidence of the star and assumes it to be always true, which may not be the case every time.
(ii) and (iii) is anyway wrong.
Hence, answer is option (D).
Question 8 |
The Gross Domestic Product (GDP) in Rupees grew at 7% during 2012-2013. For international comparison, the GDP is compared in US Dollars (USD) after conversion based on the market exchange rate. During the period 2012-2013 the exchange rate for the USD increased from Rs. 50/ USD to Rs. 60/ USD. India’s GDP in USD during the period 2012-2013
increased by 5% | |
decreased by 13% | |
decreased by 20% | |
decreased by 11% |
GDP in rupees = x
GDP in dollars = x/50
Increase in GDP in rupees = 7%
∴ New GDP in rupees = 1.07x
New GDP in dollars = 1.07x/60
Change = ((1.07x/60) - (x/50))/(x/50) = -6.5/60 = -10.83%
As it is negative, the value has decreased.
GDP in VSD has decreased by 11%.
Question 9 |
The ratio of male to female students in a college for five years is plotted in the following line graph. If the number of female students in 2011 and 2012 is equal, what is the ratio of male students in 2012 to male students in 2011?

1:1 | |
2:1 | |
1.5:1 | |
2.5:1 |
Male to female students ratio in 2011 = 1 : 1
Male to female students ratio in 2012 = 1.5 : 1 = 3 : 2
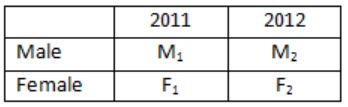
⇒ M1/F1 = 1:1
M1 = F1 ------- (1)
⇒ M2/F2 = 1:1
2M2 = 3F2 ------- (2)
Given,
F1 = F2 ------- (3) From (1) & (2)
M1/M2 = F1/(3F2/2) = 2F1/3F2
But from (3)
M1/M2 = 2/3
We need to find
M2 : M1 = 3 : 2 = 1.5 : 1
Question 10 |
Consider the equation: (7526)8 - (Y)8 = (4364)8, where (X)N stands for X to the base N. Find Y.
1634 | |
1737 | |
3142 | |
3162 |
⇒ 1/8 = (7526)8 - (4364)8
Base 8 ⇒ 0 to 7 digits
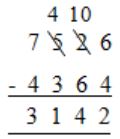
When you are borrowing you will add the value of the base, hence 2 becomes (2+8) = 10
Y = 3142
Question 11 |
Consider the following statements:
P: Good mobile phones are not cheap Q: Cheap mobile phones are not good L: P implies Q M: Q implies P N: P is equivalent to Q
Which one of the following about L, M, and N is CORRECT?
Only L is TRUE. | |
Only M is TRUE. | |
Only N is TRUE. | |
L, M and N are TRUE. |
So, given statement can be sub divided such that we can utilize the negation of this atomic statements.
Suppose, X is Good mobile and Y is cheap then
P: (Good(x) → ~cheap(x)) → (~good(x) ∨ ~cheap(x))
Q: cheap(x) → ¬good(x) ⟺ ((¬cheap(x) ∨ good(x)) ⟺ ¬good(x) ∨ ¬cheap(x))
All these are contra positive.
All L, M, N are true.
Question 12 |
Let X and Y be finite sets and f: X→Y be a function. Which one of the following statements is TRUE?
For any subsets A and B of X, |f(A ∪ B)| = |f(A)|+|f(B)| | |
For any subsets A and B of X, f(A ∩ B) = f(A) ∩ f(B) | |
For any subsets A and B of X, |f(A ∩ B)| = min{ |f(A)|,f|(B)|} | |
For any subsets S and T of Y, f -1 (S ∩ T) = f -1 (S) ∩ f -1 (T) |
We need to consider subsets of 'x', which are A & B (A, B can have common elements are exclusive).
Similarly S, T are subsets of 'y'.

To be a function, each element should be mapped with only one element.
(a) |f(A∪B)| = |f(A)|+|f(B)|
|{a,b,c}|∪|{c,d,e}| = |{a,b,c}| + |{c,d,e}|
|{a,b,c,d,e}| = 3+3
5 = 6 FALSE
(d) To get inverse, the function should be one-one & onto.
The above diagram fulfills it. So we can proceed with inverse.
f-1 (S∩T ) = f-1 (S)∩f-1 (T)
f-1 (c) = f-1 ({a,b,c})∩f-1 ({c,d,e})
2 = {1,2,3}∩{2,4,5}
2 = 2 TRUE
Question 13 |
Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L ≠ G and that the size of L is at least 4. The size of L is __________.
5 | |
6 | |
7 | |
8 |
So, 15 is divided by {1, 3, 5, 15}.
As minimum is 4 and total is 15, we eliminate 1,3,15.
Answer is 5.
Question 14 |
Which one of the following statements is TRUE about every n × n matrix with only real eigenvalues?
If the trace of the matrix is positive and the determinant of the matrix is negative, at least one of its eigenvalues is negative. | |
If the trace of the matrix is positive, all its eigenvalues are positive. | |
If the determinant of the matrix is positive, all its eigenvalues are positive. | |
If the product of the trace and determinant of the matrix is positive, all its eigenvalues are positive. |
• The product of the n eigenvalues of A is the same as the determinant of A. •
A: Yes, for sum to be negative there should be atleast one negative number.
B: There can be one small negative number and remaining positive, where sum is positive.
C: Product of two negative numbers is positive. So, there no need of all positive eigen values.
D: There is no need for all eigen values to be positive, as product of two negative numbers is positive.
Question 15 |
If V1 and V2 are 4-dimensional subspace of a 6-dimensional vector space V, then the smallest possible dimension of V1∩V2 is ______.
2 | |
3 | |
4 | |
5 |
For eg: a two dimensional vector space have x, y axis. For dimensional vector space, it have x, y, z axis.
In the same manner, 6 dimensional vector space has x, y, z, p, q, r (assume).
Any subspace of it, with 4 dimensional subspace consists any 4 of the above. Then their intersection will be atmost 2.
[{x,y,z,p} ∩ {r,q,p,z}] = #2
V1 ∩ V2 = V1 + V2 - V1 ∪ V2 = 4 + 4 + (-6) = 2
Question 16 |
If , then the value of k is equal to ________.
4 | |
5 | |
6 | |
7 |
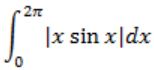
We have |xSinx|,

We can observe that it is positive from 0 to π and negative in π to 2π.
To get positive value from π to 2π we put ‘-‘ sign in the (π, 2π)

![GATE 2014 [Set-3]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)