HCU PHD CS MAY 2019
Question 1 |
Consider the polynomial p(x)=c0 + c1x + c2x^2 + c3x^3, where no coefficient is 0. The minimum number of multiplications required to evaluate p on an input x is
6 | |
4 | |
3 | |
8 |
Question 1 Explanation:
Given,
p(x)=c0 + c1x + c2x^2 + c3 x^3
For minimum number of multiplications, lets modify above equation,
p(x)= c0 + x(c1 + c2x + c3 x^2)
=c0+x(c1+x(c2+c3x)
=c0+x*(c1+x*(c2+c3*x)
Hence minimum number of multiplications required is 3
For minimum number of multiplications, lets modify above equation,
p(x)= c0 + x(c1 + c2x + c3 x^2)
=c0+x(c1+x(c2+c3x)
=c0+x*(c1+x*(c2+c3*x)
Hence minimum number of multiplications required is 3
Question 2 |
If S={x|0 < x < 12}, M={x|1 < x < 9} and N={x|0 < x< 5}, find M' ∩ N'
{x|9 ≤ x < 5} | |
{x|9 < x < 12}
| |
{x|0 < x < 12} | |
{x|5 < x < 9}
|
Question 2 Explanation:
S = Total range = {x| 0
Now,
M = {x| 1
M’ = {x| 0
and
N = {x| 0
N’ = {x| 5≤x<12}
Now, clearly the intersection range of M’ and N’ is,
{x| 9≤x<12}
M = {x| 1
N = {x| 0
Now, clearly the intersection range of M’ and N’ is,
{x| 9≤x<12}
Question 3 |
Let E, F and G be finite sets and let A = (E∩ F) - (F ∩ G) and B = (E - (E ∩ G)) - (E - F).
Which one of the following is true?
A ⊂ B | |
S ⊂ A | |
A = B | |
None of the above |
Question 3 Explanation:
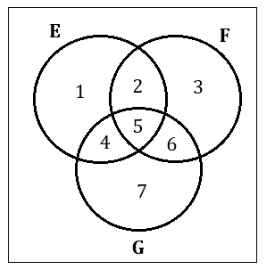
Now,
A = (E∩F) - (F∩G)
= (2,5) - (5,6)
= {2}
Also,
B = (E - (E∩G)) - (E - F)
= ({1,2,4,5} - {4,5}) - (1,4)
= (1,2) - (1,4)
= {2}
Hence A = B
Question 4 |
If the word FORGET is encoded as DPPHCU, then THINK is encoded as
VGKMM | |
RIILI | |
RIGOI | |
RIGOR |
Question 4 Explanation:

Question 5 |
Seven (distinct) road accidents occurred in a week. What is the probability that they all occurred
on the same day?
7^-6
| |
7^-2 | |
2^-7 | |
7^-7 |
Question 5 Explanation:
For every car accident we can choose a day in 7 ways. So total no. of ways in which 7 car accident can be assigned to 7 days = 7 × 7 × 7 × 7 × 7 × 7 × 7 = 77
Probability of accident happening on one day = 1/77
But there are 7 days in which we have to choose 1 day, in which all accidents are happening. Hence required probability is
7C1/77 = 7/77 = 1/76
Probability of accident happening on one day = 1/77
But there are 7 days in which we have to choose 1 day, in which all accidents are happening. Hence required probability is
7C1/77 = 7/77 = 1/76
Question 6 |
What is the maximum number of different Boolean functions involving n Boolean variables?
n^2^n | |
2^n | |
2^2^n | |
n^2 |
Question 6 Explanation:
No. of rows possible with n boolean variables is 2^n, and each row can have two functions possible . Hence the total number of boolean functions possible is 2^(2^n).
Question 7 |
Given below is a chart of rainfall amounts in Quinquinox city on a distant planet Quinox revolving around an equally distant Star. It has its own months and years. Year is, of course, the time takenin their own units of measurement to revolve once around their Star.
Examine the chart carefully and answer Question
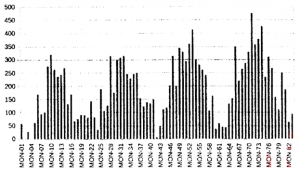
How many months are there in a year on Quinox?
10 | |
20 | |
28 | |
Not possible from the data given |
Question 8 |
Given below is a chart of rainfall amounts in Quinquinox city on a distant planet Quinox revolving around an equally distant Star. It has its own months and years. Year is, of course, the time taken in their own units of measurement to revolve once around their Star.
Examine the chart carefully and answer Question

If climate is classified into the following three categories,
QNd Seasonal rainfall with wet season being short
QNe Uniform rainfall throughout the year
QNm Seasonal rainfall with wet season being long
Which category describes the climate of Quinquinox?
QNm | |
QNe | |
QNd | |
Not possible from the data given |
Question 9 |

If the year on Quinox starts with Mon-Ol (which is also the first data point), which month in a year is the wettest?
18 | |
12 | |
8 | |
5 |
Question 10 |
Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S are
n^2 and n | |
n^2 and 0 | |
n(n+1)/2 and n | |
n(n+1)/2 and 0 |
Question 10 Explanation:
For the relation to be equivalence ,it should be
->Reflexive
->Symmetric
->Transitive
The smallest equivalence relation is on size n, which contains all diagonal elements.
The largest equivalence relation is the maximum size of relation itself ,i.e. n^2.
->Reflexive
->Symmetric
->Transitive
The smallest equivalence relation is on size n, which contains all diagonal elements.
The largest equivalence relation is the maximum size of relation itself ,i.e. n^2.
Question 11 |
Here is a puzzle: find a number x such that x leaves a remainder of 9 when divided by 10, a remainder of 8 when divided by 9, a remainder of 7 when divided by 8, ... , a remainder of 2 when divided by 3 and a remainder of 1 when divided by 2.
How many such numbers are there?
0 | |
Exactly 1 | |
2``` | |
Infinite |
Question 11 Explanation:
The lowest number divisible by all the numbers 1 to 10. So, for minimum value of N,
===-->N+1=2520 (LCM of 1,2,3,....10)
or,N=2519
This property is satisfied by the number N=2520∗K−1, where K is a positive integer.
===-->N+1=2520 (LCM of 1,2,3,....10)
or,N=2519
This property is satisfied by the number N=2520∗K−1, where K is a positive integer.
Question 12 |
Car A goes 200 Kms at an average speed of 40 Kmph in one direction and returns to the starting point covering the distance of 200 Kms at an average speed of 50 Kmph. Another Car B goes 200 Kms at an average speed of 45 Kmph and does the return journey of 200 Kms also at an average speed of 45 Kmph. Which statement is TRUE about the two cars A and B?
Car A takes less time than Car B | |
Car B takes less time than Car A | |
Both Cars A and B take the same time | |
Cannot be determined from the data given |
Question 12 Explanation:
Time taken by car A for complete journey = t1 + t2
= 200/40 + 200/50
= 5 + 4
= 9 hr
Time taken by car B for complete journey = t 1 + t2
= 200/45 + 200/45
= 8.88 hr
Car B takes less time than car A.
= 200/40 + 200/50
= 5 + 4
= 9 hr
Time taken by car B for complete journey = t 1 + t2
= 200/45 + 200/45
= 8.88 hr
Car B takes less time than car A.
Question 13 |
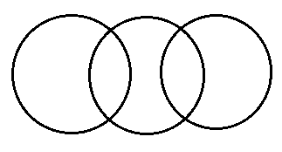
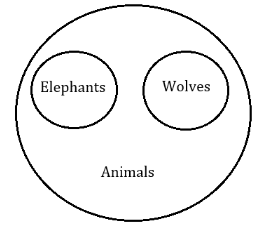
Which of the following is correctly represented by the Venn diagram above?
Elephants, Wolves, Animals | |
Dogs, Cats, Pets | |
Pigeons, Dogs, Birds | |
Tables, Chairs, Furniture |
Question 13 Explanation:
Let’s check option wise,
A) Can’t be the answer because all Elephants and Wolves are animals hence the diagram would be,

B) Yes, True. Because there are some dogs which are pets and there are some cats which are pets. Not all of them are pets. So in the given diagram naming will be,

C)Can’t be the answer because Dogs are not selected to be pigeons and birds.
D)Can’t be the answer because all Tables and chairs are furniture. Hence diagram will be same like (A).
A) Can’t be the answer because all Elephants and Wolves are animals hence the diagram would be,
B) Yes, True. Because there are some dogs which are pets and there are some cats which are pets. Not all of them are pets. So in the given diagram naming will be,
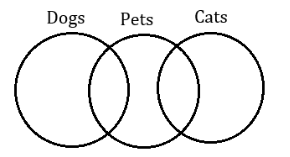
C)Can’t be the answer because Dogs are not selected to be pigeons and birds.
D)Can’t be the answer because all Tables and chairs are furniture. Hence diagram will be same like (A).
Question 14 |
Questions 14 - 16 are based on the Venn diagram below. S represents all integers between 1 and 30, P represents prime numbers between 1 and 30, M represents multiples of 3 between 1 and 30, and F represents all factors of 30.
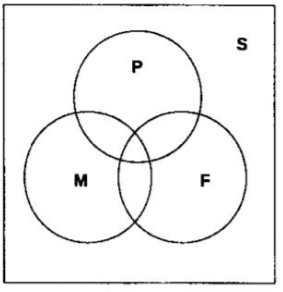
If G = P ∩ M ∩ F, then
G = {3}
| |
G = {3.5} | |
G = {1} | |
G={1,3,5} |
Question 14 Explanation:
S = 1, 2, 3, 4, …, 30
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
P∩M∩F = {3}
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
P∩M∩F = {3}
Question 15 |
Questions 14 - 16 are based on the Venn diagram below. S represents all integers between 1 and 30, P represents prime numbers between 1 and 30, M represents multiples of 3 between 1 and 30, and F represents all factors of 30.

What are the numbers in F but not in P or M?
1, 10 | |
Only 1 | |
Only 10 | |
1,3,10 |
Question 15 Explanation:
S = 1, 2, 3, 4, …, 30
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
F - (P∪M) = {1,2,3,5,6,10,15,30} - {2,3,5,6,7,9,11,12,13,15,17,18,19,21,23,24,27,29,30} = {1,10}
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
F - (P∪M) = {1,2,3,5,6,10,15,30} - {2,3,5,6,7,9,11,12,13,15,17,18,19,21,23,24,27,29,30} = {1,10}
Question 16 |
Questions 14 - 16 are based on the Venn diagram below. S represents all integers between 1 and 30, P represents prime numbers between 1 and 30, M represents multiples of 3 between 1 and 30, and F represents all factors of 30.

What is the cardinality of P ∩ F?
1 | |
2 | |
3 | |
4 |
Question 16 Explanation:
S = 1, 2, 3, 4, …, 30
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
P∩F = {2,3,5}
Hence cardinality of P∩F = 3
P = 2,3,5,7,11,13,17,19,23,29
M = 3,6,9,12,15,18,21,24,27,30
F = 1,2,3,5,6,10,15,30
P∩F = {2,3,5}
Hence cardinality of P∩F = 3
Question 17 |
Read the paragraphs below and answer Question.
When looking back on any kind of movement or revolution, one always likes to point to a beginning: "It began right there - it all started with so-and-so's famous speech ... " If structured
programming can be thought of as a revolution, then surely Dijkstra's land-mark paper, "Programming Considered as a Human Activity," published in 1965, marks its beginning. Virtually
the entire gospel of structured programming is contained in a few short pages: the arguments
against goto statements, the notion of top-down design, the emphasis on program correctness
and quality (or "elegance," as Dijkstra prefers to call it), and the strong argument against programs that modify themselves.
In addition to these fundamental concepts, there are some rather classic phrases that first appeared in this paper, and that have popped-up in dozens of subsequent articles and books. For
example, when discussing the "divide and conquer" approach characterizing top-down design,
Dijkstra admits, "I have only a very small head, ,and must live with it." What seems obvious to us today was a rather novel idea in 1965: the idea that while computers were - and still are
- getting faster and more powerful, human beings weren't.
This theme is repeated again and again, and is essentially the entire subject matter of Dijkstra's
1972 speech, "The Humble Programmer." ... Once you do read it, you can see why Dijkstra has
the reputation he does. His writing is succinct and yet convincing. Reading Dijkstra, someone
said, has been compared to eating marzipan - it's best to take very small bites, chew slowly,
and digest the mouthful before moving on to the next bite.
What is said to have begun with Dijkstra's landmark paper, "Programming Considered as a Human Activity" in 1965?
Structured programming | |
Programs which modify themselves that eventually led to viruses | |
High salaries to programmers
| |
Computer revolution |
Question 17 Explanation:
From the line
“ If structured programming can be thought of as a revolution, then surely Dijkstra's land-mark paper, "Programming Considered as a Human Activity," published in 1965, marks its beginning. ” , clearly the answer is (A) .
“ If structured programming can be thought of as a revolution, then surely Dijkstra's land-mark paper, "Programming Considered as a Human Activity," published in 1965, marks its beginning. ” , clearly the answer is (A) .
There are 17 questions to complete.
