Algorithms
Question 1 |

Which one of the following options arranges the functions in the increasing order of asymptotic growth rate?
A | f2, f3, f1 |
B | f3, f2, f1 |
C | f2, f1, f3 |
D | f1, f2, f3 |
The asymptotic notation order should be
Constant < logarithmic < linear < polynomial < exponential < factorial
F2 and F3 → Polynomial
F1 → Exponential
By the order of asymptotic notations F1 is definitely larger.
Method-1:
Consider n=100
F1 : 100 ^100 ⇒ 1.e+200
F2 : N^log(100) base 2 ⇒ 100 ^ log(100) base 2 ⇒ 100^6.6438561897747 = 1,93,96,00,91,15,564.181300016469223466
F3 : N^Sqrt(n) ====> 100^Sqrt(100) ⇒ 100^10 ⇒ 10,00,00,00,00,00,00,00,00,000
Method-2:
We can apply "log" on both sides.
log(F1)=nlog10 (base 2)
log(F2)=(logn)^2 = logn * logn (base 2)
log(F3)=sqrt(n)logn (base 2)
Answer: F2< F3< F1
Question 2 |
p[1] = 1, p[2] = 5, p[3] = 8, p[4] = 9, p[5] = 10, p[6] = 17, p[7] = 18
Which of the following statements is/are correct about R7?
A | R7is achieved by three different solutions.
|
B | R7=18 |
C | R7=19 |
D | R7cannot be achieved by a solution consisting of three pieces. |

There are 3 different possible ways to get the maximum amount.
P[6] + P[1] → 17+1 = 18
P[2] + P[2] + P[3] → 5+5+8 = 18
P[7] → 18 = 18
Question 3 |
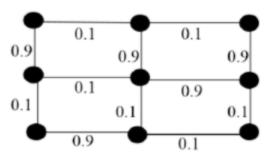
The number of minimum-weight spanning trees of the graph is _______
A | 3 |
To find the number of spanning trees using 2 methods:
- If graph is complete, use n^n-2 formula
- If graph is not complete, then use kirchhoff theorem.
Steps in Kirchoff’s Approach:
(i) Make an Adjacency matrix.
(ii) Replace all non-diagonal is by – 1.
(iii) Replace all diagonal zero’s by the degree of the corresponding vertex.
(iv) Co-factors of any element will give the number of spanning trees.
Using the Kirchhoff theorem will take lot of time because the number of vertices are 9.
So, we use brute force technique to solve the problem with the help of Kruskal's algorithm.


Question 4 |
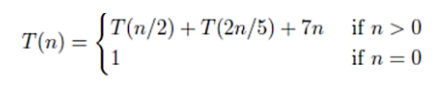
Which one of the following options is correct?
A |  |
B | 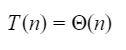 |
C |  |
D | 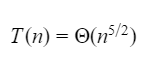 |

Question 5 |

Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?
A | Quicksort using the last element as pivot |
B | Insertion sort |
C | Selection sort |
D | Mergesort |
Quick sort(with last element as pivot) → will give the worst case time complexity as O(n^2).
Merge Sort → The merge sort will not depend upon the input order and will give O(nlogn) time complexity.
Insertion Sort → Insertion sort will perform best case time complexity when the input array is in sorted order. If the array is already sorted then the inversion count is 0 and If the array is sorted in reverse order that inversion count is the maximum.
Note: Inversion formal definition is two elements A[i] and A[j] form an inversion if A[i] > A[j] and i < j.
The number of comparisons will not take more than “n” for the given input array.
Selection Sort → Selection sort will not depend upon the input order and will give O(n^2) time complexity.
Question 6 |
A | 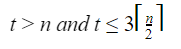 |
B | 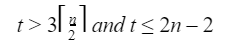 |
C |  |
D |  |
Let assume n=512
Method-1:
Using standard recursive algorithm:

MaxMin is a recursive algorithm that finds the maximum and minimum of the set of elements {a(i), a(i+1), ..., a(j)}. The situation of set sizes one (i=j) and two (i=j-1) are handled separately. For sets containing more than two elements, the midpoint is determined ( just as in binary search) and two new subproblems are generated. When the maxima and minima of these subproblems are determined, the two maxima are compared and the two minima are compared to achieve the solution for the entire set.
To find the number of element comparisons needed for Maxmin, T(n) represents this number, then the resulting recurrence relation is
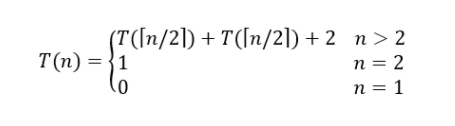
When n is a power of two, n = 2k for some positive integer k, then
T(n)=2T(n/2)+2
=2(2T(n/4)+2)+2
=4T(n/4)+4+2
፧
=2k-1T(2)+1ik-12i
=2k-1+2k-2
=3n/2-2
→ The given example n=512
Apply into 3n/2 -2
= (3*512)/2 -2
= 768-2
= 766
Method-2:
Find the minimum and maximum independently, using n-1 comparisons for each, for a total of 2n-2 comparisons. In fact, at most 3⌊n/2⌋ comparisons are sufficient to find both the minimum and the maximum. The strategy is to maintain the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, at a cost of 2 comparisons per element, we process elements in pairs. We compare pairs of elements from the input first with each other, and then we compare the smaller to the current minimum and the larger to the current maximum, at a cost of 3 comparisons for every 2 elements.
Setting up initial values for the current minimum and maximum depends on whether n is odd or even. If n is odd, we set both the minimum and maximum to the value of the first element,and then we process the rest of the elements in pairs. If n is even, we perform 1 comparison on the first 2 elements to determine the initial values of the minimum and maximum, and then process the rest of the elements in pairs as in the case for odd n.
Let us analyze the total number of comparisons. If n is odd, then we perform 3⌊n/2⌋ comparisons. If n is even, we perform 1 initial comparison followed by 3(n-2)/2 comparisons, for a total of (3n/2)-2. Thus, in either case, the total number of comparisons is at most 3⌊n/2⌋.
Given an even number of elements. So, 3n/2 -2 comparisons.
= (3*512)/2 -2
= 768-2
= 766
Method-3:
By using Tournament Method:
Step-1: To find the minimum element in the array will take n-1 comparisons.
We are given 512 elements. So, to find the minimum element in the array will take 512-1= 511
Step-2: To find the largest element in the array using the tournament method.
- After the first round of Tournament , there will be exactly n/2 numbers =256 that will lose the round.
- The biggest loser (the largest number) should be among these 256 loosers.To find the largest number will take (n/2)−1 comparisons =256-1 = 255
Total 511+255= 766
Question 7 |
The root directory of a disk should be placed
A | at a fixed address in main memory |
B | at a fixed location on the disk |
C | anywhere on the disk |
D | at a fixed location on the system disk |
E | anywhere on the system disk |
Question 8 |
Consider a simple connected graph G with n vertices and n-edges (n>2). Then, which of the following statements are true?
A | G has no cycles. |
B | The graph obtained by removing any edge from G is not connected. |
C | G has at least one cycle. |
D | The graph obtained by removing any two edges from G is not connected. |
E | Both C and D. |
For example let us consider, n=3.
Question 9 |
![]() where O(n) stands for order n is:
where O(n) stands for order n is:
A | O(n) |
B | O(n2) |
C | O(n3) |
D | O(3n2) |
E | O(1.5n2) |
F | B, C, D and E |
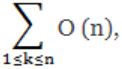
⇒ In this 'n' is constant. So, n is added to n times itself which is O(n2).
Hence, (a) is wrong. And rest (B), (C), (D), (E) are correct.
Question 10 |
Consider the recursive algorithm given below:
procedure bubblersort (n);
var i,j: index; temp : item;
begin
for i:=1 to n-1 do
if A[i] > A [i+1] then
begin
temp : A[i];
A[i]:=A[i+1];
A[i+1]:=temp
end;
bubblesort (n-1)
end
Let an be the number of times the ‘if…then….’ Statement gets executed when the algorithm is run with value n. Set up the recurrence relation by defining an in terms of an-1. Solve for an.
A | Theory Explanation. |
Question 11 |
FORTRAN implementation do not permit recursion because
A | they use static allocation for variables |
B | they use dynamic allocation for variables |
C | stacks are not available on all machines |
D | it is not possible to implement recursion on all machines |
→ Recursion requires dynamic allocation of data.
Question 12 |
The recurrence relation that arises in relation with the complexity of binary search is:
A | T(n) = T(n/2) + k, k a constant |
B | T(n) = 2T(n/2) + k, k a constant |
C | T(n) = T(n/2) + log n |
D | T(n) = T(n/2) + n |
∴ T(n) = 2T(n/2) + k, k a constant
Question 13 |
Which of the following algorithm design techniques is used in the quicksort algorithm?
A | Dynamic programming |
B | Backtracking |
C | Divide and conquer |
D | Greedy method |
Question 14 |
In which one of the following cases is it possible to obtain different results for call-by reference and call-by-name parameter passing methods?
A | Passing a constant value as a parameter |
B | Passing the address of an array as a parameter |
C | Passing an array element as a parameter |
D | Passing an array following statements is true |
{ ........
a[ ] = {1, 2, 3, 4}
i = 0
fun(a[i]);
print a[0];
}
fun(int x)
{
int i = 1;
x = 8;
}
O/p:
Call-by-reference = 8
Call-by-value = 1
Question 15 |
Which one of the following statements is false?
A | Optimal binary search tree construction can be performed efficiently using dynamic programming. |
B | Breadth-first search cannot be used to find connected components of a graph. |
C | Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed. |
D | Depth-first search can be used to find connected components of a graph. |
Question 16 |
Consider the following two functions:
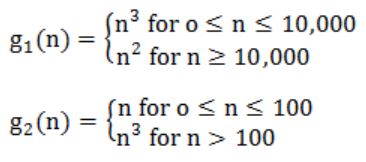
Which of the following is true?
A | g1(n) is O(g2(n)) |
B | g1 (n) is O(3) |
C | g2 (n) is O(g1 (n)) |
D | g2 (n) is O(n) |
E | Both A and B |
Growth rate of g1 is less than that of g2 i.e., g1(n) = O(g2(n)) = O(n).
Question 17 |
An array A contains n integers in locations A[0],A[1], …………… A[n-1]. It is required to shift the elements of the array cyclically to the left by K places, where 1≤K≤n-1. An incomplete algorithm for doing this in linear time, without using another is given below. Complete the algorithm by filling in the blanks. Assume all variables are suitably declared.
min:=n;
i=0;
while _____do
begin
temp:=A[i];
j:=i;
while _____do
begin
A[j]:=_____;
j:=(j+K) mod n;
if jA | Theory Explanation. |
Question 18 |
(a) Use the patterns given to prove that
(You are not permitted to employ induction)

(b) Use the result obtained in (a) to prove that
A | Theory Explanation. |
Question 19 |
Consider the following recursive function:
function fib (1:integer);integer; begin if (n=0) or (n=1) then fib:=1 else fib:=fib(n-1) + fib(n-2) end;
The above function is run on a computer with a stack of 64 bytes. Assuming that only return address and parameter and passed on the stack, and that an integer value and an address takes 2 bytes each, estimate the maximum value of n for which the stack will not overflow. Give reasons for your answer.
A | Theory Explanation. |
Question 20 |
An independent set in a graph is a subset of vertices such that no two vertices in the subset are connected by an edge. An incomplete scheme for a greedy algorithm to find a maximum independent set in a tree is given below:
V: Set of all vertices in the tree; I:=φ;
While V ≠ φdo
begin
select a vertex u; ∈ V such that
V:= V – {u};
if u is such that
then 1:= I ∪ {u}
end;
output(I);
(a) Complete the algorithm by specifying the property of vertex u in each case
(b) What is the time complexity of the algorithm.
A | Theory Explanation. |
Question 21 |
Merge sort uses
A | Divide and conquer strategy |
B | Backtracking approach |
C | Heuristic search |
D | Greedy approach |
Question 22 |
The postfix expression for the infix expression
A + B*(C + D)/F + D*E is:
A | AB + CD + *F/D + E* |
B | ABCD + *F/DE*++ |
C | A *B + CD/F *DE++ |
D | A + *BCD/F* DE++ |
E | None of the above |
A B C D + * F / + D E * +
Question 23 |
Which of the following statements is true?
- I. As the number of entries in a hash table increases, the number of collisions increases.
II. Recursive programs are efficient
III. The worst case complexity for Quicksort is O(n2)
A | I and II |
B | II and III |
C | I and IV |
D | I and III |
Recursive program requires stack for storing the function state. Any recursive program can be rewritten as an iterative one. Advantage of recursion is "less programming effort", while it always lags behind iterative one in terms of performance.
Question 24 |
Consider the following sequence of numbers
92, 37, 52, 12, 11, 25
Use bubble sort to arrange the sequence in ascending order. Give the sequence at the end of each of the first five passes.
A | Theory Explanation. |
Question 25 |
How many minimum spanning trees does the following graph have? Draw them. (Weights are assigned to the edge).

A | Theory Explanation. |
Question 26 |
For parameters a and b, both of which are ω(1), T(n) = T(n1/a)+1, and T(b)=1.
Then T(n) is
A | θ(loga logb n) |
B | θ(logb loga n)
|
C | θ(log2 log2 n)
|
D | θ(logab n)
|
T(n) = [T(n1/a2)+1] + 1
= [T(n1/a3)+1] + 2
= [T(n1/a3)] + 3
= [T(n1/ak)] + b
= logb n = ak
= log logb n = k log a
= k= loga logb n
T(n)=1+loga logb n
T(n)=O(loga logb n)
Question 27 |
Let G = (V,E) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighted edge (u,v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
A | θ(|E|+|V|) |
B | θ(|E| log|V|) |
C | θ(|E||V|) |
D | θ(|V|) |
• As T is a minimum spanning tree and we need to add a new edge to existing spanning tree.
• Later we need to check still T is a minimum spanning tree or not, So we need to check all vertices whether there is any cycle present after adding a new edge.
• All vertices need to traverse to confirm minimum spanning tree after adding new edge then time complexity is O(V).
Method-2:
Time Complexity:
Total vertices: V, Total Edges : E
• O(logV) – to extract each vertex from the queue. So for V vertices – O(VlogV)
• O(logV) – each time a new pair object with a new key value of a vertex and will be done at most once for each edge. So for total E edge – O(ElogV)
• So overall complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)
Note: Method-1 is the most appropriate answer for giving a question.
Question 28 |
Consider a graph G = (V, E), where V = {v1, v2, …, v100}, E = {(vi, vj) | 1 ≤ i < j ≤ 100}, and weight of the edge (vi, vj) is |i - j|. The weight of the minimum spanning tree of G is ______.
A | 99 |
• N =100
• Edge weight is |i-j| for Edge (vi,vj) {1<=i<=100}
• The weight of edge(v1,v2) is 1 , edge(v5,v6) is 1.
• So, 99 edges of weight is 99.
Question 29 |
Which of the following is false?
A |  |
B | 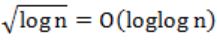 |
C | 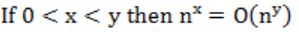 |
D |  |

Question 30 |
The recurrence relation
T(1) = 2 T(n) = 3T(n/4)+n
has the solution, T(n) equals to
A | O(n) |
B | O(log n) |
C | O(n3/4) |
D | None of the above |
Question 31 |
The average number of key comparisons done on a successful sequential search in list of length n is
A | log n |
B | n-1/2 |
C | n/2 |
D | n+1/2 |
= No. of comparisons if element present in 1st position + No. of comparisons if element present in 2nd position + ............. + No. of comparisons if element present in nth position
= 1 + 2 + 3 + ... + n
= n(n+1)/2
Since there are n elements in the list, so average no. of comparisons
= Total comparisons/Total no. of elements
= (n(n+1)/2)/n
= n+1/2
Question 32 |
Quicksort is run on two inputs shown below to sort in ascending order taking first element as pivot,
(i) 1,2,3,...,n (ii) n,n-1,n-2,...,2,1
Let C1 and C2 be the number of comparisons made for the inputs (i) and (ii) respectively. Then,
A | C1 < C2 |
B | C1 > C2 |
C | C1 = C2 |
D | we cannot say anything for arbitrary n. |
So, option is (C) is correct.
Question 33 |
A two dimensional array A[1...n][1...n] of integers is partially sorted if
∀i, j ∈ [1...n−1], A[i][j] < A[i][j+1] and
A[i][j] < A[i+1][j]
Fill in the blanks:
(a) The smallest item in the array is at A[i][j] where i=............and j=..............
(b) The smallest item is deleted. Complete the following O(n) procedure to insert item x (which is guaranteed to be smaller than any item in the last row or column) still keeping A partially sorted.
procedure insert (x: integer);
var i,j: integer;
begin
(1) i:=1; j:=1, A[i][j]:=x;
(2) while (x > ...... or x > ......) do
(3) if A[i+1][j] < A[i][j] ......... then begin
(4) A[i][j]:=A[i+1][j]; i:=i+1;
(5) end
(6) else begin
(7) ............
(8) end
(9) A[i][j]:= .............
end
A | Theory Explanation. |
Question 34 |
Insert the characters of the string K R P C S N Y T J M into a hash table of size 10.
Use the hash function
h(x) = (ord(x) – ord("a") + 1) mod10
and linear probing to resolve collisions.
(a) Which insertions cause collisions?
(b) Display the final hash table.
A | Theory Explanation. |
Question 35 |
A complete, undirected, weighted graph G is given on the vertex {0, 1,...., n−1} for any fixed ‘n’. Draw the minimum spanning tree of G if
(a) the weight of the edge (u,v) is ∣u − v∣
(b) the weight of the edge (u,v) is u + v
A | Theory Explanation. |
Question 36 |
Let G be the directed, weighted graph shown in below figure.
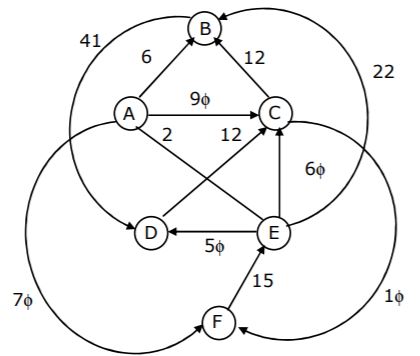
We are interested in the shortest paths from A.
(a) Output the sequence of vertices identified by the Dijkstra’s algorithm for single source shortest path when the algorithm is started at node A.
(b) Write down sequence of vertices in the shortest path from A to E.
(c) What is the cost of the shortest path from A to E?
A | Theory Explanation. |
Question 37 |
Consider the following program that attempts to locate an element x in a sorted array a[] using binary search. Assume N>1. The program is erroneous. Under what conditions does the program fail?
var i,j,k: integer; x: integer;
a:= array; [1...N] of integer;
begin i:= 1; j:= N;
repeat k:(i+j) div 2;
if a[k] < x then i:= k
else j:= k
until (a[k] = x) or (i >= j);
if (a[k] = x) then
writeln ('x is in the array')
else
writeln ('x is not in the array')
end; A | Theory Explanation. |
Question 38 |
Consider a sequence of 14 elements: A = [-5, -10, 6, 3, -1, -2, 13, 4, -9, -1, 4, 12, -3, 0]. The subsequence sum ![]() . Determine the maximum of S(i,j), where 0 ≤ i ≤ j < 14. (Divide and conquer approach may be used)
. Determine the maximum of S(i,j), where 0 ≤ i ≤ j < 14. (Divide and conquer approach may be used)
A | 19 |
B | 39 |
C | 29 |
D | 09 |
Ex:
{A, B, C, D}
{A, AB, AC, AD, ABC, ABD, ACD, B, BC, BD, BCD, C, CD, D }
Step-1: Array of elements A = [-5, -10, 6, 3, -1, -2, 13, 4, -9, -1, 4, 12, -3, 0 ]
Step-2: As per the given question, if they want to find maximum subsequence means
{6,3,13,4,4,12}
= 42
Step-3: But according to given recurrence relation, the sequence should be continuous. {6,3,13,4,4,12}.
This is not continuous subsequence.
Step-4: The continuous sequence is {6, 3, -1, -2, 13, 4, -9, -1, 4, 12}
Total is {29}.
Note: We can't get more than 29 maximum subsequence sum.
Question 39 |
An array of 25 distinct elements is to be sorted using quicksort. Assume that the pivot element is chosen uniformly at random. The probability that the pivot element gets placed in the worst possible location in the first round of partitioning (rounded off to 2 decimal places) is _____.
A | 0.08 |
B | 0.01 |
C | 1 |
D | 8 |
Step-2: Pivot element = uniformly random.
Step-3: Worst case position in the pivot element is either first (or) last.
Step-4: So total 2 possibilities among 25 distinct elements
= 2/25
= 0.08
Question 40 |
There are n unsorted arrays: A1, A2, ..., An. Assume that n is odd. Each of A1, A2, ..., An contains n distinct elements. There are no common elements between any two arrays. The worst-case time complexity of computing the median of the medians of A1, A2, ..., An is
A | O(n) |
B | O(n log n) |
C | Ω(n2 log n) |
D | O(n2) |
But it is similar to quicksort but in quicksort, partitioning will take extra time.
→ Find the median will be (i+j)/2
1. If n is odd, the value is Ceil((i+j)/2)
2. If n is even, the value is floor((i+j)/2)
-> Here, total number of arrays are
⇒ O(n)*O(n)
⇒ O(n2)
Note:
They are clearly saying that all are distinct elements.
There is no common elements between any two arrays.
Question 41 |
I. G has a unique minimum spanning tree, if no two edges of G have the same weight.
II. G has a unique minimum spanning tree, if, for every cut of G, there is a unique minimum-weight edge crossing the cut.
Which of the above statements is/are TRUE?
A | I only |
B | II only |
C | Both I and II |
D | Neither I nor II |
I. TRUE: G Graph is unique, no two edges of the graph is same.

Step-1: Using Kruskal's algorithm, arrange each weights in ascending order.
17, 18, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
Step-2:

Step-3: 17 + 18 + 20 + 21 + 22 + 23 + 26 = 147
Step-4: Here, all the elements are distinct. So, the possible MCST is 1.
II. TRUE: As per the above graph, if we are cut the edge, that should the be the minimum edge.
Because we are already given, all minimum edge weights if graph is distinct.
Question 42 |
The correct matching for the following pairs is
(A) All pairs shortest path (1) Greedy (B) Quick Sort (2) Depth-First search (C) Minimum weight spanning tree (3) Dynamic Programming (D) Connected Components (4) Divide and and Conquer
A | A – 2 B – 4 C – 1 D – 3 |
B | A – 3 B – 4 C – 1 D – 2 |
C | A – 3 B – 4 C – 2 D – 1 |
D | A – 4 B – 1 C – 2 D – 3 |
Quick sort - Divide and Conquer
Minimum weight Spanning tree - Greedy
Connected components - Depth-First search
Question 43 |
Let T(n) be the function defined by T(1)= 1, T(n)= 2T(⌊n/2⌋) + √n for n≥2. Which of the following statement(s) is true?
A | T(n) = O(√n) |
B | T(n) = O(n) |
C | T(n) = O(log n) |
D | None of the above |
Question 44 |
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?
A | Dynamic programming |
B | Backtracking |
C | Greedy |
D | Divide and Conquer |
Question 45 |
Give the correct matching for the following pairs:
A. O(log n) 1. Selection sort
B. O(n) 2. Insertion sort
C. O(nlog n) 3. Binary search
D. O(n2) 4. Merge sort A | A – R B – P C – Q D – S |
B | A – R B – P C – S D – Q |
C | A – P B – R C – S D – Q |
D | A – P B – S C – R D – Q |
Selection = O(n)
Merge sort = O(n log n)
Insertion sort = O(n2)
Question 46 |
(a) Solve the following recurrence relation:
xn = 2xn-1 - 1, n>1 x1 = 2
(b) Consider the grammar
S → Aa | b A → Ac | Sd | ε
Construct an equivalent grammar with no left recursion and with minimum number of production rules.
A | Theory Explanation. |
Question 47 |
A sorting technique is called stable if
A | it takes O (nlog n) time |
B | it maintains the relative order of occurrence of non-distinct elements |
C | it uses divide and conquer paradigm |
D | it takes O(n) space |
Question 48 |
Suppose we want to arrange the n numbers stored in any array such that all negative values occur before all positive ones. Minimum number of exchanges required in the worst case is
A | n - 1 |
B | n |
C | n + 1 |
D | None of the above |
Now we will swap 1st no. with nth no. and then 2nd no. with (n-1)th no. and then 3rd no. with (n-2)th and so on. Like this we will have to do n/2 swaps in worst case.
Question 49 |
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
then the order of these elements after second pass of the algorithm is:
A | 8, 9, 15, 20, 47, 4, 12, 17, 30, 40 |
B | 8, 15, 20, 47, 4, 9, 30, 40, 12, 17 |
C | 15, 20, 47, 4, 8, 9, 12, 30, 40, 17 |
D | 4, 8, 9, 15, 20, 47, 12, 17, 30, 40 |

Question 50 |
If n is a power of 2, then the minimum number of multiplications needed to compute a* is
A | log2 n |
B | √n |
C | n-1 |
D | n |
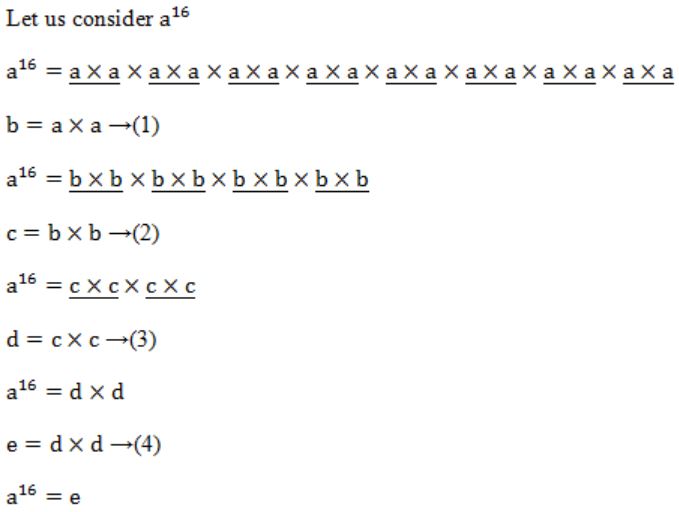
We require 4 multiplications to calculate a16 .....(I)
→ Like that 3 multiplications requires to calculate a8 .....(II)
I, II are satisfied with the option A.
