TIFR PHD CS & SS 2012
Question 1 |
Amar and Akbar both tell the truth with probability 3/4 and lie with probability 1/4. Amar watches a test match and talks to Akbar about the outcome. Akbar, in turn, tells Anthony, “Amar told me that India won”.
What probability should Anthony assign to India’s win?
What probability should Anthony assign to India’s win?
9/16 | |
6/16 | |
7/16 | |
10/16 | |
None of the above |
Question 2 |
If Mr.M is guilty, then no witness is lying unless he is afraid. There is a witness who is afraid. Which of the following statements is true?
(Hint: Formulate the problem using the following predicates
G – Mr. M is guilty
W(x) – x is a witness
L(x) – x is lying
A(x) – x is afraid )
(Hint: Formulate the problem using the following predicates
G – Mr. M is guilty
W(x) – x is a witness
L(x) – x is lying
A(x) – x is afraid )
Mr.M is guilty | |
Mr.M is not guilty | |
From these facts one cannot conclude that Mr.M is guilty | |
There is a witness who is lying | |
No witness is lying. |
Question 3 |
Long ago, in a planet far far away, there lived three races of intelligent inhabitants: the Blues (who always tell the truth), the Whites (who always lie), and the Pinks (who, when asked a series of questions, start with a lie and then tell the truth and lie alternately). To three creatures, chosen from the planet and seated facing each other at A, B and C (see figure), the following three questions are put:
(i) What race is your left-hand neighbour?
(ii) What race is your right-hand neighbour?
(iii) What race are you?

Here are their answers:
A: (i) White (ii) Pink (iii) Blue
B: (i) Pink (ii) Pink (iii) Blue
C: (i) White (ii) Blue (iii) Blue
What is the actual race of each of the three creatures?
(i) What race is your left-hand neighbour?
(ii) What race is your right-hand neighbour?
(iii) What race are you?
Here are their answers:
A: (i) White (ii) Pink (iii) Blue
B: (i) Pink (ii) Pink (iii) Blue
C: (i) White (ii) Blue (iii) Blue
What is the actual race of each of the three creatures?
A is Pink, B is White, C is Blue | |
A is Blue, B is Pink, C is White | |
A is Pink, B is Blue, C is Pink | |
A is White, B is pink, C is blue | |
Cannot be determined from the above data |
Question 4 |
Let ABC be a triangle with n distinct points inside. A triangulation of ABC with respect to the n points is obtained by connecting as many points as possible such that no more line segment can be added without intersecting other line segments. In other words, ABC has been partitioned into triangles with end points at the n points or at the vertices A, B, C. For example, the following figure gives one possible triangulation of ABC with two points inside it.

Although there are many different ways to triangulate ABC with the n points inside, the number of triangles depends only on n. In the above figure it is five. How many triangles are there in a triangulation of ABC with n points inside it?
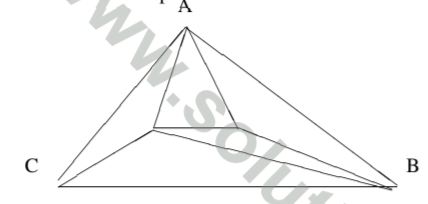
Although there are many different ways to triangulate ABC with the n points inside, the number of triangles depends only on n. In the above figure it is five. How many triangles are there in a triangulation of ABC with n points inside it?
3n − 1 | |
n2 + 1 | |
n + 3
| |
2n + 1 | |
4n − 3 |
Question 5 |
What is the maximum number of points of intersection between the diagonals of a convex octagon (8-vertex planar polygon)? Note that a polygon is said to be convex if the line segment joining any two points in its interior lies wholly in the interior of the polygon. Only points of intersection between diagonals that lie in the interior of the octagon are to be considered for this problem.
55 | |
60 | |
65 | |
70 | |
75 |
Question 6 |
A certain pair of used shoes can be repaired for Rs. 1250 and will last for 1 year. A pair of the same kind of shoes can be purchased new for Rs. 2800 and will last for 2 years. The average cost per year of the new shoes is what percent greater than the cost of repairing the used shoes?
5% | |
12% | |
15% | |
3% | |
24% |
Question 7 |
It is required to divide the 2n members of a club into n disjoint teams of 2 members each. The teams are not labelled. The number of ways in which this can be done is:
a | |
b | |
c | |
d | |
e |
Question 8 |
How many pairs of sets (A, B) are there that satisfy the condition A, B ⊆ {1, 2, . . . , 5}, A ∩ B = {}?
125 | |
127 | |
130 | |
243 | |
257 |
Question 9 |
The probability of throwing six perfect dices and getting six different faces is
1 − 6!/66 | |
6!/66 | |
6-6 | |
1-6-6 | |
None of the above |
Question 10 |
In how many different ways can r elements be picked from a set of n elements if
(i) Repetition is not allowed and the order of picking matters?
(ii) Repetition is allowed and the order of picking does not matter?

(i) Repetition is not allowed and the order of picking matters?
(ii) Repetition is allowed and the order of picking does not matter?
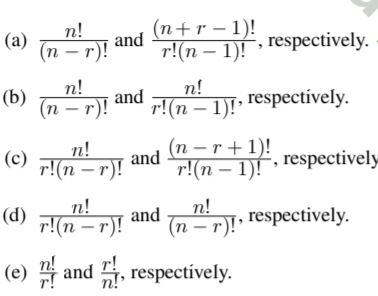
a | |
b | |
c | |
d | |
e |
Question 11 |
Let N be the sum of all numbers from 1 to 1023 except the five primes numbers: 2, 3, 11, 17, 31. Suppose all numbers are represented using two bytes (sixteen bits). What is the value of the least significant byte (the least significant eight bits) of N?
00000000 | |
10101110 | |
01000000 | |
10000000 | |
11000000 |
Question 12 |
For the polynomial p(x) = 8x10 − 7x3 + x − 1 consider the following statements (which may be true or false)
(i) It has a root between [0, 1].
(ii) It has a root between [0, −1].
(iii) It has no roots outside (−1, 1).
Which of the above statements are true?
(i) It has a root between [0, 1].
(ii) It has a root between [0, −1].
(iii) It has no roots outside (−1, 1).
Which of the above statements are true?
Only (i) | |
Only (i) and (ii) | |
Only (i) and (iii) | |
Only (ii) and (iii) | |
All of (i), (ii) and (iii) |
Question 13 |
The maximum value of the function
f(x, y, z) = (x − 1/3)2 + (y − 1/3)2 + (z − 1/3)2
subject to the constraints
x + y + z = 1, x ≥ 0, y ≥ 0, z ≥ 0
f(x, y, z) = (x − 1/3)2 + (y − 1/3)2 + (z − 1/3)2
subject to the constraints
x + y + z = 1, x ≥ 0, y ≥ 0, z ≥ 0
1/3 | |
2/3 | |
1 | |
4/3 | |
4/9 |
Question 14 |
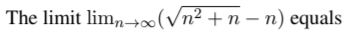
∞ | |
1 | |
1/2 | |
0 | |
None of the above |
Question 15 |
Consider the differential equation dx/dt = (1−x)(2−x)(3−x). Which of its equilibria is unstable?
x = 0 | |
x = 1 | |
x = 2 | |
x = 3 | |
None of the above |
There are 15 questions to complete.
