TIFR PHD CS & SS 2016

Question 1
Suppose the following statements about three persons in a room are true.
"Chandni, Sooraj and Tara are in a room. nobody else is in the room.
Chandni is looking at Sooraj. Sooraj is looking at Tara.
Chandni is married. Tara is not married.
A married person in the room is looking at an unmarried person."
Then, which of the following is necessarily true?
A
Sooraj is married
B
Sooraj is unmarried
C
The situation described is impossible
D
There is insufficient information to conclude if Sooraj is married or unmarried
E
None of the above
Mathematical-ReasoningLogical-Reasoning
Question 2
A
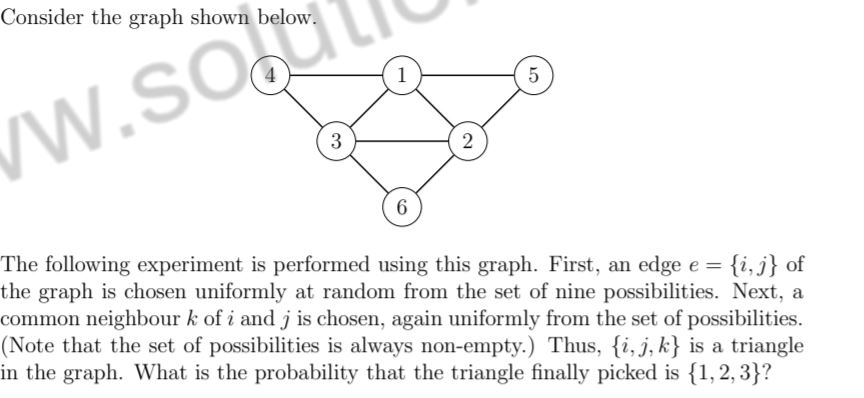
1/6
B
1/4
C
1/3
D
2/3
E
5/6
Engineering-MathematicsProbability-and-statistics
Question 3
A
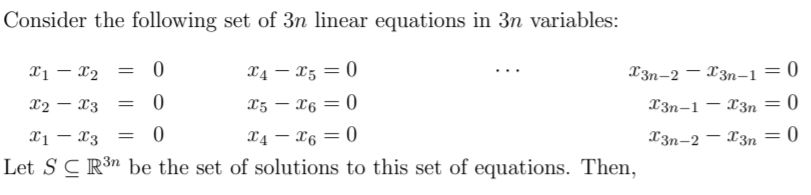
S is empty
B
S is a subspace of R3n of dimension 1
C
S is a subspace of R3n of dimension n
D
S is a subspace of R3n of dimension n − 1
E
S has exactly n elements
Engineering-MathematicsLinear-Equation
Question 4
A
(n-1)/2
B
0
C
1
D
n/4
E
(n 2)
Engineering-MathematicsProbability-and-statistics
Question 5
A
a
B
b
C
c
D
d
E
e
Engineering-MathematicsCalculus
Question 6
Which of the following statements about the eigen values of In, the nXn identity matrix (over complex numbers), is true?
A
The eigen values are 1, ω, ω2, . . . , ωn−1, where ω is a primitive n-th root of unity
B
The only eigen value is −1
C
Both 0 and 1 are eigen values, but there are no other eigen values
D
The eigen values are 1, 1/2, 1/3, . . . , 1/n
E
The only eigen value is 1
Engineering-MathematicsLinear-Algebra
Question 7
Let S be the 4X4 square grid {(x, y) : x, y ε { 0, 1, 2, 3 }}. A monotone path in this grid starts at (0, 0) and at each step either moves one unit up or one unit right. For example, from the point (x, y) one can in one step either move to (x + 1, y) ε S or (x, y + 1) ε S, but never leave S. Let the number of distinct monotone paths to reach point (2, 2) starting from (0, 0) be z. How many distinct monotone paths are there to reach point (3, 3) starting from (0, 0)?
A
2Z+6
B
3Z+6
C
2Z+8
D
3Z+8
E
3Z+4
Engineering-MathematicsCombinatorics
Question 8
A
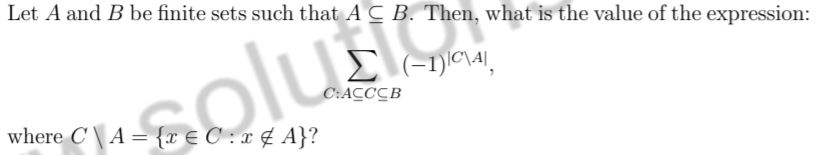
Always 0
B
Always 1
C
0 if A = B and 1 otherwise.
D
1 if A = B and 0 otherwise
E
Depends on the size of the universe
Engineering-MathematicsSet-Theory
Question 9
Suppose a rectangular farm has area 100 square metres. The lengths of its sides are not known. It is known, however, that all the edges are at least 2 metres in length. Which of the following statements about the rectangle’s perimeter p (in metres) is FALSE?
A
p can take all values between 45 and 50
B
p can be 52 for some configuration
C
p can take all values between 55 and 60
D
p can be 70 for some configuration
E
p can be 39 for some configuration
Question 10
Consider the sequence (sn : n ≥ 0) defined as follows: s0 = 0, s1 = 1, s2 = 1, and sn = sn-1 + sn-2 + sn-3, for n ≥ 3. Which of the following statements is FALSE?
A
s4k is even, for any k ≥ 0
B
s4k+1 is odd, for any k ≥ 0
C
s4k+2 is odd, for any k ≥ 0
D
sn is a multiple of 3, for only finitely many values of n
E
s4k+3 is even, for any k ≥ 0
Engineering-MathematicsCombinatorics
Question 11
In one of the islands that his travels took him to, Gulliver noticed that the probability that a (uniformly) randomly chosen inhabitant has height at least 2 metres is 0.2. Also, 0.2 is the probability that a (uniformly) randomly chosen inhabitant has height at most 1.5 metres. What can we conclude about the average height h in metres of the inhabitants of the island?
(i) 1.5 ≤ h ≤ 2
(ii) h ≥ 1.3
(iii) h ≤ 2.2
Which of the above statements is necessarily true?
A
(ii) only
B
(iii) only
C
(i), (ii), and (iii)
D
(ii) and (iii) only
E
None of the above
Engineering-MathematicsProbability-and-statistics
There are 11 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access