TIFR PHD CS & SS 2019
Question 1 |
Let X be a set with n elements. How many subsets of X have odd cardinality?
n | |
2n | |
2n/2 | |
2n-1 | |
Cannot be determined without knowing whether n is odd or even |
Question 2 |
How many proper divisors (that is, divisors other than 1 or 7200) does 7200 have?
18 | |
20 | |
52 | |
54 | |
60 |
Question 3 |
A is an nXn square matrix for which the entries in every row sum to 1. Consider the following statements:
(i) The column vector [1, 1, . . . , 1]T is an eigenvector of A.
(ii) det(A − I) = 0.
(iii) det(A) = 0.
Which of the above statements must be TRUE?
(i) The column vector [1, 1, . . . , 1]T is an eigenvector of A.
(ii) det(A − I) = 0.
(iii) det(A) = 0.
Which of the above statements must be TRUE?
Only (i) | |
Only (ii) | |
Only (i) and (ii) | |
Only (i) and (iii) | |
(i), (ii) and (iii) |
Question 4 |
What is the probability that a point P=(α,β) picked uniformly at random from the disk x2 + y2 ≤ 1 satisfies α + β ≤ 1?
1/π
| |
(3/4)+(1/4).(1/π) | |
(3/4)+(1/4).(2/π) | |
1 | |
2/π |
Question 5 |
Asha and Lata play a game in which Lata first thinks of a natural number between 1 and 1000. Asha must find out that number by asking Lata questions, but Lata can only reply by saying “yes” or “no”. Assume that Lata always tells the truth. What is the least number of questions that Asha needs to ask within which she can always find out the number Lata has thought of?
10 | |
32 | |
100 | |
999 | |
None of the above |
Question 6 |
A function f : R → R is said to be convex if for all x, y ∈ R and λ such that 0 ≤ λ ≤ 1,
f (λx + (1 − λ)y) ≤ λf (x) + (1 − λ)f (y).
Let f : R → R be a convex function, and define the following functions:
p(x) = f (−x), q(x) = −f (−x), and r(x) = f (1 − x).
Which of the functions p, q and r must be convex?
f (λx + (1 − λ)y) ≤ λf (x) + (1 − λ)f (y).
Let f : R → R be a convex function, and define the following functions:
p(x) = f (−x), q(x) = −f (−x), and r(x) = f (1 − x).
Which of the functions p, q and r must be convex?
Only p | |
Only q | |
Only r | |
Only p and r | |
Only q and r |
Question 7 |
What are the last two digits of 1! + 2! + . . . + 100!?
00 | |
13 | |
30 | |
33 | |
73 |
Question 8 |
Consider the following toy model of traffic on a straight, single lane, highway. We think of cars as points, which move at the maximum speed v that satisfies the fol- lowing constraints:
1. The speed is no more than the speed limit vmax mandated for the highway.
2. The speed is such that when travelling at this speed, it takes at least time t0 (where t0 is a fixed time representing the reaction time of drivers) to reach the car ahead, in case the car ahead stops suddenly.
Let as assume that in the steady state, all cars on the highway move at the same speed v satisfying both the above constraints, and the distance between any two successive cars is the same. Let ρ denote the “density”, that is, the number of cars per unit length of the highway. Which of the following graphs most accurately captures the relationship between the speed v and density ρ in this model?
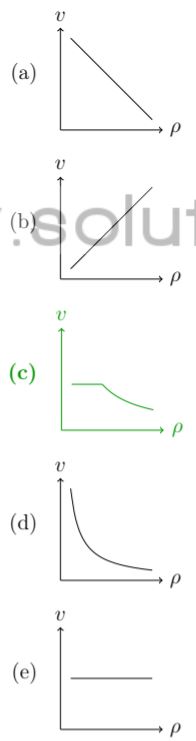
1. The speed is no more than the speed limit vmax mandated for the highway.
2. The speed is such that when travelling at this speed, it takes at least time t0 (where t0 is a fixed time representing the reaction time of drivers) to reach the car ahead, in case the car ahead stops suddenly.
Let as assume that in the steady state, all cars on the highway move at the same speed v satisfying both the above constraints, and the distance between any two successive cars is the same. Let ρ denote the “density”, that is, the number of cars per unit length of the highway. Which of the following graphs most accurately captures the relationship between the speed v and density ρ in this model?

a | |
b | |
c | |
d | |
e |
Question 9 |
Let A and B be two containers. Container A contains 50 litres of liquid X and container B contains 100 litres of liquid Y . Liquids X and Y are soluble in each other.
We now take 30ml of liquid X from container A and put it into container B. The mixture in container B is then thoroughly mixed and 20ml of the resulting mixture is put back into container A. At the end of this process let VAY be the volume of liquid Y in container A and VBX be the volume of liquid X in container B. Which of the following must be TRUE?
VAY < VBX | |
VAY > VBX | |
VAY = VBX | |
VAY + VBX = 30 | |
VAY + VBX = 20 |
Question 10 |
Avni and Badal alternately choose numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} without replacement (starting with Avni). The first person to choose numbers of which any 3 sum to 15 wins the game (for example, Avni wins if she chooses the numbers 8, 3, 5, 2, since 8 + 5 + 2 = 15). A player is said to have a winning strategy if the player can always win the game, no matter what the other player does. Which of the following statements is TRUE?
As a hint, there are exactly 8 ways in which 3 numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} can sum up to 15, shown as the three rows, the three columns, and the two diagonals in the following square:
8 1 6
3 5 7
4 9 2
As a hint, there are exactly 8 ways in which 3 numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} can sum up to 15, shown as the three rows, the three columns, and the two diagonals in the following square:
8 1 6
3 5 7
4 9 2
Avni has a winning strategy | |
Badal has a winning strategy | |
Both of them have a winning strategy | |
Neither of them has a winning strategy | |
The player that picks 9 has a winning strategy |
Question 11 |
Suppose there are n guests at a party (and no hosts). As the night progresses, the guests meet each other and shake hands. The same pair of guests might shake hands multiple times, for some parties stretch late into the night, and it is hard to keep track. Still, they don’t shake hands with themselves. Let Odd be the set of guests who have shaken an odd number of hands, and let Even be the set of guests who have shaken an even number of hands. Which of the following stays invariant throughout the night?
|Odd| mod 2 | |
|Even| | |
|Even| • |Odd| | |
2|Even| − |Odd| | |
2|Odd| − |Even| |
There are 11 questions to complete.
