GATE 1989

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Question 1

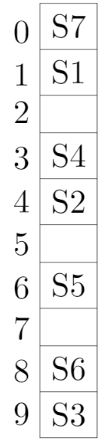
A hash table with ten buckets with one slot per bucket is shown in the following figure. The symbols S1 to S7 initially entered using a hashing function with linear probing. The maximum number of comparisons needed in searching an item that is not present is

A	4
B	5
C	6
D	3

Data-Structures Hashing

Question 1 Explanation:

In this, maximum size of cluster = 4 (S6, S3, S7, S1)
→ Worst case of finding a number is equal to maximum size of cluster + 1(after searching all the cluster it enters into empty cluster)
→ Maximum no. of comparisons = 4 + 1 = 5

Question 2

In which of the following case(s) is it possible to obtain different results for call-by-reference and call-by-name parameter passing?

A	Passing an expression as a parameter
B	Passing an array as a parameter
C	Passing a pointer as a parameter
D	Passing as array element as a parameter
E	Both A and D

Programming Parameter-Passing

Question 2 Explanation:

Option D:
Passing array element as a parameter.
Consider an example:
{
.......
a[ ] = {1, 2, 3, 4, 5}
fun (a[i]);
print a[0];
}
fun (int x)
{
int i=1;
}
O/P:
Call-by-reference: 6
Call-by-name: 1
Result is different.
Option A:
While we passing an expression as a parameter due to precedence (higher (or) lower), the output may changes.
If we pass 1+2 to the below function
int foo (int x)
{
return x*x;
}
O/P:
Call by reference = 3*3 = 9
Call by name = 1+2*1+2 (* has higher precedence e)
= 1+2+2
= 5
Output differs.
Answer: A, D

Question 3

Merging states with a common core may produce __________ conflicts and does not produce ___________ conflicts in an LALR purser.

A	Reduce-Reduce, Shift-Reduce

Compiler-Design Parsers

Question 3 Explanation:

Merge states with a common core may produce Reduce-Reduce conflicts and does not produce Shift-Reduce conflicts in an LALR parser.

Question 4

The transitive closure of the relation {(1, 2), (2, 3), (3, 4), (5, 4)} on the set {1, 2, 3, 4, 5} is ___________.

A	{(1,2), (2,3), (1,3), (3,4), (2,4), (1,4), (5,4)}

Engineering-Mathematics Sets-And-Relation

Question 4 Explanation:

Transitive closure of the relation {(1,2), (2,3), (3,4), (5,4)} = {(1,2), (2,3), (1,3), (3,4), (2,4), (1,4), (5,4)}
Transitive closure of R:
(a) It is transitive.
(b) It contains R.
(c) It is minimal, satisfies a & b.

Question 5

Match the pairs in the following questions:

(A) Cyclic redundancy code      (p) Error correction
(B) Serial communication        (q) Wired-OR
(C) Open collector              (r) Error detection
(D) Hamming code                (s) RS-232-C

A	(A)-(r), (B)-(s), (C)-(q), (D)-(p)

Computer-Organization Match-the-Following

Question 5 Explanation:

Question 6

Match the pairs in the following questions:

(A) Base addressing         (p) Reentranecy
(B) Indexed addressing      (q) Accumulator
(C) Stack addressing        (r) Array
(D) Implied addressing      (s) Position independent

A	(A)-(s), (B)-(r), (C)-(p), (D)-(q)

Computer-Organization Match-the-Following

Question 6 Explanation:

Base addressing is a position independent. By changing the value in base register, location of address also be changed.
Indexing mode can be used to access an array whose elements are in successive memory locations.
Stack addressing is a Reentranecy whenever code happens to be used again, address is need not be the same.
Implied addressing belongs to accumulator if an address is not specified, It is assumed implied to be accumulator.

Question 7

Match the pairs in the following questions:

(A) O(log n)         (p) Heapsort
(B) O(n)             (q) Depth-first search
(C) O(n log n)       (r) Binary search
(D) O(n²)            (s) Selection of the k^th smallest 
                         element in a set of n elements.

A	(A)-(r), (B)-(s), (C)-(p), (D)-(q)

Data-Structures Match-the-Following

Question 7 Explanation:

O(log n) - Binary search
O(n) - Selection of the k^th smallest element in a set of n elements
O(n log n) - Heapsort
O(n²) - Depth-first search

Question 8

Match the pairs in the following questions:

(A) Virtual memory      (p) Temporal Locality
(B) Shared memory       (q) Spatial Locality
(C) Look-ahead buffer   (r) Address Translation
(D) Look-aside buffer   (s) Mutual Exclusion

A	(A)-(r), (B)-(s), (C)-(q), (D)-(p)

Operating-Systems Match-the-Following

Question 8 Explanation:

Virtual Memory - Address Translation
Shared Memory - Mutual Exclusion
Look-ahead buffer - Spatial Locality
Look-aside buffer - Temporal Locality

Question 9

An unrestricted use of the "go to" statement is harmful because of which of the following reason(s):

A	It makes it more difficult to verify programs.
B	It makes programs more inefficient.
C	It makes it more difficult to modify existing programs.
D	It results in the compiler generating longer machine code.

Programming Programming

Question 9 Explanation:

Dijkstra's argued that unrestricted goto statements should abolished from the higher-level languages because they complicated the task of analyzing and verifying the correctness of programs.

Question 10

Context-free languages and regular languages are both closed under the operation(s) of:

A	Union
B	Intersection
C	Concatenation
D	Complementation
E	Both A and C

Theory-of-Computation Context-Free-and-Regular-Languages

Question 10 Explanation:

Regular languages closed under Union, Intersection, Concatenation and Complementation but CFC is only closed under Union and Concatenation.

Question 11

Which of the following problems are undecidable?

A	Membership problem in context-free languages.
B	Whether a given context-free language is regular.
C	Whether a finite state automation halts on all inputs.
D	Membership problem for type 0 languages.
E	Both (A) and (C).

Theory-of-Computation Undecidability

Question 11 Explanation:

→ Option A is decidable as we have various membership algorithms for CFL languages such as CYK algo, LL(K) and LC(K) parsing algorithms etc. In fact the upper bound to determine if a string belongs to CFL is given by O(n³) in worst case scenario by CYK algo and in some cases we have best case as O(n) as this is the case of S-grammar.
→ Option C is also decidable because this is a trivial problem as finite state automaton is a specific case of halting turing machine with limited power.

Question 12

Which of the following well-formed formulas are equivalent?

A	P → Q
B	¬Q → ¬P
C	¬P ∨ Q
D	¬Q → P
E	A, B and C.

Engineering-Mathematics Propositional-Logic

Question 12 Explanation:

P → Q ⇔ ¬P ∨ Q
¬Q → ¬P ⇔ Q ∨ ¬P
¬P ∨ Q ⇔ ¬P ∨ Q
¬Q → P ⇔ Q ∨ P
A, B and C are equivalent.

Question 13

Which of the following graphs is/are planner?

A	Theory Explanation is given below.

Engineering-Mathematics Graph-Theory

Question 13 Explanation:

(i) G₁ is K₃₃ which is planar graph with the minimum number of edges.
→ Let us assume K₃₃is a planar graph. Then it satisfy the useful corollary. As there is no triangle in K₃₃.
Let G be a connected planar graph with n vertices and m edges, and no triangles. Then m≤2n-4.
Where m=9, n=6
⇒ 9 ≤ 12 - 4
⇒ 9 ≤ 8, which is to be false, then K₃₃ is non-planar graph.
(ii) G₂ is a planar graph. Because it can be redrawn like as below.

(iii) Let us assume G₃ be a planar graph then it also be satisfy useful corollary.
Where m=9, n=6
then 9 ≤ 12-4
9 ≤ 8 is False
So, G₃ is non-planar graph.
Answer: Only G₂ is planar graph.

Question 14

Which of the following statements are FALSE?

A	For poisson distribution, the mean is twice the variance.
B	In queuing theory, if arrivals occur according to poisson distribution, then the inter-arrival time is exponentially distributed.
C	The distribution of waiting time is independent of the service discipline used in selecting the waiting customers for service.
D	If the time between successive arrivals is exponential, then the time between the occurrences of every third arrival is also exponential.
E	Both (A) and (C).

Engineering-Mathematics Probability

Question 14 Explanation:

In Poisson distribution, the mean is not equal to the twice the variance.
Option C is also False, because waiting time is dependent on the service discipline.

Question 15

Which one of the following statements(s) is/are FALSE?

A	Overlaying is used to run a program, which is longer than the address space of the computer.
B	Optimal binary search tree construction can be performed efficiently by using dynamic programming.
C	Depth first search cannot be used to find connected components of a graph.
D	Given the prefix and postfix walls over a binary tree, the binary tree can be uniquely constructed.
E	A, C and D.

Data-Structures True or False

Question 15 Explanation:

Option A - False
As per the definition of address space memory used by the overlay comes under the address space of computer.
Option B: True
By using dynamic programming we can construct optimal binary search tree efficiently.
Option C: False
DFS can be used to find connected components of a graph.
Option D: False
Infix + C postfix or prefix is required to construct the binary tree uniquely.

Question 16

For secondary key processing which of the following file organizations is preferred? Give a one line justification:

A	Indexed sequential file organization.
B	Two-way linked list.
C	Inverted file organization.
D	Sequential file organization.

Database-Management-System Indexing

Question 16 Explanation:

Inverted file organization, because of reasons are as follows:
→ An index for each secondary key.
→ An index entry for each distinct value of the secondary key.
→ Exhibits better enquiry performance.

There are 16 questions to complete.