GATE 2010

Please wait while the activity loads. If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Question 1

Let G = (V,E) be a graph. Define ξ(G) = Σd id x d, where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T),then

A	\|S\| = 2\|T\|
B	\|S\| = \|T\| - 1
C	\|S\| = \|T\|
D	\|S\| = \|T\| + 1

Engineering-MathematicsGraph-Theory

Question 1 Explanation:

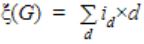
i_d= no. of vertices of degree ‘d’ in ‘G’
Eg:

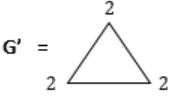
No. of vertices with degree ‘2’ = 3
ξ(G') = 3 × 2 = '6' i.e., sum of degrees
By Handshaking Theorem,
The sum of degrees would be equal to twice the no. of edges
|V| = 2|E|
It is given that ξ(G) = ξ(S) then
Sum of degrees of vertices in G is equal to sum of degrees of vertices in S
i.e., 2*(no. of edges in G) = 2*no. of edges in S no. of edges in G = no. of edges in S
Eg:

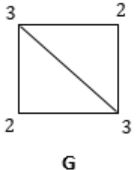
ξ(G) = (2 × 2) + (2 × 3) = 4 + 6 = 10

ξ(S) = 2 × 5 = 10
You can observe that, though no. of vertices are different, but still no. of edges are same.

Question 2

Newton-Raphson method is used to compute a root of the equation x² - 13 = 0 with 3.5 as the initial value. The approximation after one iteration is

A	3.575
B	3.676
C	3.667
D	3.607

Engineering-MathematicsNewton-Raphson-Method

Question 2 Explanation:

Note: Out of syllabus.

Question 3

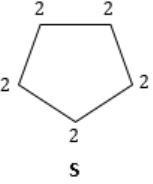
What is the possible number of reflexive relations on a set of 5 elements?

A	2¹⁰
B	2¹⁵
C	2²⁰
D	2²⁵

Engineering-MathematicsSets-And Relation

Question 3 Explanation:

Let set = ‘A’ with ‘n’ elements,
Definition of Reflexive relation:
A relation ‘R’ is reflexive if it contains xRx ∀ x∈A
A relation with all diagonal elements, it can contain any combination of non-diagonal elements.
Eg:
A={1, 2, 3}

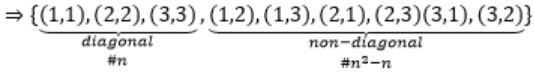
So for a relation to be reflexive, it should contain all diagonal elements. In addition to them, we can have possible combination of (n²-n)non-diagonal elements (i.e., 2^n²-n)
Ex:
{(1,1)(2,2)(3,3)} ----- ‘0’ non-diagonal element
{(1,1)(2,2)(3,3)(1,2)} ----- ‘1’ non-diagonal element
{(1,1)(2,2)(3,3)(1,2)(1,3)} “
___________ “
___________ “
{(1,1)(2,2)(3,3)(1,2)(1,3)(2,1)(2,3)(3,1)(3,2)} (n²-n) diagonal elements
____________________
Total: 2^n²-n
For the given question n = 5.
The number of reflexive relations = 2^(25-5) = 2²⁰

Question 4

Consider the set S = {1, ω, ω²}, where ω and ω² are cube roots of unity. If * denotes the multiplication operation, the structure (S,*) forms

A	A group
B	A ring
C	An integral domain
D	A field

Engineering-MathematicsSets-And Relation

Question 4 Explanation:

A Group is an algebraic structure which satisfies
1) Closure
2) Associativity
3) Have Identity element
4) Invertible
Over ‘*’ operation the S = {1, ω, ω²} satisfies the above properties.
The identity element is ‘1’ and inverse of 1 is 1, inverse of ‘w’ is 'w²' and inverse of 'w²' is 'w'.

Question 5

What is the value of

A	0
B	e^-2
C	e^-1/2
D	1

Engineering-MathematicsCalculus

Question 5 Explanation:

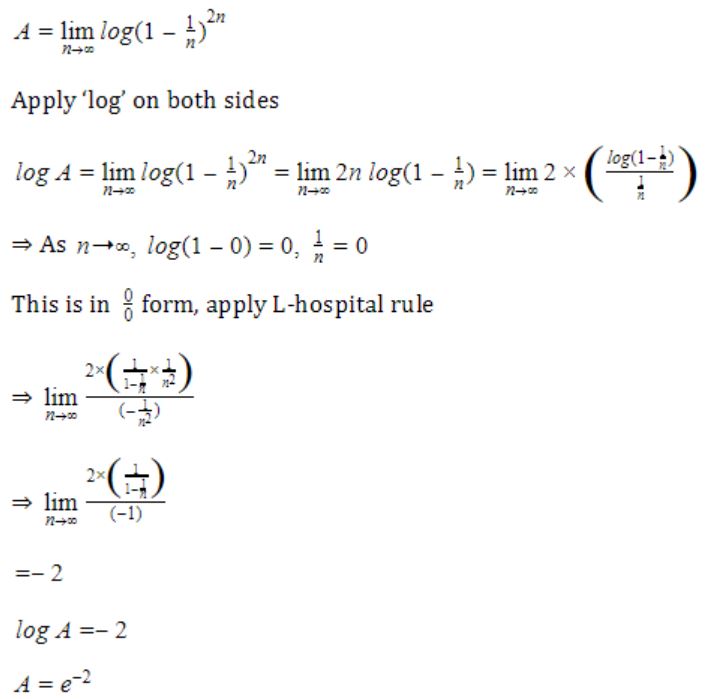
Question 6

The minterm expansion of is

A	m₂+m₄+m₆+m₇
B	m₀+m₁+m₃+m₅
C	m₀+m₁+m₆+m₇
D	m₂+m₃+m₄+m₅

Digital-Logic-DesignBoolean-Algebra

Question 6 Explanation:

Convert PQ + QR' + PR' into canonical form
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m₇ + m₆ + m₂ + m₄

Question 7

A main memory unit with a capacity of 4 megabytes is built using 1M 1-bit DRAM chips. Each DRAM chip has 1K rows of cells with 1K cells in each row. The time taken for a single refresh operation is 100 nanoseconds. The time required to perform one refresh operation on all the cells in the memory unit is

A	100 nanoseconds
B	100*2¹⁰ nanoseconds
C	100*2²⁰ nanoseconds
D	3200*2²⁰ nanoseconds

Digital-Logic-DesignMemory-Interfacing

Question 7 Explanation:

Each chip capacity = 1M x 1-bit
Required capacity = 4MB
Number of chips needed = 4M*8 bits / 1M x 1-bit = 32 (1M x 1-bit)/(1M x 1-bit) = 32
Irrespective of the number of chips, all chips can be refreshed in parallel.
And all the cells in a row are refreshed in parallel too. So, the total time for refresh will be number of rows times the refresh time of one row.
Here we have 1K rows in a chip and refresh time of single row is 100ns.
So total time required = 1K × 100
= 100 × 2¹⁰ nanoseconds

Question 8

P is a 16-bit signed integer. The 2's complement representation of P is (F87B)₁₆. The 2's complement representation of 8*P is

A	(C3D8)₁₆
B	(187B)₁₆
C	(F878)₁₆
D	(987B)₁₆

Digital-Logic-DesignNumber-Systems

Question 8 Explanation:

(F87B)₁₆ is 2's complement representation of P.
(F87B)₁₆=(1111 1000 0111 1011)₂. (It is a negative number which is in 2's complement form)
P = 1111 1000 0111 1011 (2's complement form)
8 * P = 2³* P = 1100 0011 1101 1000. ( NOTE: Left shift k times is equivalent to Multiplication by 2^k)
Hence, 1100 0011 1101 1000 is 2's complement representation of 8P.
1100 0011 1101 1000 = (C3D8)₁₆.

Question 9

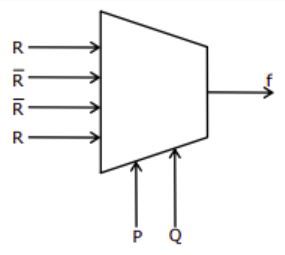
The Boolean expression for the output 'f' of the multiplexer shown below is

A
B	P⊕Q⊕R
C	P+Q+R
D

Digital-Logic-DesignMultiplexer

Question 9 Explanation:

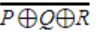f = P’Q’ R + P’Q R’ + PQ’ R’ + PQR
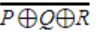= (P’Q’ + PQ)R + (P’Q+PQ’)R’
= (P⊕Q)’R + (P⊕Q)R’
= (P⊕Q⊕R)

Question 10

In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?

A	0
B	1
C	(n-1)/2
D	n-1

Data-StructuresBinary-Trees

Question 10 Explanation:

Given a Binary Tree with n nodes.
Every node has an odd number of descendants.
Also given every node is considered to be its own descendant.

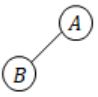
― This is even number of descendants (2), because A is also considered as a descendant.

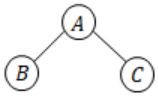
― This is odd number of descendants (3), A, B, C are descendants here.
Condition satisfied – odd number, but number of nodes in a tree that has exactly one child is 0.

Question 11

What does the following program print?

#include
void f(int *p, int *q)
{
  p = q;
 *p = 2;
}
int i = 0, j = 1;
int main()
{
  f(&i, &j);
  printf("%d %d n", i, j);
  getchar();
  return 0;
}

A	2 2
B	2 1
C	0 1
D	0 2

ProgrammingC-Programming

Question 11 Explanation:

Both pointers points to j = 1
now *p = 2
where j is updated with value 2.
printf (i, j) i = 0, j = 2

Question 12

Two alternative packages A and B are available for processing a database having 10^k records. Package A requires 0.0001n² time units and package B requires 10nlog₁₀n time units to process n records.What is the smallest value of k for which package B will be preferred over A?

A	12
B	10
C	6
D	5

AlgorithmsTime-Complexity

Question 12 Explanation:

As per given information Package B 10nlog₁₀n is lesser than or equals to Package A 0.0001n² 0 because n² is asymptotically larger than nlogn. Finally, 10nlog₁₀n ≤ 0.0001n²
Let n = 10^k records. Substitute into 10nlog₁₀n ≤ 0.0001n²
10(10^k)log₁₀10^k ≤ 0.0001(10^k)²
10^k+1k ≤ 0.0001 × 10^2k
k ≤ 10^{2k−k−1−4}
k ≤ 10^k−5
According to the problem value 6 is suitable for K.

Question 13

Which data structure in a compiler is used for managing information about variables and their attributes?

A	Abstract syntax tree
B	Symbol table
C	Semantic stack
D	Parse Table

Compiler-DesignCompilers

Question 13 Explanation:

Symbol tables are data structures that are used by compilers to hold information about source-program constructs. The information is collected incrementally by the analysis phases of a compiler and used by the synthesis phases to generate the target code. Entries in the symbol table contain information about an identifier such as its character string (or lexeme) , its type, its position in storage, and any other relevant information.

Question 14

Which languages necessarily need heap allocation in the runtime environment?

A	Those that support recursion
B	Those that use dynamic scoping
C	Those that allow dynamic data structures
D	Those that use global variables

Compiler-DesignRun-Time-Environment

Question 14 Explanation:

Dynamic memory is allocated on the heap by the system. So the languages which allow dynamic data structure require heap allocation at runtime.

Question 15

One of the header fields in an IP datagram is the Time to Live (TTL) field. Which of the following statements best explains the need for this field?

A	It can be used to prioritize packets
B	It can be used to reduce delays
C	It can be used to optimize throughput
D	It can be used to prevent packet looping

Computer-NetworksIP-Packet

Question 15 Explanation:

Time to Live (TTL) is a limit on the period of time or transmissions in computer and computer network technology that a unit of data (e.g. a packet) can experience before it should be discarded. If the limit is not defined then the packets can go into an indefinite loop. The packet is discarded when the Time to Live field reaches 0 to prevent looping.

Question 16

Which one of the following is not a client server application?

A	Internet chat
B	Web browsing
C	E-mail
D	ping

Computer-NetworksClient-Server-Computing

Question 16 Explanation:

Ping is used for knowing status of a host by another host. it is not a client server application.

There are 16 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access

A	\|S\| = 2\|T\|
B	\|S\| = \|T\| - 1
C	\|S\| = \|T\|
D	\|S\| = \|T\| + 1