GATE 2015 [Set-2]
Question 1 |
Based on the given statements, select the most appropriate option to solve the given question, What will be the total weight of 10 poles each of same weight?
-
Statements:
(I) One fourth of the weight of a pole is 5 kg
(II) The total weight of these poles is 160 kg more than the total weight of two poles.
Statement I alone is not sufficient | |
Statement II alone is not sufficient | |
Statement II alone is not sufficient | |
Both statements I and II together are not sufficient. |
One fourth of the weight of a pole is 5Kg. ⇒ Weight of pole is 4×5 = 20Kg
Weight of 10 poles each of same weight = 10×20 = 200 Kg
∴Statement I alone is sufficient.
Statement-II:
Let, Weight of each pole = W Kg
Given,
10W = 2W + 160
⇒ 8W = 160
W = 20Kg
∴ Weight of each pole = 20 Kg
∴ Weight of 10 poles = 10×20 Kg = 200 Kg
∴ Statement II alone is sufficient.
Option (C) is the answer.
Either I or II alone is sufficient.
Question 2 |
Consider a function f(x) = 1 - |x| on -1 ≤ x ≤ 1. The value of x at which the function attains a maximum and the maximum value of the function are
0, -1 | |
-1, 0 | |
0, 1 | |
-1, 2 |
In the given function, it is given as
-|x| ⇒ To obtain the maximum of this function we have to minimize the value -|x| and the minimum value is 0.
∴ Maximum value of f(x) is at f(0) and i.e., f(x) = 1
Maximum value is 1 at x=0.
Question 3 |
A generic term that include various items of clothing such as a skirt, a pair of trousers and a shirt is
fabric | |
textile | |
fibre | |
apparel |
Question 4 |
Choose the statement where underlined word is used correctly.
The industrialist load a personnel jet.
| |
I write my experience in my personnel diary. | |
All personnel are being given the day off. | |
Being religious is a personnel aspect. |
Question 5 |
We __________________ our friend’s birthday and we ______________ how to make it up to him.
Completely forgot - - - don’t just know
| |
Forgot completely - - - don’t just know | |
Completely forgot - - - just don’t know | |
Forgot completely - - - just don’t know |
Question 6 |
In a triangle PQR, PS is the angle bisector of ∠QPR and ∠QPS = 60º. What is the length of PS?
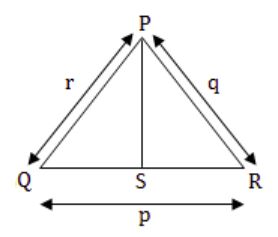
(q+r)/qr | |
qr/(q+r) | |
√(q2 + r2) | |
(q+r)2 /qr |
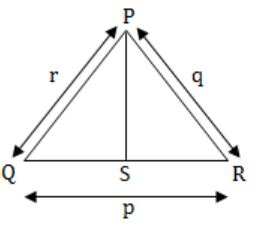
∠QPS = 60º
and PS is angle bisector of ∠QPR
⇒ ∠QPS = ∠SPR = 60º
and ∠QPR = 120º
Let, PS = s
Area of ΔPQR = Area of ΔPQS + Area of ΔSPR
1/2 qr Sin∠QPR = 1/2 rs Sin∠QPS + 1/2 sq∠SPR
1/2 qr Sin 120º = 1/2 rs Sin 60º + 1/2 sq 60º
1/2 qr Sin × √3/2 = 1/2 rs × √3/2 + 1/2 × √3/2
qr = rs + sq
∴ s = qr/q+r
PS = qr/q+r
Question 7 |
Out of the following four sentences, select the most suitable sentence with respect to grammar and usage.
Since the report lacked needed information, it was of no use to them.
| |
The report was useless to them because there were no needed information in it.
| |
Since the report did not contain the needed information, it was not real useful to them | |
Since the report lacked needed information, it would not have been useful to them. |
(C) not really useful
(D) would not have been
Question 8 |
If the list of letters, P, R, S, T, U is an arithmetic sequence, which of the following are also in arithmetic sequence?
-
I. 2P, 2R, 2S, 2T, 2U
II. P-3, R-3, S-3, T-3, U-3
III. P2, R2, S2, T2, U2
I only | |
I and II | |
II and III | |
I and III |
Hence, II is an arithmetic sequence.
If the set of numbers is multiplied by the common number, even then the new set will also be in arithmetic sequence.
Hence, I is an arithmetic sequence.
Question 9 |
If p, q, r, s are distinct integers such that:
-
f(p,q,r,s) = max(p,q,r,s)
g(p,q,r,s) = min(p,q,r,s)
h(p,q,r,s) = remainder of (p×q)(r×s) if (p×q)>(r×s) OR remainder of (r×s)(p×q) if (r×s)>(p×q)
Also a function fgh(p,q,r,s) = f(p,q,r,s) × g(p,q,r,s) ×h(p,q,r,s)
Also the same operations are valid with two variable functions of the form f(p,q).
What is the value of fg(h(2,5,7,3),(4,6,8)?
8 | |
9 | |
7 | |
6 |
= remainder of 21/10
= 1
fg(1,4,6,8) = f(1,4,6,8) × g(1,4,6,8)
= max(1,4,6,8) × min(1,4,6,8)
= 8 × 1
= 8
Question 10 |
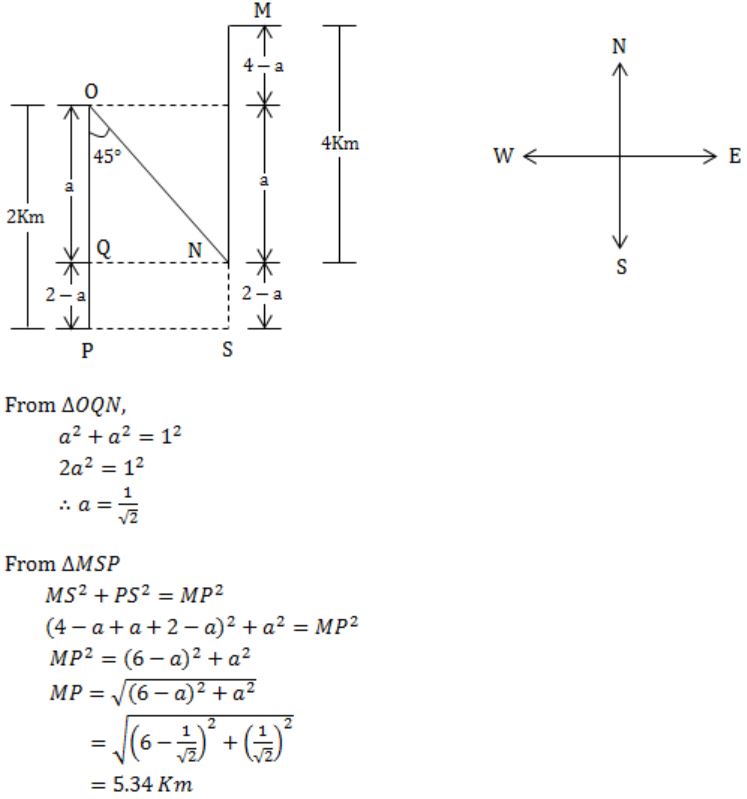
Four branches of a company are located at M, N, O and P. M is north of N at a distance of 4km; P is south of O at a distance of 2 km; N is southeast of O by 1 km. What is the distance between M and P in km?
5.34 | |
6.74 | |
28.5 | |
45.49 |
Question 11 |
An unordered list contains n distinct elements. The number of comparisons to find an element in this list that is neither maximum nor minimum is
Θ(nlog n) | |
Θ(n) | |
Θ(log n) | |
Θ(1) |
Question 12 |
Let R be the relation on the set of positive integers such that aRb if and only if a and b are distinct and have a common divisor other than 1. Which one of the following statements about R is true?
R is symmetric and reflexive but not transitive | |
R is reflexive but not symmetric and not transitive | |
R is transitive but not reflexive and not symmetric | |
R is symmetric but not reflexive and not transitive |
In aRb, 'a' and 'b' are distinct. So it can never be reflexive.
Symmetric:
In aRb, if 'a' and 'b' have common divisor other than 1, then bRa, i.e., 'b' and 'a' also will have common divisor other than 1. So, yes symmetric.
Transitive:
Take (3, 6) and (6, 2) elements of R. For transitivity (3, 2) must be the element of R, but 3 and 2 don't have a common divisor. So not transitive.
Question 13 |
Consider the following transaction involving two bank account x and y.
read(x); x:= x-50; write(x); read(y); y:= y+50; write(y)The constraint that the sum of the accounts x and y should remain constant is that of
Atomicity | |
Consistency | |
Isolation | |
Durability |
Question 14 |
A binary tree T has 20 leaves. The number of nodes in T having two children is _________.
19 | |
20 | |
21 | |
22 |
(i) p vertices (i.e., leaves) of degree 1
(ii) one vertex (i.e., root of T) of degree 2
(iii) 'n - p - 1' (i.e., interval) vertices of degree 3
(iv) n - 1 edges
∴ By Handshaking theorem,
p × 1 + 1 × 2 + (n - p - 1) × 3 = 2(n - 1)
⇒n = 2p - 1
= 39 as p = 20
∴ n - p = 19 vertices have exactly two children
Question 15 |
Consider the basic COCOMO model where E is the effort applied in person-months, D is the development time in chronological months, KLOC is the estimated number of delivered lines of code (in thousands) and ab, bb, cb, db have their usual meanings. The basic COCOMO equations are of the form
E = a b(KLOC)exp (b b, D = c b(E)exp (d b) | |
E = a b(KLOC)exp (b b, D = c b(E)exp (d b) | |
E = a bexp(b b), D = c b(KLOC)exp (d b) | |
E = a bexp(D b), D = c b(KLOC)exp (b b) |
Effort applied (E) = ab(KLOC)bb
Development time (D) = cb(E)db
Question 16 |
Consider the following statements:
-
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected.
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
If a person is known to corrupt, he is kind | |
If a person is not known to be corrupt, he is not kind
| |
If a person is kind, he is not known to be corrupt
| |
If a person is not kind, he is not known to be corrupt |
q: candidate will be elected
r: candidate is kind
then S1 = p→~q
= q→~p (conrapositive rule)
and S2: r→q ⇒ r→~p (transitive rule)
i.e., If a person is kind, he is not known to be corrupt. ∴ Option is C
![GATE 2015 [Set-2]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)