GATE 2016 [Set-2]
Question 1 |
The man who is now Municipal Commissioner worked as _______________.
the security guard at a university | |
a security guard at the university | |
a security guard at university | |
the security guard at the university |
And coming to university it is an organization.
So we use are 'the' before university.
Question 2 |
Nobody knows how the Indian cricket team is going to cope with the difficult and seamer-friendly wickets in Australia.
Choose the option which is closest in meaning to the underlined phrase in the above sentence.
put up with | |
put in with | |
put down to | |
put up against |
→ Cope with is doesn't means that put someone into competition with some other.
Question 3 |
Find the odd one in the following group of words.
-
mock, deride, praise, jeer
mock | |
deride | |
praise | |
jeer |
Deride = express contempts for; ridicule
Jeer = Make rude and mocking remarks
→ These three are negative things
Praise = express warm approval
Question 4 |
Pick the odd one from the following options.
CADBE | |
JHKIL | |
XVYWZ | |
ONPMQ |
But in D, 2nd and 4th are in decreasing order.
Question 5 |
In a quadratic function, the value of the product of the roots (α, β) is 4. Find the value of
n4 | |
4n | |
22n-1 | |
4n-1 |
Product of roots (α, β) = 4
⇒ αβ = 4

(αβ)n = 4n
Question 6 |
Among 150 faculty members in an institute, 55 are connected with each other through Facebook® and 85 are connected through WhatsApp®. 30 faculty members do not have Facebook® or WhatsApp® accounts. The number of faculty members connected only through Facebook® accounts is ______________.
35 | |
45 | |
65 | |
90 |
Number of faculty members connected through Facebook = 55
Number of faculty members connected through Whatsapp = 85
Number of faculty members with Facebook (or) Whatsapp accounts = 30
Number of faculty members with either Facebook (or) Whatsapp accounts = 150 - 30 = 120
Number of faculty members with both Facebook and Whatsapp accounts = 85 + 55 - 120 = 20
Number of faculty members with only Facebook accounts = 55 - 20 = 35
Question 7 |
Computers were invented for performing only high-end useful computations. However, it is no understatement that they have taken over our world today. The internet, for example, is ubiquitous. Many believe that the internet itself is an unintended consequence of the original invention. With the advent of mobile computing on our phones, a whole new dimension is now enabled. One is left wondering if all these developments are good or, more importantly, required.
Which of the statement(s) below is/are logically valid and can be inferred from the above paragraph?
-
(i) The author believes that computers are not good for us.
(ii) Mobile computers and the internet are both intended inventions.
(i) only | |
(ii) only | |
both (i) and (ii) | |
neither (i) nor (ii) |
So, statement I does not follow.
→ "Many believes that the internet itself is unintended consequence of the original invention.
So, statement II does not follow, so Answer is Option D.
Question 8 |
All hill-stations have a lake. Ooty has two lakes.
Which of the statement(s) below is/are logically valid and can be inferred from the above sentences?
-
(i) Ooty is not a hill-station.
(ii) No hill-station can have more than one lake.
(i) only | |
(ii) only | |
both (i) and (ii) | |
neither (i) nor (ii) |
All hill-stations have a lake → (1)
Ooty has two lakes → (2)
From (1), it cannot be inferred that every place having a lake is a hill station.
⇒ (i) cannot be logically intended.
From (1), it cannot be inferred how many lakes will be there in a hill station.
⇒ (ii) cannot be logically inferred.
Question 9 |
In a 2 × 4 rectangle grid shown below, each cell is a rectangle. How many rectangles can be observed in the grid?
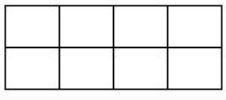
21 | |
27 | |
30 | |
36 |
Question 10 |
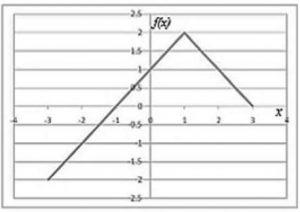
Choose the correct expression for f(x) given in the graph.
f(x) = 1 - |x - 1| | |
f(x) = 1 + |x - 1| | |
f(x) = 2 - |x - 1| | |
f(x) = 2 + |x - 1| |
x = -1 ⇒ f(x) = 0
x = 0 ⇒ f(x) = 1
We have check, which option satisfies both the conditions.
Only option (C) satisfies both of them.
Question 11 |
(i) false
(ii) Q
(iii) true
(iv) P ∨ Q
(v) ¬Q ∨ P
The number of expressions given above that are logically implied by P ∧ (P ⇒ Q) is _________.
4 | |
5 | |
6 | |
7 |
(P ∧ (P → Q))→ expression is a tautology. So we have to find
How many tautological formulas are there for the given inputs.
(P ∧ (P → Q)) → True is always tautology
(P ∧ (P → Q)) → False is not a tautology
(P ∧ (P → Q)) → Q is a tautology
(P ∧ (P → Q)) → ¬Q ∨ P is a tautology
(P ∧ (P → Q)) → P ∨ Q is a tautology
So there are 4 expressions logically implied by (P ∧ (P → Q))
Question 12 |
Let f(x) be a polynomial and g(x) = f'(x) be its derivative. If the degree of (f(x) + f(-x)) is 10, then the degree of (g(x) - g(-x)) is __________.
9 | |
10 | |
11 | |
12 |
It is given that f(x) + f(-x) degree is 10.
It means f(x) is a polynomial of degree 10.
Then obviously the degree of g(x) which is f’(x) will be 9.
Question 13 |
The minimum number of colours that is sufficient to vertex-colour any planar graph is ________.
4 | |
5 | |
6 | |
7 |
Here it is asked about the sufficient number of colors, so with the worst case of 4 colors we can color any planar graph.
Question 14 |
I. If m < n, then all such systems have a solution
II. If m > n, then none of these systems has a solution
III. If m = n, then there exists a system which has a solution
Which one of the following is CORRECT?
I, II and III are true | |
Only II and III are true | |
Only III is true | |
None of them is true |
If R(A) ≠ R(A|B)
then there will be no solution.
ii) False, because if R(A) = R(A|B),
then there will be solution possible.
iii) True, if R(A) = R(A|B),
then there exists a solution.
Question 15 |
Suppose that a shop has an equal number of LED bulbs of two different types. The probability of an LED bulb lasting more than 100 hours given that it is of Type 1 is 0.7, and given that it is of Type 2 is 0.4. The probability that an LED bulb chosen uniformly at random lasts more than 100 hours is _________.
0.55 | |
0.56 | |
0.57 | |
0.58 |
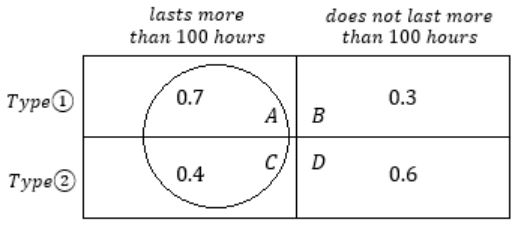
The bulbs of Type 1, Type 2 are same in number.
So, the probability to choose a type is 1/2.
The probability to choose quadrant ‘A’ in diagram is
P(last more than 100 hours/ type1) = 1/2 × 0.7
P(last more than 100 hours/ type2) = 1/2 × 0.4
Total probability = 1/2 × 0.7 + 1/2 × 0.4 = 0.55
Question 16 |
Suppose that the eigenvalues of matrix A are 1, 2, 4. The determinant of (A-1)T is _________.
0.125 | |
0.126 | |
0.127 | |
0.128 |
Given that eigen values are 1, 2, 4.
So, its determinant is 1*2*4 = 8
The determinant of (A-1)T = 1/ AT = 1/|A| = 1/8 = 0.125
![GATE 2016 [Set-2]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)