Nielit Scientist-B CS 22-07-2017
Question 1 |
What does the following functions do for a given Linked list with first node as head?
void fun1(Struct node* head)
{
if(head==NULL)
return;
fun1(head → next);
printf("%d".head → data);
}
void fun1(Struct node* head)
{
if(head==NULL)
return;
fun1(head → next);
printf("%d".head → data);
}
Prints all nodes of linked lists | |
Prints all nodes of linked list in reverse order | |
Prints alternate nodes of Linked List | |
Prints alternate nodes in reverse order |
Question 1 Explanation:
Given pointer to the head node of a linked list, the task is to reverse the linked list. We need to reverse the list by changing links between nodes.
Input : Head of following linked list
1->2->3->4->NULL
Output : Linked list should be changed to,
4->3->2->1->NULL
Algorithm:
1. Initialize three pointers prev as NULL, curr as head and next as NULL.
2. Iterate through the linked list. In loop, do following.
// Before changing next of current,
// store next node
next = curr->next
// Now change next of current
// This is where actual reversing happens
curr->next = prev
// Move prev and curr one step forward
prev = curr
curr = next
Input : Head of following linked list
1->2->3->4->NULL
Output : Linked list should be changed to,
4->3->2->1->NULL
Algorithm:
1. Initialize three pointers prev as NULL, curr as head and next as NULL.
2. Iterate through the linked list. In loop, do following.
// Before changing next of current,
// store next node
next = curr->next
// Now change next of current
// This is where actual reversing happens
curr->next = prev
// Move prev and curr one step forward
prev = curr
curr = next
Question 2 |
Which of the following statements is/are TRUE for an undirected graph?
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even
P only | |
Q only | |
Both P and Q | |
Neither P nor Q |
Question 2 Explanation:
Euler’s Theorem 3:
The sum of the degrees of all the vertices of a graph is an even number (exactly twice the number of edges).
In every graph, the number of vertices of odd degree must be even.
The sum of the degrees of all the vertices of a graph is an even number (exactly twice the number of edges).
In every graph, the number of vertices of odd degree must be even.
Question 3 |
Consider the following function that takes reference to head of a Doubly Linked List as parameter. Assume that a node of doubly linked list has previous pointer as prev and next pointer as next
void fun(struct node **head_ref)
{
struct node *temp=NULL;
Struct node *current=*head_ref;
while(current!=NULL)
{
temp=current → prev;
Current → prev=current → next;
Current → next=temp;
current=current → prev;
}
if(temp!=NULL)
*head_ref=temp → prev;
}
Assume that reference of head of following doubly linked list is passed to above function 1 <--> 2 <--> 3 <--> 4<--> 5 <--> 6. What should be the modified linked list after the function call?
void fun(struct node **head_ref)
{
struct node *temp=NULL;
Struct node *current=*head_ref;
while(current!=NULL)
{
temp=current → prev;
Current → prev=current → next;
Current → next=temp;
current=current → prev;
}
if(temp!=NULL)
*head_ref=temp → prev;
}
Assume that reference of head of following doubly linked list is passed to above function 1 <--> 2 <--> 3 <--> 4<--> 5 <--> 6. What should be the modified linked list after the function call?
1<-->2<-->4<-->3<-->6<-->5 | |
5<-->4<-->3<-->2<-->1<-->6 | |
6<-->5<-->4<-->3<-->2<-->1 | |
6<-->5<-->4<-->3<-->1<-->2 |
Question 3 Explanation:
Struct node *current=*head_ref; ---> This statement meant for storing start of linked list onto current pointer.
while(current!=NULL)
{
temp=current → prev;
Current → prev=current → next;
Current → next=temp;
current=current → prev;
}
The loop meant for traversing the entire list till to end by changing prev and next pointers of all nodes.
Change prev of the head (or start) and change the head pointer in the end.
while(current!=NULL)
{
temp=current → prev;
Current → prev=current → next;
Current → next=temp;
current=current → prev;
}
The loop meant for traversing the entire list till to end by changing prev and next pointers of all nodes.
Change prev of the head (or start) and change the head pointer in the end.
Question 4 |
Let A be a square matrix of size nxn. consider the following program. What is the expected output?
C=100
for i=1 to n do
for j=1 to n do
{
Temp=A[i][j]+C
A[i][j]=A[j][i]
A[j][i]=Temp-C
}
for i=1 to n do
for j=1 to n do
output(A[i][j]);
C=100
for i=1 to n do
for j=1 to n do
{
Temp=A[i][j]+C
A[i][j]=A[j][i]
A[j][i]=Temp-C
}
for i=1 to n do
for j=1 to n do
output(A[i][j]);
The matrix A itself | |
Transpose of matrix A | |
Adding 100 to the upper diagonal elements and subtracting 100 from diagonal elements of A | |
None of the option |
Question 4 Explanation:
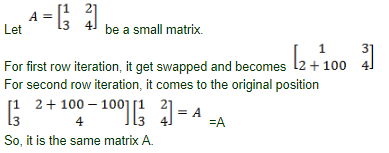
Question 5 |
Following is C like Pseudo code of a function that takes a number as an argument, and uses a stack S to do argument, and uses a stack S to do processing.
void fun(int n)
{
Stack s;//Say it creates an empty stack S
while(n>0)
{
// This line pushes the value of n%2 to
Stack S;
Push(&S,n%2);
n=n/2l
}
// Run while Stack S is not empty
while(!is Empty(&S)) Printf(%d",pop(&S));//pop an element from S and print it
}
What does the above function do in general order
void fun(int n)
{
Stack s;//Say it creates an empty stack S
while(n>0)
{
// This line pushes the value of n%2 to
Stack S;
Push(&S,n%2);
n=n/2l
}
// Run while Stack S is not empty
while(!is Empty(&S)) Printf(%d",pop(&S));//pop an element from S and print it
}
What does the above function do in general order
Prints binary representation of n in reverse order | |
prints binary representation of n | |
Prints the value of Logn | |
Prints the value of Logn in reverse order |
Question 5 Explanation:
For any number, we can check whether its ‘i’th bit is 0(OFF) or 1(ON) by bitwise ANDing it with “2^i” (2 raise to i).,
1) Let us take number 'NUM' and we want to check whether it's 0th bit is ON or OFF
bit = 2 ^ 0 (0th bit)
if NUM & bit == 1 means 0th bit is ON else 0th bit is OFF
2) Similarly if we want to check whether 5th bit is ON or OFF
bit = 2 ^ 5 (5th bit)
if NUM & bit == 1 means its 5th bit is ON else 5th bit is OFF.
Let us take unsigned integer (32 bit), which consist of 0-31 bits. To print binary representation of unsigned integer, start from 31th bit, check whether 31th bit is ON or OFF, if it is ON print “1” else print “0”. Now check whether 30th bit is ON or OFF, if it is ON print “1” else print “0”, do this for all bits from 31 to 0, finally we will get binary representation of number. void bin(unsigned n)
{
unsigned i;
for (i = 1 << 31; i > 0; i = i / 2)
(n & i)? printf("1"): printf("0");
}
int main(void)
{
bin(7);
printf("\n");
bin(4);
}
1) Let us take number 'NUM' and we want to check whether it's 0th bit is ON or OFF
bit = 2 ^ 0 (0th bit)
if NUM & bit == 1 means 0th bit is ON else 0th bit is OFF
2) Similarly if we want to check whether 5th bit is ON or OFF
bit = 2 ^ 5 (5th bit)
if NUM & bit == 1 means its 5th bit is ON else 5th bit is OFF.
Let us take unsigned integer (32 bit), which consist of 0-31 bits. To print binary representation of unsigned integer, start from 31th bit, check whether 31th bit is ON or OFF, if it is ON print “1” else print “0”. Now check whether 30th bit is ON or OFF, if it is ON print “1” else print “0”, do this for all bits from 31 to 0, finally we will get binary representation of number. void bin(unsigned n)
{
unsigned i;
for (i = 1 << 31; i > 0; i = i / 2)
(n & i)? printf("1"): printf("0");
}
int main(void)
{
bin(7);
printf("\n");
bin(4);
}
Question 6 |
Assume that the operators +,-,x are left associative and 6 right associative. the order of precedence(from highest to lowest) is 6,x,+,-. The postfix expression corresponding to the infix expression a+bxc-d^e^f is
abc x+def^^- | |
abc xde^f^- | |
ab +c xd -e^f ^ | |
-+ a x bc ^^def |
Question 6 Explanation:
a+bc-d^e^f
⟶ left to right
Step 1: abc+

⟶ left to right
Step 1: abc+
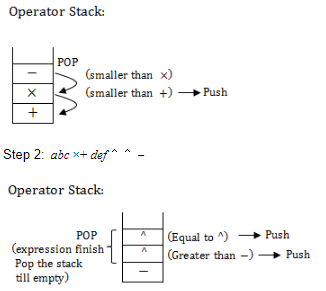
Question 7 |
A balance factor in AVL tree is used to check
What rotation to make | |
if all childs nodes are at same level | |
when the last rotation occurred | |
if the tree is unbalanced |
Question 7 Explanation:
It is a self balancing tree with height difference at most 1. A balance factor in AVL tree is used to check what rotation to make.
Question 8 |
A priority queue is implemented as a Max-heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10,8,5,3,2. Two new elements 1 and 7 are inserted into the heap in that order. The level-order traversal of the heap after the insertion of the elements is
10,8,7,3,2,1,5 | |
10,8,7,2,3,1,5 | |
10,8,7,1,2,3,5 | |
10,8,7,5,3,2,1 |
Question 8 Explanation:
Max-Heap has 5 elements:
 The level order traversal in this max heap final is:
The level order traversal in this max heap final is:
10, 8, 7, 3, 2, 1, 5.
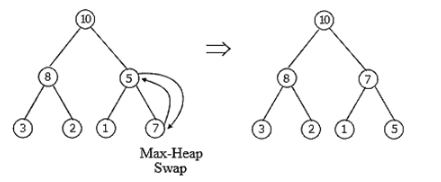 The level order traversal in this max heap final is:
The level order traversal in this max heap final is:10, 8, 7, 3, 2, 1, 5.
Question 9 |
The worst case running times of insertion sort, merge sort and quick sort respectively are
O(nlogn),O(nlogn) and O(n2) | |
O(n2),O(n2) and O(nlogn) | |
O(n2),O(nlogn) and O(nlogn) | |
O(n2),O(nlogn) and O(n2) |
Question 9 Explanation:
→ worst case running times of insertion sort → O(n2)
merge sort → O(nlogn)
quick sort → O(n2)
merge sort → O(nlogn)
quick sort → O(n2)
Question 10 |
A queue is implemented using an array such that ENQUEUE and DEQUEUE operations are performed efficiently. Which one of the following statements is CORRECT(n refers to the number of items in the QUEUE)?
Both operations can be performed in O(1) time |
Question 10 Explanation:
Since it is mentioned in the question that both of the operations are performed efficiently. Hence even the worst case time complexity will be O(1) by the use of the Circular queue there won't be any need of shifting in the array.
Question 11 |
Consider the following graph L and find the bridges, if any.


No bridges | |
{d,e} | |
{c,d} | |
{c,d} and {c,f} |
Question 11 Explanation:
A bridge, ut-edge, or cut arc is an edge of a graph whose deletion increases its number of connected components.
Equivalently, an edge is a bridge if and only if it is not contained in any cycle.
A graph is said to be bridgeless or isthmus-free if it contains no bridges.
If we remove {d,e} edge then there is no way to reach e and the graph is disconnected.
The removal of edges {c,d} and {c,f} makes graph disconnect but this forms a cycle.
Equivalently, an edge is a bridge if and only if it is not contained in any cycle.
A graph is said to be bridgeless or isthmus-free if it contains no bridges.
If we remove {d,e} edge then there is no way to reach e and the graph is disconnected.
The removal of edges {c,d} and {c,f} makes graph disconnect but this forms a cycle.
Question 12 |
The following graph nas no Euler circuit because

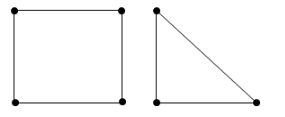
It has 7 vertices | |
It is even-valent(all vertices have even valence) | |
It is not connected | |
It does not have a Euler circuit |
Question 12 Explanation:
An Eulerian trail or Euler walk in an undirected graph is a walk that uses each edge exactly once. If such a walk exists, the graph is called traversable or semi-eulerian.
Important Properties:
→ An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
→ An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
→ An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component.
→ A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.
→ A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph
Important Properties:
→ An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
→ An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
→ An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component.
→ A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.
→ A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph
Question 13 |
For the graph shown, which of the following paths is a Hamilton circuit?

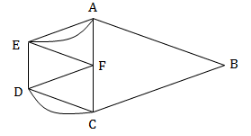
ABCDCFDEFAEA | |
AEDCBAF | |
AEFDCBA | |
AFCDEBA |
Question 13 Explanation:
A Hamiltonian cycle, also called a Hamiltonian circuit, Hamilton cycle, or Hamilton circuit, is a graph cycle (i.e., closed loop) through a graph that visits each node exactly once. A graph possessing a Hamiltonian cycle is said to be a Hamiltonian graph.
Here, Option A: A,F and E are repeated several times.
Option B: It is not a cycle. It means, not closed walk
Option C: It is closed walk and all vertex traversed. So this is final answer.
Option D: It’s not a closed walk.
Here, Option A: A,F and E are repeated several times.
Option B: It is not a cycle. It means, not closed walk
Option C: It is closed walk and all vertex traversed. So this is final answer.
Option D: It’s not a closed walk.
Question 14 |
If G is an undirected planar graph on n vertices with e edges then
e<=n | |
e<=2n | |
e<=en | |
None of the option |
Question 14 Explanation:
Euler's formula: states that if a finite, connected, planar graph is drawn in the plane without any edge intersections, and v is the number of vertices, e is the number of edges and f is the number of faces (regions bounded by edges, including the outer, infinitely large region), then
v − e + f = 2.
→ For a simple, connected, planar graph with v vertices and e edges and faces, the following simple conditions hold for v ≥ 3:
Theorem 1. e ≤ 3v − 6;
Theorem 2. If there are no cycles of length 3, then e ≤ 2v − 4.
Theorem 3. f ≤ 2v − 4.
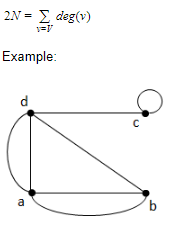
Theorem (The handshaking theorem):
Let G be an undirected graph (or multigraph) with V vertices and N edges. Then

Exercise:
Suppose a simple graph has 15 edges, 3 vertices of degree 4, and all others of degree 3. How many vertices does the graph have?
3*4+(x-3)*3=30
v − e + f = 2.
→ For a simple, connected, planar graph with v vertices and e edges and faces, the following simple conditions hold for v ≥ 3:
Theorem 1. e ≤ 3v − 6;
Theorem 2. If there are no cycles of length 3, then e ≤ 2v − 4.
Theorem 3. f ≤ 2v − 4.
Theorem (The handshaking theorem):
Let G be an undirected graph (or multigraph) with V vertices and N edges. Then
Exercise:
Suppose a simple graph has 15 edges, 3 vertices of degree 4, and all others of degree 3. How many vertices does the graph have?
3*4+(x-3)*3=30
There are 14 questions to complete.
