TIFR PHD CS & SS 2015
Question 1 |
Consider a 6-sided die with all sides not necessarily equally likely such that probability of an even number is P({2,4,6})=1/2, probability of a multiple of 3 is P({3,6})=1/3, and probability of 1 is P({1})=1/6. Given the above conditions, choose the strongest (most stringent) condition of the following that must always hold about P({5}), the probability of 5
P({5})=1/6 | |
P({5})≥1/6 | |
P({5})≤1/6 | |
P({5})≤1/3 | |
None of the above |
Question 2 |
Consider a circle with a circumference of one unit length. Let d < 1/6. Suppose that we independently throw two arcs, each of length d, randomly on this circumference so that each arc is uniformly distributed along the circle circumference. The arc attaches itself exactly to the circumference so that arc of length d exactly covers length d of the circumference. What can be said about the probability that the two arcs do not intersect each other?
It equals (1 — d) | |
It equals (1 — 3d) | |
It equals (1 — 2d) | |
It equals 1 | |
It equals (1 — d)(1 — d) |
Question 3 |
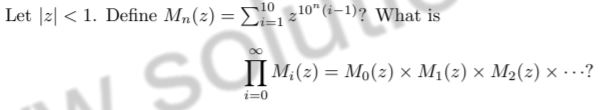
Can’t be determined | |
1/(1 - z) | |
1/(1 + z) | |
1 - z9 | |
None of the above |
Question 4 |
The Boolean function obtained by adding an inverter to each and every input of an AND gate is:
OR | |
XOR | |
NAND | |
NOR | |
None of the above |
Question 5 |
What is logically equivalent to “If Kareena and Parineeti go to the shopping mall then it is raining”:
If Kareena and Parineeti do not go to the shopping mall then it is not raining. | |
If Kareena and Parineeti do not go to the shopping mall then it is raining. | |
If it is raining then Kareena and Parineeti go to the shopping mall. | |
If it is not raining then Kareena and Parineeti do not go to the shopping mall. | |
None of the above |
Question 6 |
Ram has a fair coin, i.e., a toss of the coin results in either head or tail and each event happens with probability exactly half (1/2). He repeatedly tosses the coin until he gets heads in two consecutive tosses. The expected number of coin tosses that Ram does is
2 | |
4 | |
6 | |
8 | |
None of the above |
Question 7 |
A 1 X 1 chessboard has one (1) square, a 2 X 2 chessboards has five (5) squares. Continuing along this fashion, what is the number of squares on the (regular) 8 X 8 chessboard?
64 | |
65 | |
204 | |
144 | |
256 |
Question 8 |
There is a set of 2n people: n male and n female. A good party is one with equal number of males and females (including the one where none are invited). The total number of good parties is
2n | |
n2 | |
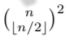 | |
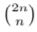 | |
none of the above |
Question 9 |
Consider a square of side length 2. We throw five points into the square. Consider the following statements:
(i) There will always be three points that lie on a straight line.
(ii) There will always be a line connecting a pair of points such that two points lie on one side of the line and one point on the other.
(iii) There will always be a pair of points which are at distance at most √2 from each other.
Which of the above is true:
(i) There will always be three points that lie on a straight line.
(ii) There will always be a line connecting a pair of points such that two points lie on one side of the line and one point on the other.
(iii) There will always be a pair of points which are at distance at most √2 from each other.
Which of the above is true:
(i) only | |
(ii) only | |
(iii) only | |
(ii) and (iii) | |
None of the above |
Question 10 |

a | |
b | |
c | |
d | |
e |
Question 11 |
Suppose that f(x) is a continuous function such that 0.4 ≤ f(x) ≤ 0.6 for 0 ≤ x ≤ 1. Which of the following is always true?
f(0.5) = 0.5 | |
There exists x between 0 and 1 such that f(x) = 0.8x | |
There exists x between 0 and 0.5 such that f(x) = x. | |
f(0.5) > 0.5. | |
None of the above statements are always true. |
There are 11 questions to complete.
