UGC NET CS 2016 July- paper-2
Question 1 |
How many different equivalence relations with exactly three different equivalence classes are there on a set with five elements?
10 | |
15 | |
25 | |
30 |
Question 1 Explanation:
Step-1: Given number of equivalence classes with 5 elements with three elements in each class will be 1,2,2 (or) 2,1,2 (or) 2,2,1 and 3,1,1.
Step-2: The number of combinations for three equivalence classes are
2,2,1 chosen in ( 5 C 2 * 3 C 2 * 1 C 1 )/2! = 15
3,1,1 chosen in( 5 C 2 * 3 C 2 * 1 C 1 )/2! = 10
Step-3: Total differential classes are 15+10
=25.
Step-2: The number of combinations for three equivalence classes are
2,2,1 chosen in ( 5 C 2 * 3 C 2 * 1 C 1 )/2! = 15
3,1,1 chosen in( 5 C 2 * 3 C 2 * 1 C 1 )/2! = 10
Step-3: Total differential classes are 15+10
=25.
Question 2 |
The number of different spanning trees in complete graph, K 4 and bipartite graph, K 2,2 have ______ and _______ respectively.
14, 14 | |
16, 14 | |
16, 4 | |
14, 4 |
Question 2 Explanation:
Step-1: Given complete graph K 4 .To find total number of spanning tree in complete graph using standard formula is n (n-2)
Here, n=4
=n (n-2)
= 4 2
=16
Step-2: Given Bipartite graph K 2,2 . To find number of spanning tree in a bipartite graph K m,n having standard formula is m (n-1) * n (m-1) .
m=2 and n=2
= 2 (2-1) * 2 (2-1)
= 2 * 2
= 4
=n (n-2)
= 4 2
=16
Step-2: Given Bipartite graph K 2,2 . To find number of spanning tree in a bipartite graph K m,n having standard formula is m (n-1) * n (m-1) .
m=2 and n=2
= 2 (2-1) * 2 (2-1)
= 2 * 2
= 4
Question 3 |
Suppose that R 1 and R 2 are reflexive relations on a set A.
Which of the following statements is correct ?
R 1 ∩ R 2 is reflexive and R 1 ∪ R 2 is irreflexive. | |
R 1 ∩ R 2 is irreflexive and R 1 ∪ R 2 is reflexive. | |
Both R 1 ∩ R 2 and R 1 ∪ R 2 are reflexive. | |
Both R 1 ∩ R 2 and R 1 ∪ R 2 are irreflexive. |
Question 3 Explanation:
A binary relation R over a set X is reflexive if every element of X is related to itself. Formally, this may be written ∀ x ∈X : xRx.
Ex: Let set A={0,1}
R 1 ={(0,0),(1,1)} all diagonal elements we are considering for reflexive relation.
R 2 ={(0,0),(1,1)} all diagonal elements we are considering for reflexive relation.
R 1 ∩ R 2 must have {(0,0),(1,1)} is reflexive.
R 1 ∪ R 2 must have {(0,0),(1,1)} is reflexive.
Ex: Let set A={0,1}
R 1 ={(0,0),(1,1)} all diagonal elements we are considering for reflexive relation.
R 2 ={(0,0),(1,1)} all diagonal elements we are considering for reflexive relation.
R 1 ∩ R 2 must have {(0,0),(1,1)} is reflexive.
R 1 ∪ R 2 must have {(0,0),(1,1)} is reflexive.
Question 4 |
There are three cards in a box. Both sides of one card are black, both sides of one card are red, and the third card has one black side and one red side. We pick a card at random and observe only one side.
What is the probability that the opposite side is the same colour as the one side we observed?
3/4 | |
2/3 | |
1/2 | |
1⁄3 |
Question 4 Explanation:
Given data,
-- 3 cards in a box
-- 1 st card: Both sides of one card is black. The card having 2 sides. We can write it as BB.
-- 2 nd card: Both sides of one card is red. The card having 2 sides. We can write it as RR.
-- 3rd card: one black side and one red side. We can write it as BR.
Step-1: The probability that the opposite side is the same colour as the one side we observed is 2⁄3 because total number of cards are 3
-- 3 cards in a box
-- 1 st card: Both sides of one card is black. The card having 2 sides. We can write it as BB.
-- 2 nd card: Both sides of one card is red. The card having 2 sides. We can write it as RR.
-- 3rd card: one black side and one red side. We can write it as BR.
Step-1: The probability that the opposite side is the same colour as the one side we observed is 2⁄3 because total number of cards are 3
Question 5 |
A clique in a simple undirected graph is a complete subgraph that is not contained in any larger complete subgraph. How many cliques are there in the graph shown below?
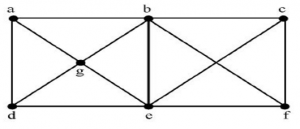

2 | |
4 | |
5 | |
6 |
Question 5 Explanation:
Definition of clique is already given in question.
Definition: A clique in a simple undirected graph is a complete subgraph that is not contained in any larger complete subgraph.
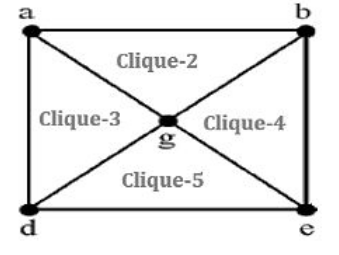
Step-1: b,c,e,f is complete graph.
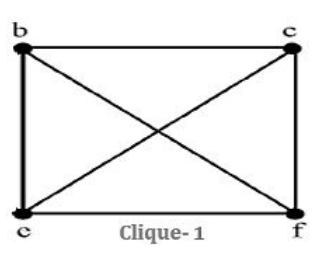
Step-2: ‘a’ is not connected to ‘e’ and ‘b’ is not connected to ‘d’. So, it is not complete graph.
Definition: A clique in a simple undirected graph is a complete subgraph that is not contained in any larger complete subgraph.
Step-1: b,c,e,f is complete graph.

Step-2: ‘a’ is not connected to ‘e’ and ‘b’ is not connected to ‘d’. So, it is not complete graph.

Question 6 |
Which of the following logic expressions is incorrect?
1 ⊕ 0 = 1 | |
1 ⊕ 1 ⊕ 1 = 1 | |
1 ⊕ 1 ⊕ 0 = 1 | |
1 ⊕ 1 = 0 |
Question 6 Explanation:
Here, ⊕ is nothing but Ex-OR operator. The truth table for Ex-OR is
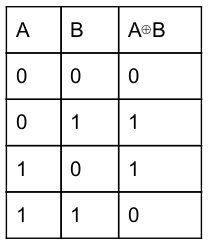
According to truth table,
Option-A is TRUE
Option-B is a 1 ⊕ 1 is 0.
0 ⊕ 1 is 1(TRUE)
Option-C is 1 ⊕ 1 is 0.
0 ⊕ 0 = 0 but given 1. So, FALSE
Option-D is TRUE.

According to truth table,
Option-A is TRUE
Option-B is a 1 ⊕ 1 is 0.
0 ⊕ 1 is 1(TRUE)
Option-C is 1 ⊕ 1 is 0.
0 ⊕ 0 = 0 but given 1. So, FALSE
Option-D is TRUE.
Question 7 |
The IEEE-754 double-precision format to represent floating point numbers, has a length of _____ bits.
16 | |
32 | |
48 | |
64 |
Question 7 Explanation:
→ The IEEE-754 double-precision format to represent floating point numbers has a length of 64 bits
→ In the IEEE 754-2008 standard, the 64-bit base-2 format is officially referred to as binary64 called double in IEEE 754-1985.
→ IEEE 754 specifies additional floating-point formats, including 32-bit base-2 single precision and, more recently, base-10 representations.
→ In the IEEE 754-2008 standard, the 64-bit base-2 format is officially referred to as binary64 called double in IEEE 754-1985.
→ IEEE 754 specifies additional floating-point formats, including 32-bit base-2 single precision and, more recently, base-10 representations.
Question 8 |
Simplified Boolean equation for the following truth table is:
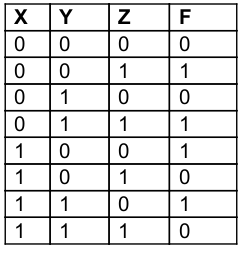

F = yz’ + y’z | |
F = xy’ + x’y | |
F = x’z + xz’ | |
F = x’z + xz’ + xyz |
Question 8 Explanation:
Method-1: Using K-Map
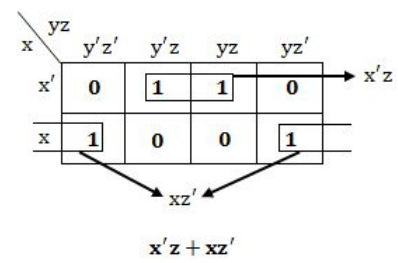
Method-2: Using boolean simplification
= x’y’z+x’yz+xy’z’+xyz’
= x'z(y'+y)+ xz'(y'+y)
= x'z+xz' (Since y'+y=1)

Method-2: Using boolean simplification
= x’y’z+x’yz+xy’z’+xyz’
= x'z(y'+y)+ xz'(y'+y)
= x'z+xz' (Since y'+y=1)
Question 9 |
The simplified form of a Boolean equation (AB’ + AB’C + AC) (A’C’ + B’) is :
AB’ | |
AB’C | |
A’B | |
ABC |
Question 9 Explanation:
(AB’ + AB’C + AC) (A’C’ + B’)
= (AB'+AC) (A'C'+B')
= AB'A'C' + AB'B' + ACA'C' + ACB'
= AB'B' + ACB'
= AB'(C+1)
= AB'
= (AB'+AC) (A'C'+B')
= AB'A'C' + AB'B' + ACA'C' + ACB'
= AB'B' + ACB'
= AB'(C+1)
= AB'
Question 10 |
In a positive-edge-triggered JK flip-flop, if J and K both are high then the output will be _____ on the rising edge of the clock.
No change | |
Set | |
Reset | |
Toggle |
Question 10 Explanation:
Positive-edge-triggered JK flip-flop is
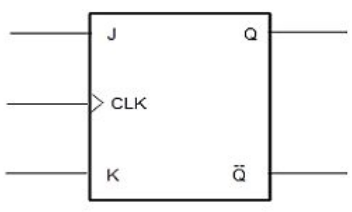
The Truth Table for the JK Function

When J = 1 and K = 1 , The output continuously Toggles from 1 to 0 and 0 to 1. At the end Output is indeterminate. This condition is called as Race around Condition. This happens when Propagation Delay is less than the Pulse width.

The Truth Table for the JK Function

When J = 1 and K = 1 , The output continuously Toggles from 1 to 0 and 0 to 1. At the end Output is indeterminate. This condition is called as Race around Condition. This happens when Propagation Delay is less than the Pulse width.
Question 11 |
Given i = 0, j = 1, k = –1 x = 0.5, y = 0.0 What is the output of the following expression in C language ?
x * y < i + j || k
x * y < i + j || k
-1 | |
0 | |
1 | |
2 |
Question 11 Explanation:
x * y < i + j || k
Step-1: Evaluate x * y because multiplication has more priority than remaining operators
x * y→ 0
Step-2: i + j is 1
Step-3: (x*y) < (i+j) is 1. Because relational operators only return 1(TRUE) or 0(FALSE).
Step-4: ((x*y) < (i+j)) || k is logical OR operator.
1 || -1 will returns 1.
Note: The precedence is ((x*y) < (i+j)) || k
Step-1: Evaluate x * y because multiplication has more priority than remaining operators
x * y→ 0
Step-2: i + j is 1
Step-3: (x*y) < (i+j) is 1. Because relational operators only return 1(TRUE) or 0(FALSE).
Step-4: ((x*y) < (i+j)) || k is logical OR operator.
1 || -1 will returns 1.
Note: The precedence is ((x*y) < (i+j)) || k
Question 12 |
The following statement in ‘C’
int (*f())[ ];
declares
int (*f())[ ];
declares
a function returning a pointer to an array of integers. | |
a function returning an array of pointers to integers. | |
array of functions returning pointers to integers. | |
an illegal statement. |
Question 12 Explanation:
int (*f())[ ] declare a function returning a pointer to an array of integers.
There are 12 questions to complete.
