GATE 2016 [Set-1]
Question 1 |
Out of the following four sentences, select the most suitable sentence with respect to grammar and usage.
I will not leave the place until the minister does not meet me. | |
I will not leave the place until the minister doesn’t meet me. | |
I will not leave the place until the minister meet me. | |
I will not leave the place until the minister meets me. |
Minister is a singular person, with a singular object, so verb ends with 's'. So option C is incorrect.
Option 'D' is correct.
Question 2 |
A rewording of something written or spoken is a ______________.
paraphrase | |
paradox | |
paradigm | |
paraffin |
Question 3 |
Archimedes said, “Give me a lever long enough and a fulcrum on which to place it, and I will move the world.”
The sentence above is an example of a ___________ statement.
figurative | |
collateral | |
literal | |
figurine |
The use of the metaphorical words to explain about the thoughts instead of literal use of them.
Question 4 |
If ‘relftaga’ means carefree, ‘otaga’ means careful and ‘fertaga’ means careless, which of the following could mean ‘aftercare’?
zentaga | |
tagafer | |
tagazen | |
relffer |
otaga - careful → (2)
fertaga - careless → (3)
From (1) & (2),
taga = care (and it is in the first half of the word)
From (3),
fer = less
Aftercare - tagazen
Care is in the second half of the word ⇒ taga should be in the first half.
Question 5 |
A cube is built using 64 cubic blocks of side one unit. After it is built, one cubic block is removed from every corner of the cube. The resulting surface area of the body (in square units) after the removal is __________.
56 | |
64 | |
72 | |
96 |
⇒ Side of cube = 4
Surface area of cube = 6s2 = 6 × 42 = 96
Each corner block is associated with three faces of cube.
When they are removed, three new faces are exposed. Thus there appears no net change in the exposed surface area.
Hence, Surface area = 96
Question 6 |
A shaving set company sells 4 different types of razors, Elegance, Smooth, Soft and Executive. Elegance sells at Rs. 48, Smooth at Rs. 63, Soft at Rs. 78 and Executive at Rs. 173 per piece. The table below shows the numbers of each razor sold in each quarter of a year.

Which product contributes the greatest fraction to the revenue of the company in that year?
Elegance | |
Executive | |
Smooth | |
Soft |
Revenue from Smooth = (20009 + 19392 + 22429 + 18229) × 63 = Rs. 5043717
Revenue from Soft = (17602 + 18445 + 19544 + 16595) × 78 = Rs.5630508
Revenue from Executive = (9999 + 8942 + 10234 + 10109) × 173 = Rs. 6796132
Clearly, Executive contributes the greatest fraction to the revenue of the company as the revenue from it is the highest.
Question 7 |
Indian currency notes show the denomination indicated in at least seventeen languages. If this is not an indication of the nation’s diversity, nothing else is.
Which of the following can be logically inferred from the above sentences?
India is a country of exactly seventeen languages. | |
Linguistic pluralism is the only indicator of a nation’s diversity. | |
Linguistic pluralism is the only indicator of a nation’s diversity. | |
Linguistic pluralism is strong evidence of India’s diversity. |
Which is inferred from the statement.
Option A, B, C are incorrect which are not properly inferred from the statement.
Question 8 |
Consider the following statements relating to the level of poker play of four players P, Q, R and S.
-
I. P always beats Q
II. R always beats S
III. S loses to P only sometimes
IV. R always loses to Q
Which of the following can be logically inferred from the above statements?
-
(i) P is likely to beat all the three other players
(ii) S is the absolute worst player in the set
(i) only | |
(ii) only | |
(i) and (ii) | |
neither (i) nor (ii) |
All three can beat S.
But from statement III,
S loses to P only sometimes.
(ii) Cannot be inferred.
And in poker, the transitive law does not apply. This can be seen from statement III.
As S loses to P only sometimes which states that wins against P most of the time.
So, (i) cannot be logically inferred.
Question 9 |
If f(x) = 2x7 + 3x - 5, which of the following is a factor of f(x)?
(x 3 +8) | |
(x-1) | |
(2x-5) | |
(x+1) |
For (x - a) to be a factor of f(x)
f(a) = 0
From options,
Only a=1, satisfies the above equation
∴ (x - 1) is a factor of f(x).
Question 10 |
In a process, the number of cycles to failure decreases exponentially with an increase in load. At a load of 80 units, it takes 100 cycles for failure. When the load is halved, it takes 10000 cycles for failure. The load for which the failure will happen in 5000 cycles is ________.
40.00 | |
46.02 | |
60.01 | |
92.02 |
General exponential function = a⋅e-bx
i.e., No. of cycles to failure = a⋅e-bx
load = x
At a load of 80 units, it takes 100 cycles to failure.
So, no. of cycles to failure = 100
load = 80
i.e., 100 = a⋅e - b(80) --------(1)
When the load is halved, it takes 10000 cycles to failure.
No. of cycles to failure = 10,000
load = 40
i.e., 10,000 = a⋅e - b(40) ---------(2)
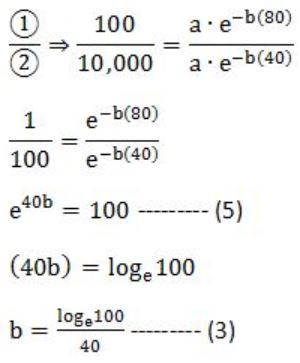
No. of cycles to failure = 5,000
load = x?
i.e., 5000 = a⋅e - bx
Multiply with 2 on both sides,
10,000 = 2⋅a⋅e - bx ------- (4)
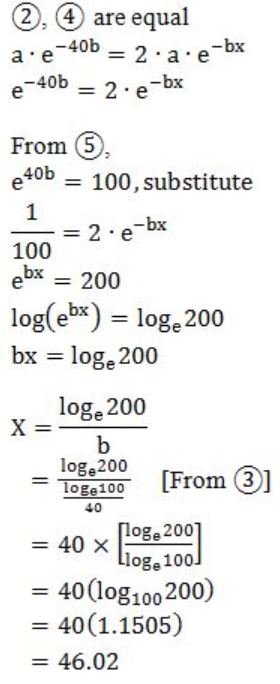
Question 11 |
p: x ∈ {8,9,10,11,12}
q: x is a composite number
r: x is a perfect square<
s: x is a prime number
The integer x≥2 which satisfies ¬((p ⇒ q) ∧ (¬r ∨ ¬s)) is _________.
11 | |
12 | |
13 | |
14 |
~((p→q) ∧ (~r ∨ ~S))
⇒ first simplify the given statement by converging them to ∧, ∨
⇒ [~(p→q) ∨ (~(~r ∨ ~s)]
Demorgan’s law:
⇒ [~(~p ∨ q) ∨ (r ∧ s)]
∵ p→q ≡ ~p ∨ q
⇒ [(p ∧ ~q) ∨ (r ∧ s)]
p ∧ ~q is {8,9,10,11,12} ∧ {not a composite number} i.e. {11}
r ∧ s is {perfect square} ∧ {prime} i.e. no answer
So, the one and only answer is 11.
Question 12 |
Let an be the number of n-bit strings that do NOT contain two consecutive 1s. Which one of the following is the recurrence relation for an?
an = a(n-1) + 2a(n-2) | |
an = a(n-1) + a(n-2) | |
an = 2a(n-1) + a(n-2) | |
an = 2a(n-1) + 2a(n-2) |
If n=1, we have {0,1}
# Occurrences = 2
If n=2, we have {00,01,10}
# Occurrences = 3
If n=3, we have {000,001,010,100,101}
# Occurrences = 5
It is evident that a3 = a1 + a2
Similarly, an = an-1 + an-2
Question 13 |
4 | |
3 | |
2 | |
1 |
Question 14 |
A probability density function on the interval [a,1] is given by 1/x2 and outside this interval the value of the function is zero. The value of a is _________.
0.7 | |
0.6 | |
0.5 | |
0.8 |
or
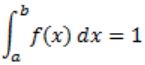
where (a, b) is internal and f(x) is probability density function.
Given,
f(x) = 1/x2 , a≤x≤1
The area under curve,
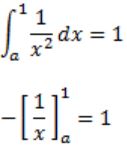
- 1 + 1/a = 1
1/a = 2
a = 0.5
Question 15 |
Two eigenvalues of a 3 × 3 real matrix P are (2 + √-1) and 3. The determinant of P is __________.
18 | |
15 | |
17 | |
16 |
So, For the given 3×3 matrix there would be 3 eigen values.
Given eigen values are : 2+i and 3.
So the third eigen value should be 2-i.
As per the theorems, the determinant of the matrix is the product of the eigen values.
So the determinant is (2+i)*(2-i)*3 = 15.
Question 16 |
Consider the Boolean operator with the following properties:
Then x#y is equivalent to
 | |
 | |
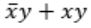 | |
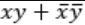 |
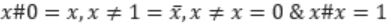
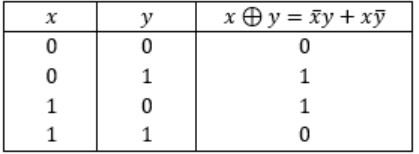
Ex-OR satisfies all the properties. Hence,
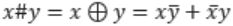
![GATE 2016 [Set-1]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)