GATE 2019
Question 1 |
Ten friends planned to share equally the cost of buying a gift for their teacher. When two of them decided not to contribute, each of the other friends had to pay Rs 150 more. The cost of the gift was Rs. _____.
12000 | |
666 | |
3000 | |
6000 |
Gift cost = 10x
When two people are not going to contribute then remaining friends have to pay Rs 150 more.
Two friends contribution = 150 × 8 = 1200
One friend contribution = 600
Ten friends contribution = 6000
Cost of the Gift = 6000
Method-2: There were ten friends decided to buy a gift.
Out of ten members two members are not able to pay their share.
So, two members amount was paid by remaining eight members.
Then the eight members has to pay 150 more, which is 150*8= 1200( two persons share).
One person share= 1200/2=600.
Ten members share= 600*10= 6000.
Price of the gift= 6000.
Question 2 |
The expenditure on the project _____ as follows; equipment Rs.20 lakhs, salaries Rs.12 lakhs, and contingency Rs.3 lakhs.
break down | |
break | |
breaks down | |
breaks |
Question 3 |
The search engine's business model _____ around the fulcrum of trust.
bursts | |
revolves | |
sinks | |
plays |
Question 4 |
Two cars start at the same time from the same location and go in the same direction. The speed of the first car is 50 Km/h and the speed of the second car is 60 Km/h. The number of hours it takes for the distance between the two cars to be 20 Km is _____.
2 | |
3 | |
1 | |
6 |
Speed of the second car = 60 km/h
Let no. of hours = x say
⇒ From the question we can write
(60)x - (50)x = 20
10x = 20
∴ x = 2 hrs
Question 5 |
A court is to a judge as _____ is to a teacher.
a syllabus | |
a student | |
a punishment | |
a school |
Question 6 |
In a college, there are three student clubs. Sixty students are only in the Drama club, 80 students are only in the Dance club, 30 students are only in the Maths club, 40 students are in both Drama and Dance clubs, 12 students are in both Dance and Maths clubs, 7 students are in both Drama and Maths club, and 2 students are in all the clubs. If 75% of the students in the college are not in any of these clubs, then the total number of students in the college is _____.
900 | |
975 | |
225 | |
1000 |
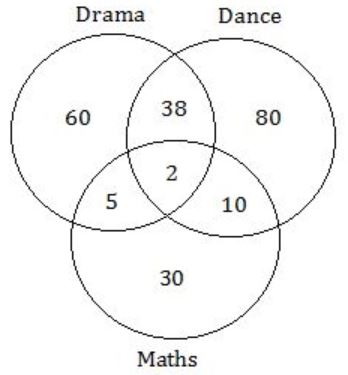
No. of students present in three student clubs
= 60 + 80 + 30 + 38 + 2 + 10 + 5
= 225 [i.e., 25% of the students in the college]
Total no. of students in the college = 225 × 4 = 900
Question 7 |
The police arrested four criminals - P, Q, R and S. The criminals knew each other. They made the following statements:
-
P says "Q committed the crime."
Q says "S committed the crime."
R says "I did not do it."
S says "What Q said about me is false."
Assume only one of the arrested four committed the crime and only one of the statements made above is true. Who committed the crime?
P | |
Q | |
R | |
S |
II, III, IV are false.
II is false: 'S' is not criminal.
IV is also false: 'S' committed crime.
There is conflict among I, IV now as P, S both should be criminals.
⇒ II true: 'S' is criminal.
I, III, IV are false.
IV is false. So, 'S' is not criminal.
III is false. So. 'R' is criminal.
There is conflict among II, III as S, R both should be criminal.
III is true: Criminal ≠ R.
I, II, IV are false.
I is false. So, 'Q' is also not criminal.
II is false. So, 'S' is not criminal.
IV is false. So, 'S' is not criminal.
Q, R, S are not criminals. So, 'P' is criminal.
IV is true: I, II, III are false.
II is false. So, 'S' is not criminal.
IV is true. So, 'S' is criminal.
I is false. So, 'Q' is not criminal.
III is false. So, 'R' is criminal.
There is conflict, as R, S both should be criminals.
Question 8 |
"A recent High Court judgement has sought to dispel the idea of begging as a disease — which leads to its stigmatization and criminalization — and to regard it as a symptom. The underlying disease is the failure of the state to protect citizens who fall through the social security net."
Which of the following statements can be inferred from the given passage?
Beggars are created because of the lack of social welfare schemes | |
Beggars are lazy people who beg because they are unwilling to work | |
Begging is an offence that has to be dealt with firmly | |
Begging has to be banned because it adversely affects the welfare of the state |
The court is judged that because of failure of the state to protect citizens through social security schemes beggars are created.
Question 9 |
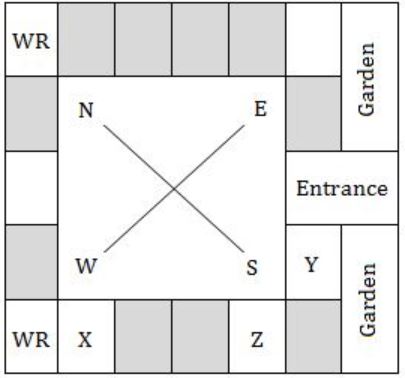
Three of the five students allocated to a hostel put in special requests to the warden. Given the floor plan of the vacant rooms, select the allocation plan that will accommodate all their requests.
-
Request by X: Due to pollen allergy, I want to avoid a wing next to the garden.
Request by Y: I want to live as far from the washrooms as possible, since I am very sensitive to smell.
Request by Z: I believe in Vaastu and so want to stay in the South-west wing.
The shaded rooms are already occupied. WR is washroom.
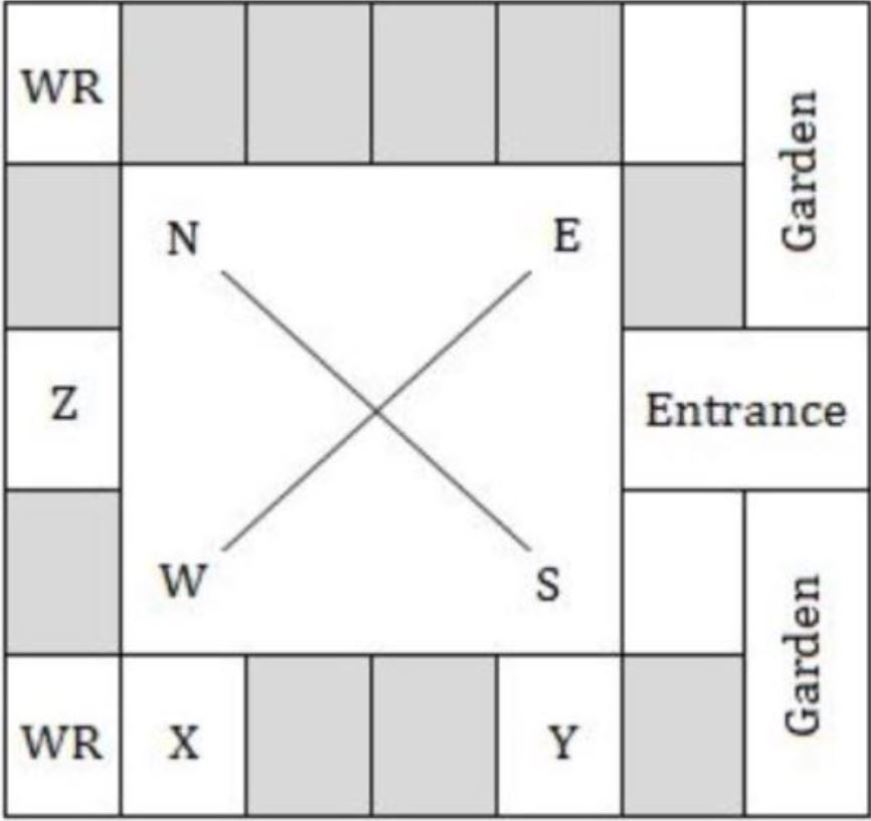 | |
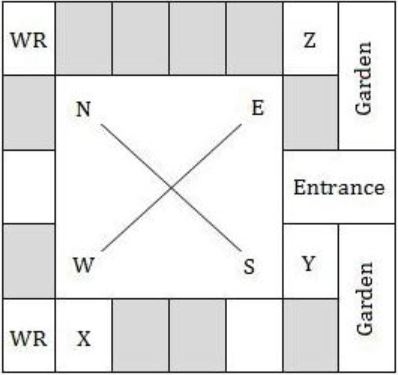 | |
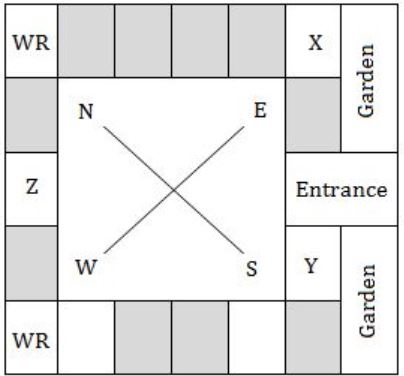 | |
 |
Question 10 |
In the given diagram, teachers are represented in the triangle, researchers in the circle and administrators in the rectangle. Out of the total number of the people, the percentage of administrators shall be in the range of _____.

16 to 30 | |
0 to 15 | |
46 to 60 | |
31 to 45 |
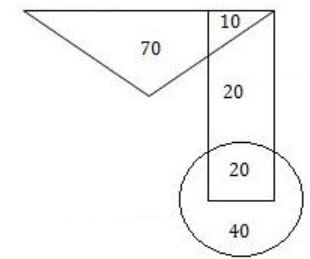
From the given diagram:
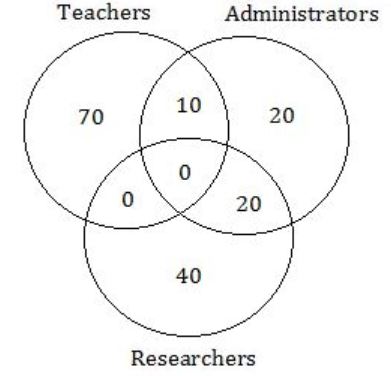
Total no. of people = 70 + 10 + 20 + 20 + 40 = 160
No. of Administrators = 50
% of Administrators = 50/160 = 31.25
Question 11 |
If L is a regular language over Σ = {a,b}, which one of the following languages is NOT regular?
Suffix (L) = {y ∈ Σ* such that xy ∈ L} | |
{wwR │w ∈ L} | |
Prefix (L) = {x ∈ Σ*│∃y ∈ Σ* such that xy ∈ L} | |
L ∙ LR = {xy │ x ∈ L, yR ∈ L} |
Question 12 |
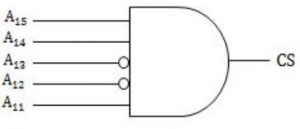
The chip select logic for a certain DRAM chip in a memory system design is shown below. Assume that the memory system has 16 address lines denoted by A15 to A0. What is the range of addresses (in hexadecimal) of the memory system that can get enabled by the chip select (CS) signal?
C800 to C8FF | |
C800 to CFFF | |
DA00 to DFFF | |
CA00 to CAFF |
The chip select address for given figure:
A4 - A15 = 25
So, total addressable loactions = 216/25 = 211
211 = 2048 or location 0 to 2047
∴ CFFF - C800 = 2047
Answer is C800 to CFFF.
Question 13 |
1 | |
Limit does not exist | |
53/12 | |
108/7 |
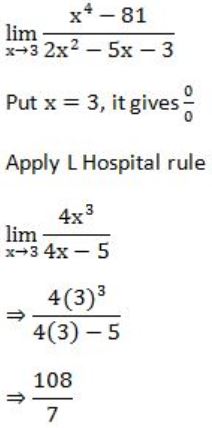
Question 14 |
Which of the following protocol pairs can be used to send and retrieve e-mails (in that order)?
SMTP, MIME | |
SMTP, POP3 | |
IMAP, POP3 | |
IMAP, SMTP |
POP3: Post Office Protocol (Responsible for retrieve email)
SMTP: Simple Mail Transfer Protocol (Responsible for send Email)
IMAP: Internet Message Access protocol (Responsible for store and view)
MIME: Multi purpose Internet Mail Extensions (For media)
Question 15 |
Which one of the following statements is NOT correct about the B+ tree data structure used for creating an index of a relational database table?
Each leaf node has a pointer to the next leaf node | |
Non-leaf nodes have pointers to data records | |
B+ Tree is a height-balanced tree | |
Key values in each node are kept in sorted order |
In B+ trees non-leaf nodes do not have pointers to data records.
Question 16 |
Consider the following C program:
#include <stdio.h>
int main () {
int arr [] = {1,2,3,4,5,6,7,8,9,0,1,2,5}, *ip = arr+4;
printf ("%d\n", ip[1]);
return 0;
}
The number that will be displayed on execution of the program is _____.
5 | |
6 | |
7 | |
8 |
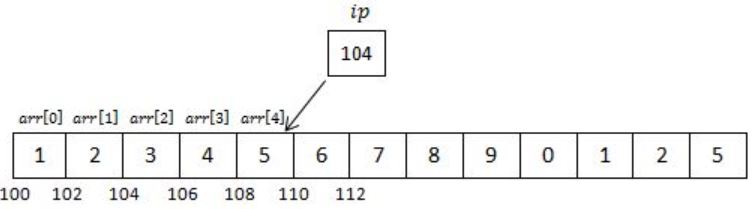
We know that arr is a pointer to arr[ ] & hence arr+4 is pointer to 4th index of array (starting from 0 to 4).
Now *ip is a pointer of int type pointing to memory location 108, which is part of arr.
Hence, when we will print ip[1] it will be equivalent to *(ip+1).
Address of ip will be incremented by 1 & value inside 110 will be printed.
