Computer-Organization
Question 1 |

Assume that the content of the memory location 5000 is 10, and the content of the register R3 is 3000. The content of each of the memory locations from 3000 to 3010 is 50. The instruction sequence starts from the memory location 1000. All the numbers are in decimal format. Assume that the memory is byte addressable.
After the execution of the program, the content of memory location 3010 is _______
A | 50 |
Register R1 will get value 10 from location 5000. So the loop in the given program will run for 10 times as the loop condition is based on ‘Dec R1’. When R1 is 0 then the loop terminates.
In these 10 iterations of the loop contents of memory locations 3000 to 3009 are changed as initial value of R3 is 3000 and in each iteration we update M[R3] ← R2 and the value of R3 is incremented to the next location 3001, 3002 etc.
But the value in location 3010 is unchanged and it will be the same as the initial value which is 50.
Question 2 |
A | 17160 |
In a pipeline with k-stages, number of cycles to execute n instructions = (k+n-1) cycles
Here k = 5, n = 100
So we need a total of 5+100-1 = 104 cycles.
Clock cycle time = maximum of all stage delays + register delay
= max(150, 120, 150, 160, 140) + 5 = 160+5 = 165 ns
Time in ns = 104*165 = 17160ns
Question 3 |
A | 17 |
Given that the main memory is 2^32 bytes. So the physical address is 32 bits long.
Since it is a direct mapped cache the physical address is divided into fields as (TAG, LINE, OFFSET).
Cache size is 32KB = 2^15 Bytes.
Block size is 64 bytes = 2^6 bytes, so OFFSET needs 6 bits.
Number of blocks in the cache = 2^15//2^6 = 2^9, So LINE number needs 9 bits.
TAG bits = 32 - 9 - 6 = 17 bits.
Question 4 |
Which of the following is (are) valid FORTRAN 77 statement(s)?
A | DO 13 I = 1 |
B | A = DIM ***7 |
C | READ = 15.0 |
D | GO TO 3 = 10 |
Question 5 |
Assume that each character code consists of 8 bits. The number of characters that can be transmitted per second through an asynchronous serial line at 2400 baud rate, and with two stop bits, is
A | 109 |
B | 216 |
C | 218 |
D | 219 |
= 8 bit data + 2 stop bit + 1 start bit
= 11 bits
No. of characters = 2400/11 = 218.18
Since, it is asked for transmitted characters we take floor and answer is 218.
Question 6 |
The details of an interrupt cycle are shown in figure.
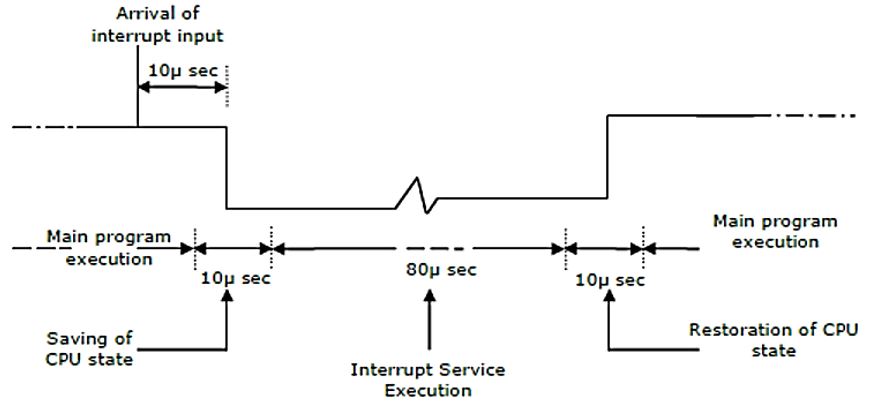
Given that an interrupt input arrives every 1 msec, what is the percentage of the total time that the CPU devotes for the main program execution.
A | 90% |
= saving state of CPU + ISR execution + restoring of CPU state
= (80 + 10 + 10) × 10-6
= 100 μs
For every 1ms an interrupt occurs which is served for 100 μs.
1ms = 1000μs
Thus, for every 1000μs, (1000 - 100) = 900 μs of main program and 100μs of interrupt overhead exists.
Thus, 900/1000 is usage of CPU to execute main program .
∴ % of CPU to execute main program is (900/1000) × 100 = 90%
Question 7 |
A simple two-pass assembler does the following in the first pass:
A | It allocates space for the literals. |
B | It computes the total length of the program |
C | It builds the symbol table for the symbols and their values. |
D | It generates code for all the load and store register instructions. |
E | A, B and C |
1) Assign address to all statements in the program.
2) Save the values assigned to all tables for use in pass 2.
3) Perform some processing of assembler directives.
Question 8 |
The instruction format of a CPU is:
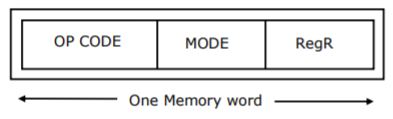
Mode and RegR together specify the operand. RegR specifies a CPU register and Mode specifies an addressing mode. In particular, Mode = 2 specifies that ‘the register RegR contains the address of the operand, after fetching the operand, the contents of RegR are incremented by 1’.
An instruction at memory location 2000 specifies Mode = 2 and the RegR refers to program counter (PC).
(a) What is the address of the operand?
(b) Assuming that this is a non-jump instruction, what are the contents of PC after the execution of this instruction?
A | Theory Explanation. |
Question 9 |
In the three-level memory hierarchy shown in the following table, pi denotes the probability that an access request will refer to Mi.

If a miss occurs at level Mi, a page transfer occurs from Mi+1 to Mi and the average time required for such a page swap is Ti. Calculate the average time tA required for a processor to read one word from this memory system.
A | Theory Explanation. |
Question 10 |
An ISAM (indexed sequential) file consists of records of size 64 bytes each, including key field of size 14 bytes. An address of a disk block takes 2 bytes. If the disk block size is 512 bytes and there are 16 K records, compute the size of the data and index areas in terms of number of blocks. How many levels of tree do you have for the index?
A | Theory Explanation. |
Question 11 |
Given that the following is an 8085 program segment:
(a) Identify the function performed by it, and
(b) List the roles of the registers used and the address referred to by it.
LHLD 5000
MVI B, 5
GET: IN 20
MOV M, A
INX H
DCR B
JNZ GET A | Theory Explanation. |
Question 12 |
Which one of the following statements is true?
A | Macro definitions cannot appear within other macro definitions in assembly language programs |
B | Overlaying is used to run a program which is longer than the address space of computer |
C | Virtual memory can be used to accommodate a program which is longer than the address space of a computer |
D | It is not possible to write interrupt service routines in a high level language |
Question 13 |
State True or False with one line explanation
Multiplexing of address/data lines in 8085 microprocessor reduces the instruction
execution time.
A | True |
B | False |
The major reason of multiplexing address and data bus is to reduce the number of pins for address and data and dedicate those pins for other several functions of micro-processor.
Question 14 |
State True or False with one line explanation
Expanding opcode instruction formats are commonly employed in RISC. (Reduced Instruction Set Computers) machines.
A | True |
B | False |
Now the challenge is: How to fit multiple sets of instructions types into limited or fixed size instruction format.
Here comes expanding opcode into the picture, So RISC system uses expanding opcode technique to have fixed size instructions.
Question 15 |
State True or False with one line explanation
A FSM (Finite State Machine) can be designed to add two integers of any arbitrary length (arbitrary number of digits).
A | True |
B | False |
→ q0: Start state to represent carry bit is 0.
→ q1: State to represent carry bit is 1.
The inputs to the FA will be pairs of bits, i.e., 00, 01, 10, 11.
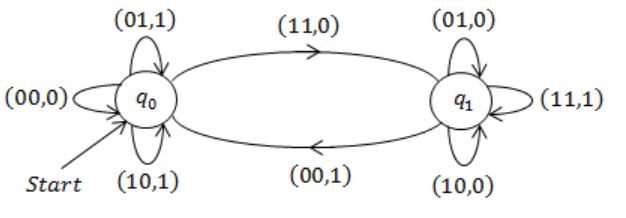
The FA starts in state 1 (since carry is 0) and inputs a pair of bits. If the pair is 11, the FA outputs a '0' and switches to state 2 (since the carry is 1), where the next pair of bits is input and is added to a carry bit of 1.
Question 16 |
Match the following items

A | (i) - (a), (ii) - (b), (iii) - (d), (iv) - (c) |
Question 17 |
State whether the following statements are True or False with reasons for your answer:
(a) Coroutine is just another name for a subroutine.
(b) A two pass assembler uses its machine opcode table in the first pass of assembly.
A | Theory Explanation. |
Question 18 |
State whether the following statements are True or False with reasons for your answer
(a) A subroutine cannot always be used to replace a macro in an assembly language program.
(b) A symbol declared as ‘external’ in assembly language is assigned an address outside the program by the assembler itself.
A | Theory Explanation. |
Question 19 |
A single instruction to clear the lower four bits of the accumulator in 8085 assembly language?
A | XRI OFH |
B | ANI FOH |
C | XRI FOH |
D | ANI OFH |
→ The XOR's don't reliably clear random bits and ANI OF clears the upper nibble, not the lower nibble.
Question 20 |
In a vectored interrupt
A | the branch address is assigned to a fixed location in memory |
B | the interrupt source supplies the branch information to the processor through an interrupt vector |
C | the branch address is obtained from a register in the processor |
D | none of the above |
Question 21 |
The principle of locality justifies the use of
A | interrupts |
B | DMA |
C | Polling |
D | Cache Memory |
→ The things which are used more frequently those are stored in locality of reference.
→ For this purpose we use the cache memory.
Question 22 |
What are x and y in the following macro definition?
macro Add x,y Load y Mul x Store y end macro
A | Variables |
B | Identifiers |
C | Actual parameters |
D | Formal parameters |
Question 23 |
The capacity of a memory unit is defined by the number of words multiplied by the number of bits/word. How many separate address and data lines are needed for a memory of 4K × 16?
A | 10 address, 16 data lines |
B | 11 address, 8 data lines |
C | 12 address, 16 data lines |
D | 12 address, 12 data lines |
m = no. of address lines
n = no. of data lines
Given, 4K × 16 = 212 × 16
Address lines = 12
Data lines = 16
Question 24 |
A computer system has a 4K word cache organized in block-set-associative manner with 4 blocks per set, 64 words per block. The number of its in the SET and WORD fields of the main memory address format is:
A | 15, 40 |
B | 6, 4 |
C | 7, 2 |
D | 4, 6 |
So we need 4 set bits.
And,
64 words per block means WORD bit is 6-bits.
So, answer is option (D).
Question 25 |
If the overhead for formatting a disk is 96 bytes for 4000 byte sector,
(a) Compute the unformatted capacity of the disk for the following parameters:
Number of surfaces: 8 Outer diameter of the disk: 12 cm Inner diameter of the disk: 4 cm Inter track space: 0.1 mm Number of sectors per track: 20
(b) if the disk in (a) is rotating at 360 rpm, determine the effective data transfer rate which is defined as the number of bytes transferred per second between disk and memory.
A | Theory Explanation. |
Question 26 |
The following is an 8085 assembly language program:
MVI B, OAH
MVI A, 05H
LXI H, IC40H
CALL SUB
HLT
SUB CMP M
RZ
INX H
DCR B
JNZ SUB
RET
(a) What does the program do?
(b) What are the contents of registers A and B initially?
(c) What are the contents of HL register pair after the execution of the program?
A | Theory Explanation. |
Question 27 |
A sequence of two instructions that multiplies the contents of the DE register pair by 2 and stores the result in the HL register pair (in 8085 assembly language) is:
A | XCHG and DAD B |
B | XTHL and DAD H |
C | PCHL and DAD D |
D | XCHG and DAD H |
Question 28 |
Consider the following statements.
- I. Daisy chaining is used to assign priorities in attending interrupts.
II. When a device raises a vectored interrupt, the CPU does polling to identify the source of the interrupt.
III. In polling, the CPU periodically checks the status bits to know if any device needs its attention.
IV. During DMA, both the CPU and DMA controller can be bus masters at the same time.
Which of the above statements is/are TRUE?
A | I and IV only |
B | I and II only
|
C | III only |
D | I and III only
|
Statement-II is false as vectored interrupt doesn’t involve polling but non-vectored interrupt involves polling.
Statement-III is true as polling means that CPU periodically checks the status bits to know if any device needs attention.
Statement-IV is false as during DMA only one of the CPU or DMA can be bus master at a time.
Question 29 |
A direct mapped cache memory of 1 MB has a block ize of 256 bytes. The cache has an access time of 3 ns and a hit rate of 94%. During a cache miss, it takes 20 ns to bring the first word of a block from the main memory, while each subsequent word takes 5 ns. The word size is 64 bits. The average memory access time in ns (round off to 1 decimal place) is _____.
A | 13.5 |
Hit ratio of cache = 0.94
Word size is 64 bits = 8 bytes.
Cache line size = 256 bytes = 32 words
Main memory access time = 20ns(time for first word) + 155ns(time for remaining 31 words, 31*5 = 155ns) = 175 ns
Average access time = h1*t1 + (1-h1)(t1+t2) = t1 +(1-h1)t2
⇒ 3 + (0.06)(175) = 13.5 ns
Question 30 |
Consider the following data path diagram.
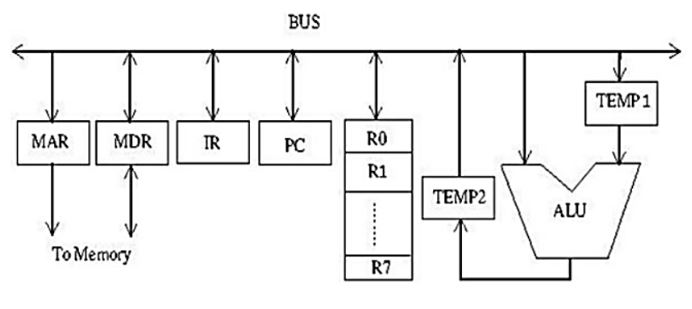
Consider an instruction: R0 ← R1 + R2. The following steps are used to execute it over the given data path. Assume that PC is incremented appropriately. The subscripts r and w indicate read and write operations, respectively.
1. R2r, TEMP1r, ALUadd, TEMP2w 2. R1r, TEMP1w 3. PCr, MARw, MEMr 4. TEMP2r, ROw 5. MDRr, IRw
Which one of the following is the correct order of execution of the above steps?
A | 3, 5, 1, 2, 4
|
B | 3, 5, 2, 1, 4
|
C | 1, 2, 4, 3, 5 |
D | 2, 1, 4, 5, 3
|
First the PC value has to be moved into MAR (step-3 from the given sequence), then the instruction has to be fetched(step-5 from the given sequence). Then Temp1 is loaded with the value of R1 (step-2 from the given sequence), then the addition operation is performed by accessing the R2 value directly and adding it to Temp1 value and storing the result in Temp2 (step-1 from the given sequence).
Finally the result from Temp2 is stored in R0 (step-4 from the given sequence).
Hence the correct sequence is (3, 5, 2, 1, 4).
Question 31 |
Consider a non-pipelined processor operating at 2.5 GHz. It takes 5 clock cycles to complete an instruction. You are going to make a 5-stage pipeline out of this processor. Overheads associated with pipelining force you to operate the pipelined processor at 2 GHz. In a given program, assume that 30% are memory instructions, 60% are ALU instructions and the rest are branch instructions. 5% of the memory instructions cause stalls of 50 clock cycles each due to cache misses and 50% of the branch instructions cause stalls of 2 cycles each. Assume that there are no stalls associated with the execution of ALU instructions. For this program, the speedup achieved by the pipelined processor over the non-pipelined processor (round off to 2 decimal places) is _____.
A | 2.16 |
It is given that each instruction takes 5 clock cycles to execute in the non-pipelined architecture, so time taken to execute each instruction = 5 * 0.4 = 2ns
In the pipelined architecture the clock cycle time = 1/2G = 0.5 ns
In the pipelined architecture there are stalls due to memory instructions and branch instructions.
In the pipeline, the updated clocks per instruction CPI = (1 + stall frequency due to memory operations * stalls of memory instructions + stall frequency due to branch operations * stalls due to branch instructions)
Out of the total instructions , 30% are memory instructions. Out of those 30%, only 5% cause stalls of 50 cycles each.
Stalls per instruction due to memory operations = 0.3*0.05*50 = 0.75
Out of the total instructions 10% are branch instructions. Out of those 10% of instructions 50% of them cause stalls of 2 cycles each.
Stalls per instruction due to branch operations = 0.1*0.5*2 = 0.1
The updated CPI in pipeline = 1 + 0.75 + 0.1 = 1.85
The execution time in the pipeline = 1.85 * 0.5 = 0.925 ns
The speed up = Time in non-pipelined architecture / Time in pipelined architecture = 2 / 0.925 = 2.16
Question 32 |
A computer system with a word length of 32 bits has a 16 MB byte-addressable main memory and a 64 KB, 4-way set associative cache memory with a block size of 256 bytes. Consider the following four physical addresses represented in hexadecimal notation.
A1 = 0x42C8A4, A2 = 0x546888, A3 = 0x6A289C, A4 = 0x5E4880
Which one of the following is TRUE?
A | A1 and A4 are mapped to different cache sets. |
B | A1 and A3 are mapped to the same cache set. |
C | A3 and A4 are mapped to the same cache set. |
D | A2 and A3 are mapped to the same cache set. |
The word length is given as 32 bits and the physical addresses mentioned are all contain 6 hexadecimal digits, so the the physical address is 32 bits long.
Block size is 256 bytes, block offset = 8 bits as it is a byte addressable memory.
Cache size = 64KB
Number of blocks in the cache = 64KB/256B = 256
It is a 4-way set associative cache, so no. of sets in the cache = 256/4 = 64 = 26
In the physical address we need 6 bits for the SET number.
TAG bits = 32 - 6 - 8 = 18
So the 32 bits physical address is divided as (18 TAG bits + 6 SET number bits + 8 OFFSET bits)
Since in all the options we are asked about SET numbers of the given addresses, we need to find the SET number of each of the addresses.
A1 = 0x42C8A4, here SET number is (00 1000) which includes the last 2 bits of C(1100) and binary representation of 8 (1000).
A2 = 0x546888, here SET number is (10 1000) which includes the last 2 bits of 6(0110) and binary representation of 8 (1000).
A3 = 0x6A289C here SET number is (10 1000) which includes the last 2 bits of 2(0010) and binary representation of 8 (1000).
A4 = 0x5E4880 here SET number is (00 1000) which includes the last 2 bits of 4 (0100) and binary representation of 8 (1000).
From the given options option-4 is TRUE as A2, A3 are mapped to the same cache SET.
Question 33 |
A processor has 64 registers and uses 16-bit instruction format. It has two types of instructions: I-type and R-type. Each I-type instruction contains an opcode, a register name, and a 4-bit immediate value. Each R-type instruction contains an opcode and two register names. If there are 8 distinct I-type opcodes, then the maximum number of distinct R-type opcodes is _____.
A | 14 |
All possible binary combinations = 216
There are 64 registers, so no. of bits needed to identify a register = 6
I-type instruction has (Opcode+Register+4-bit immediate value). There are 8 distinct I-type instructions.
All the binary combinations possible with the I-type instructions are = 8*26*24 = 213
R-type instructions have 2 register operands.
Let x be the number of R-type instructions.
All the possible binary combinations of R-type instructions = x*26*26 = x*212
The sum of I-type and R-type binary combinations should be equal to 216.
x*212 + 213 = 216
212 (x+2) = 216
x+2 = 24
x = 16 - 2 = 14
Question 34 |
Relative mode of addressing is most relevant to writing
A | coroutines |
B | position – independent code |
C | shareable code |
D | interrupt handlers |
Question 35 |
Number of machine cycles required for RET instruction in 8085 microprocessor is
A | 1 |
B | 2 |
C | 3 |
D | 5 |
2 for stack operation.
Total no. of cycles = 2+1 = 3
Question 36 |
For the daisy chain scheme of connecting I/O devices, which of the following statements is true?
A | It gives non-uniform priority to various devices. |
B | It gives uniform priority to all devices |
C | It is only useful for connecting slow devices to a processor device. |
D | It requires a separate interrupt pin on the processor for each device. |
→ In this all devices connected serially.
→ High priority devices placed first, followed by low priority devices.
Question 37 |
A micro program control unit is required to generate a total of 25 control signals. Assume that during any microinstruction, at most two control signals are active. Minimum number of bits required in the control word to generate the required control signals will be
A | 2 |
B | 2.5 |
C | 10 |
D | 12 |
= 5+5
= 10 bits
Question 38 |
An 8052 based system has an output port with address 00H. Consider the following assembly language program.
ORG 0100H
MVI A, 00H
LXI H, 0105H
OUT 00H
INR A
PCHL
HLT
(a) What does the program do with respect to the output port 00H?
(b) Show the wave forms at the three least significant bits of the port 00H.
A | Theory Explanation. |
Question 39 |
Consider the following program in pseudo-pascal syntax. What is printed by the program if parameter a in procedure test 1 is passed as
(i) call-by-reference parameter
(ii) call-by-value-result parameter
program Example (input, output)
var b: integer;
procedure test2:
begin b:=10; end
procedure test1 (a:integer):
begin a:=5;
writeln ('point 1: ', a, b);
test2;
writeln ('point 2: ', a, b);
end
begin(*Example*)
b:=3; test1(b);
writeln('point3:', b);
end A | Theory Explanation. |
Question 40 |
A hard disk is connected to a 50 MHz processor through a DMA controller. Assume that the initial set-up of a DMA transfer takes 1000 clock cycles for the processor, and assume that the handling of the interrupt at DMA completion requires 500 clock cycles for the processor. The hard disk has a transfer rate of 2000 Kbytes/sec and average block transferred is 4 K bytes. What fraction of the processor time is consumed by the disk, if the disk is actively transferring 100% of the time?
A | Theory Explanation. |
Question 41 |
A computer system has a three level memory hierarchy, with access time and hit ratios as shown below:
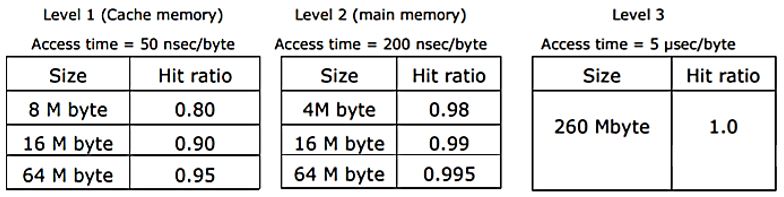
(a) What should be the minimum sizes of level 1 and 2 memories to achieve an average access time of less than 100 nsec?
(b) What is the average access time achieved using the chosen sizes of level 1 and level 2 memories?
A | Theory Explanation. |
Question 42 |
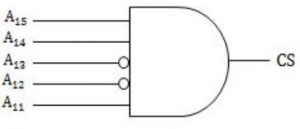
The chip select logic for a certain DRAM chip in a memory system design is shown below. Assume that the memory system has 16 address lines denoted by A15 to A0. What is the range of addresses (in hexadecimal) of the memory system that can get enabled by the chip select (CS) signal?
A | C800 to C8FF |
B | C800 to CFFF |
C | DA00 to DFFF |
D | CA00 to CAFF |
The chip select address for given figure:
A4 - A15 = 25
So, total addressable loactions = 216/25 = 211
211 = 2048 or location 0 to 2047
∴ CFFF - C800 = 2047
Answer is C800 to CFFF.
Question 43 |
A certain processor uses a fully associative cache of size 16 kB. The cache block size is 16 bytes. Assume that the main memory is byte addressable and uses a 32-bit address. How many bits are required for the Tag and the Index fields respectively in the addresses generated by the processor?
A | 28 bits and 0 bits |
B | 24 bits and 4 bits |
C | 24 bits and 0 bits |
D | 28 bits and 4 bits |
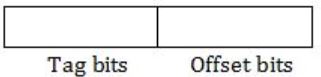
No index bits is there. So, now for tag bits,
Total bits - Offset bits = 32 - 4 = 28
So, tag bits = 28, Index bits = 0
Question 44 |
A certain processor deploys a single-level cache. The cache block size is 8 words and the word size is 4 bytes. The memory system uses a 60-MHz clock. To service a cache miss, the memory controller first takes 1 cycle to accept the starting address of the block, it then takes 3 cycles to fetch all the eight words of the block, and finally transmits the words of the requested block at the rate of 1 word per cycle. The maximum bandwidth for the memory system when the program running on the processor issues a series of read operations is ______ × 106 bytes/sec.
A | 160 |
B | 145 |
C | 172 |
D | 124 |

Cache block = 8 words
Word size = 4 bytes
Cache block size = 32 bytes
Clock = 60 MHz
⇒ T = 1/clock = 1/60×106 seconds
Cache miss
= 1 cycle(Address) + 3 cycles (8 words) + 1word/cycle ×8 (transfer)
= 12 cycles
= 12/60×106
Total bandwidth = total data/total time = 32 bytes/(12/60×106) = 160 × 106 bytes/second
Answer: 160
Question 45 |
RST 7.5 interrupt in 8085 microprocessor executes the interrupt service routine from interrupt vector location
A | 0000H |
B | 0075H |
C | 003CH |
D | 0034H |
→ 60 in hexa decimal is 003CH.
Question 46 |
Purpose of a start bit in RS 232 serial communication protocol is
A | to synchronize receiver for receiving every byte |
B | to synchronize receiver for receiving a sequence of bytes |
C | a parity bit |
D | to synchronize receiver for receiving the last byte |
Question 47 |
The correct matching for the following pairs is
(A) DMA I/O (1) High speed RAM (B) Cache (2) Disk (C) Interrupt I/O (3) Printer (D) Condition Code Register (4) ALU
A | A – 4 B – 3 C – 1 D – 2 |
B | A – 2 B – 1 C – 3 D – 4
|
C | A – 4 B – 3 C – 2 D – 1 |
D | A – 2 B – 3 C – 4 D – 1 |
Cache → High speed RAM
Interrupt I/O → Printer
Condition code register → ALU
Question 48 |
When an interrupt occurs, an operating system
A | ignores the interrupt |
B | always changes state of interrupted process after processing the interrupt |
C | always resumes execution of interrupted process after processing the interrupt
|
D | may change state of interrupted process to 'blocked’ and schedule another process
|
Option B: Not always.
Option C: Not always. If some high priority interrupt comes during execution of current interrupt then it fails.
Option D: It is True always.
Question 49 |
The expression (a*b)* c op....
where 'op' is one of '+', '*' and '↑' (exponentiation) can be evaluated on a CPU with a single register without storing the value of (a * b) if
A | ‘op’ is ’+’ or ‘*’ |
B | ‘op’ is ’↑’ or ‘*’ |
C | ‘op’ is ’↑’ or ‘+’ |
D | not possible to evaluate without storing |
(a*b)*c + d
(a*b)*c * d
(a*b)*c ∧ d
In any case, brackets has the highest priority always. So I have to compute brackets first. Now, for + and *, I can do the rest of the operation and save results in the same register. But for exponentiation, I have to store the result of a*b, then do the computation of c∧d, then multiply these two results.
Hence, (A) is correct.
Question 50 |
Contents of A register after the execution of the following 8085 microprocessor program is
MVI A, 55 H MVI C, 25 H ADD C DAA
A | 7AH |
B | 80H |
C | 50H |
D | 22H |
