Data-Structures
Question 1 |
- There is a main hash table of size 4.
- The 2 least significant bits of a key is used to index into the main hash table.
- Initially, the main hash table entries are empty.
- Thereafter, when more keys are hashed into it, to resolve collisions, the set of all keys corresponding to a main hash table entry is organized as a binary tree that grows on demand.
- First, the 3rd least significant bit is used to divide the keys into left and right subtrees.
- To resolve more collisions, each node of the binary tree is further sub-divided into left and right subtrees based on the 4th least significant bit.
- A split is done only if it is needed, i.e., only when there is a collison.
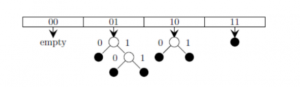
Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
A | 10, 9, 6, 7, 5, 13 |
B | 9, 5, 13, 6, 10, 14 |
C | 9, 5, 10, 6, 7, 1 |
D | 5, 9, 4, 13, 10, 7 |
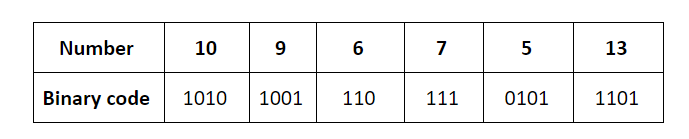
The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.
Question 2 |
push(54); push(52); pop(); push(55); push(62); s=pop();
Consider the following sequence of operations on an empty queue.
enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32); q = dequeue();
The value of s + q is ________
A | 86 |
push(54) ⇒ 54
push(52)=> 54, 52(top)
pop() ⇒ 54 (top)
push(55)==> 54, 55(top)
push(62) ⇒ 54,55,62(top)
s=pop() ⇒ 62 will store into the variable s then s=62
enqueue(21) ⇒ (front) 21(rear)
enqueue(24) ⇒ (Front)21, 24(rear)
dequeue()==> (front) 24(rear)
enqueue(28) ===> (front) 24,28 (rear)
enqueue(32)====>(front) 24,28,32 (rear)
q=dequeue() ⇒ value 24 will store into the variable “q”
q=24
S+q =62+24 =86
Question 3 |
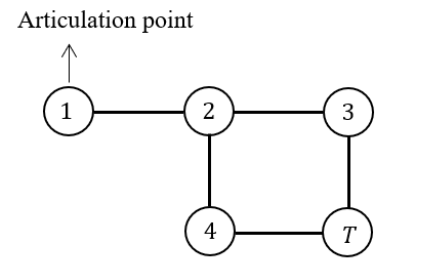
- Root of T can never be an articulation point in G.
- If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
- A leaf of T can be an articulation point in G.
- Root of T is an articulation point in G if and only if it has 2 or more children
A | 4 |
Statement-2:
Example-1:
If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
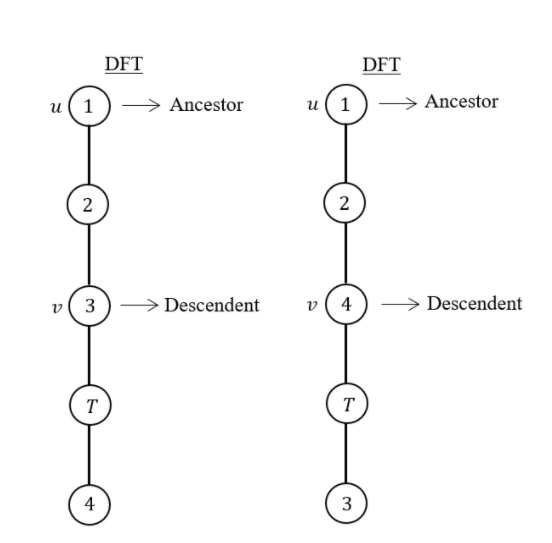
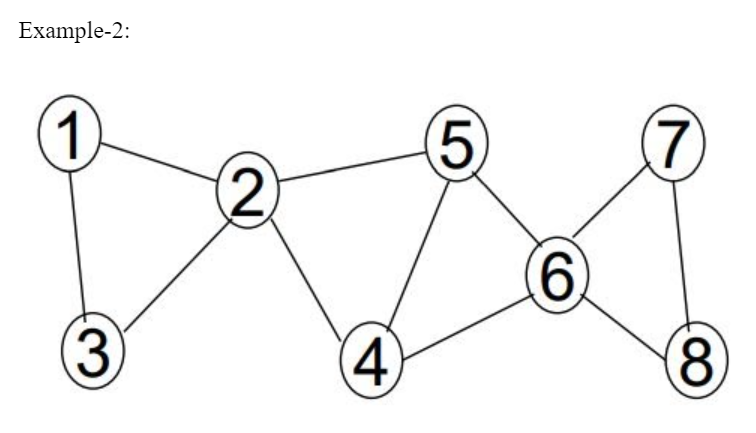

Here 2 and 6 are articulation points. If you consider node-1 ancestor and node-3 descendent, then without passing through from node -2, there exists a path from one node to another node.
Path from node-1 to node-3 If you consider node-5 ancestor and node-4 descendent, then without passing through from node-6, there exists a path from one node to another node.
Path from node-4 to node-5
The given statement is not TRUE for all cases. So, the given statement is FALSE.
Statement-3: FALSE: Leafs of a DFS-tree are never articulation points.
Statement-4: TRUE: The root of a DFS-tree is an articulation point if and only if it has at least two children.
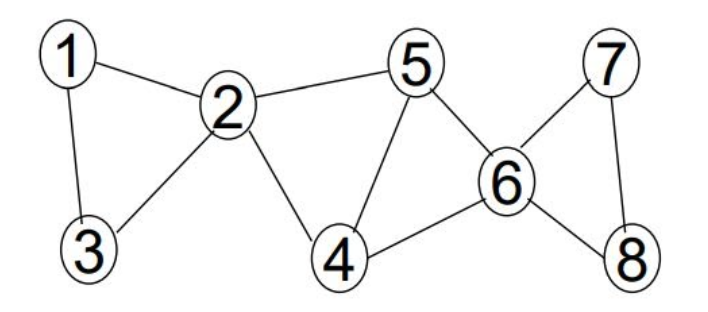
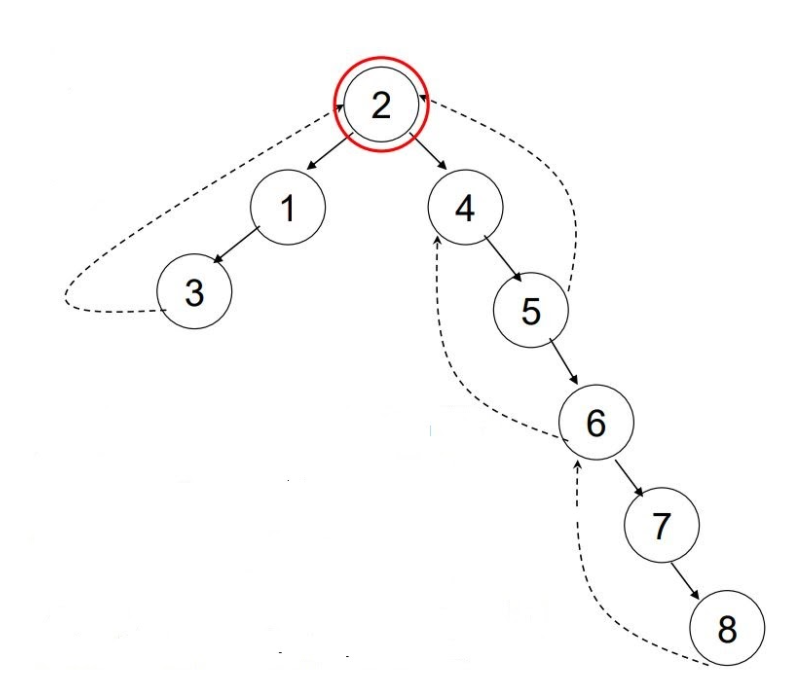
Node 2 is an AP because any node from the first subtree (1, 2) is connected to any node from the second subtree (4, 5, 6, 7, 8) by a path that includes node 2. If node 2 is removed, the 2 subtrees are disconnected.
Question 4 |
S1:The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
S2:The sequence of procedure returns corresponds to a postorder traversal of the activation tree.
Which one of the following options is correct?
A | S1is false and S2is false
|
B | S1is true and S2is true |
C | S1is true and S2is false |
D | S1is false and S2is true |
The given statements are true, they are well known facts.
- The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
- The sequence of returns corresponds to a postorder traversal of the activation tree.
Question 5 |
A |  |
B |  |
C | 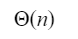 |
D | 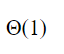 |
The time complexity of searching an element in T that is smaller than the maximum element in T is O(1) time.
Example:
Comparing that 5<10 will take only a constant amount of time.
Question 6 |
Consider a singly linked list having n nodes. The data items d1, d2, ...dn are stored in these n nodes. Let X be a pointer to the j-th node (1≤j≤n) in which dj is stored. A new data item d stored in node with address Y is t be inserted. Give an algorithm to insert d into the list to obtain a list having items d1, d2, ..., dj-1, dj, ..., dn in the order without using the header.
A | Theory Explanation. |
Question 7 |
Prove by the principal of mathematical induction that for any binary tree, in which every non-leaf node has 2 descendants, the number of leaves in the tree is one more than the number of non-leaf nodes.
A | Theory Explanation. |
Question 8 |
A stack is used to pass parameters to procedures in a procedure call.
(a) If a procedure P has two parameters as described in procedure definition:
procedure P (var x :integer; y: integer);
and if P is called by ; P(a,b)
State precisely in a sentence what is pushed on stack for parameters a and b.
(b) In the generated code for the body of procedure P, how will the addressing of formal parameters x and y differ?
A | Theory Explanation. |
Question 9 |
An unrestricted use of the “goto” statement is harmful because
A | it makes it more difficult to verify programs |
B | it increases the running time of the programs |
C | it increases the memory required for the programs
|
D | it results in the compiler generating longer machine code |
Question 10 |
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1, 2, 3, 4, 5 in that order?
A | 3, 4, 5, 1, 2 |
B | 3, 4, 5, 2, 1 |
C | 1, 5, 2, 3, 4 |
D | 5, 4, 3, 1, 2 |
→ Remaining options are not possible.
Question 11 |
Linked lists are not suitable data structures of which one of the following problems?
A | Insertion sort |
B | Binary search |
C | Radix sort |
D | Polynomial manipulation
|
Question 12 |
A rooted tree with 12 nodes has its nodes numbered 1 to 12 in pre-order. When the tree is traversed in post-order, the nodes are visited in the order 3, 5, 4, 2, 7, 8, 6, 10, 11, 12, 9, 1.
Reconstruct the original tree from this information, that is, find the parent of each node, and show the tree diagrammatically.
A | Theory Explanation. |
Question 13 |
A queue Q containing n items and an empty stack S are given. It is required to transfer all the items from the queue to the stack, so that the item at the front of queue is on the top of the stack, and the order of all other items is preserved. Show how this can be done in O(n) time using only a constant amount of additional storage. Note that the only operations which can be performed on the queue and stack are Delete, Insert, Push and Pop. Do not assume any implementation of the queue or stack.
A | Theory Explanation. |
Question 14 |
What is the number of binary trees with 3 nodes which when traversed in postorder give the sequence A, B, C? Draw all these binary trees.
A | Theory Explanation. |
Question 15 |
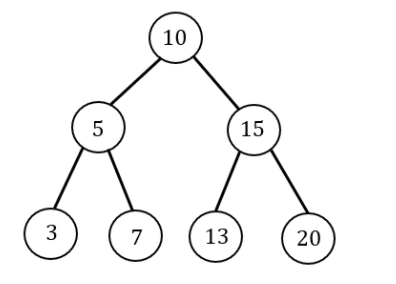
The preorder traversal of a binary search tree is 15, 10, 12, 11, 20, 18, 16, 19.
Which one of the following is the postorder traversal of the tree?
A | 20, 19, 18, 16, 15, 12, 11, 10 |
B | 11, 12, 10, 16, 19, 18, 20, 15
|
C | 10, 11, 12, 15, 16, 18, 19, 20 |
D | 19, 16, 18, 20, 11, 12, 10, 15 |
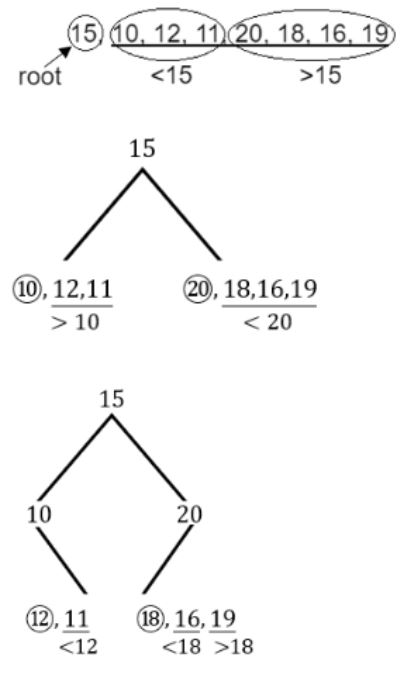

Postorder:
11, 12, 10, 16, 19, 18, 20, 15
Question 16 |
Consider a double hashing scheme in which the primary hash function is h1(k) = k mod 23, and the secondary hash function is h2(k) = 1 + (k mod 19). Assume that the table size is 23. Then the address returned by probe 1 in the probe sequence (assume that the probe sequence begins at probe 0) for key value k=90 is _______.
A | 13 |
• K=90
• h1(k) = k mod 23 = 90 mod 23 = 21
• In case of collision, we need to use secondary hash function.
• h2(k) = 1 + (k mod19) = 1 + 90mod19 = 1+14 = 15
• Now (21+15) mod 23 = 36 mod 23 = 13
• So the address is 13.
Question 17 |
What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order?
A | θ(n log n) |
B | θ(n2) |
C | θ(1) |
D | θ(n) |
Total number of elements inserted into an empty linked list is O(n). So, it will take O(n) time in the worst case.
After inserting elements into an empty linked list we have to perform sorting operation.
To get minimum time complexity to perform sorting order is merge sort. It will give O(nlogn) time complexity only.
Let head be the first node of the linked list to be sorted and head Reference be the pointer to head.
The head in MergeSort as the below implementation changes next links to sort the linked lists (not data at the nodes), so head node has to be changed if the data at the original head is not the smallest value in the linked list.
Note: There are other sorting methods also will give decent time complexity but quicksort will give O(n2) and heap sort will not be suitable to apply.
Question 18 |
Consider the following C program.
#includeint main () { int a [4] [5] = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20}}; printf (“%d\n”, *(*(a+**a+2) +3)); return (0); }
The output of the program is _______.
A | 19 |
#include
int main()
{
int a[4][5] = { {1,2,3,4,5},
{6,7,8,9,10},
{11,12,13,14,15},
{16,17,18,19,20}
};
printf("%d\n",a); //880 (consider base address = 880)
printf("%d\n",*a); //880
printf("%d\n",**a); //1
printf("%d\n",**a+2); //3
printf("%d\n",a+**a+2); //940
printf("%d\n",*(a+**a+2));//940
printf("%d\n",*(a+**a+2)+3);//952
printf("%d\n",*(*(a+**a+2)+3));//19
return 0;
}

Question 19 |
What is the worst case time complexity of inserting n2 elements into an AVL-tree with n elements initially?
A | θ(n4)
|
B | θ(n2)
|
C | θ(n3) |
D | θ(n2 log n) |
In question they asked about n2 elements.
So, In worst case it will take o(n2 log n) time.
Question 20 |
Let G = (V,E) be a directed, weighted graph with weight function w:E → R. For some function f:V → R, for each edge (u,v) ∈ E, define w'(u,v) as w(u,v) + f(u) - f(v).
Which one of the options completes the following sentence so that it is TRUE?
“The shortest paths in G under w are shortest paths under w’ too, _______”.
A | if and only if f(u) is the distance from s to u in the graph obtained by adding a new vertex s to G and edges of zero weight from s to every vertex of G |
B | if and only if ∀u ∈ V, f(u) is positive
|
C | if and only if ∀u ∈ V, f(u) is negative |
D | for every f: V→R |


Question 21 |
In a balanced binary search tree with n elements, what is the worst case time complexity of reporting all elements in range [a,b]? Assume that the number of reported elements is k.
A | θ(n log k) |
B | θ(log n + k) |
C | θ(k log n) |
D | θ(log n) |
Time complexity of the above program is O(h + k) where h is the height of BST and k is the number of nodes in a given range.
Here h is log n, hence O(log n+k).
Question 22 |
Consider the array representation of a binary min-heap containing 1023 elements. The minimum number of comparisons required to find the maximum in the heap is _______.
A | 511 |
n=1023
= Ceil(1023/2)
= 512
So, the maximum element is also part of n/2.
So, we have to subtract from the total elements
= 512-1
= 511
Question 23 |
Consider the following statements:
- (i) First-in-first out types of computations are efficiently supported by STACKS.
(ii) Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
(iii) Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
(iv) Last-in-first-out type of computations are efficiently supported by QUEUES.
Which of the following is correct?
A | (ii) and (iii) are true |
B | (i) and (ii) are true |
C | (iii) and (iv) are true |
D | (ii) and (iv) are true |
(iv) LIFO computation efficiently supported by stacks.
Then given (i) and (iv) are false.
Answer:- A
Question 24 |
An advantage of chained hash table (external hashing) over the open addressing scheme is
A | Worst case complexity of search operations is less? |
B | Space used is less |
C | Deletion is easier |
D | None of the above |
Question 25 |
In the balanced binary tree in the below figure, how many nodes will become unbalanced when a node is inserted as a child of the node “g”?

A | 1 |
B | 3 |
C | 7 |
D | 8 |
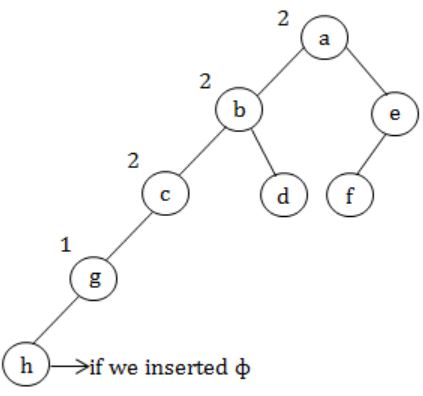
a, b, c are going to unbalance.
Question 26 |
Which of the following sequences denotes the post order traversal sequence of the tree of question 14?
A | f e g c d b a |
B | g c b d a f e |
C | g c d b f e a |
D | f e d g c b a |
Left → Right → Root
g c d b f e a
Question 27 |
The minimum number of interchanges needed to convert the array
89, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70
into a heap with the maximum element at the root is
A | 0 |
B | 1 |
C | 2 |
D | 3 |

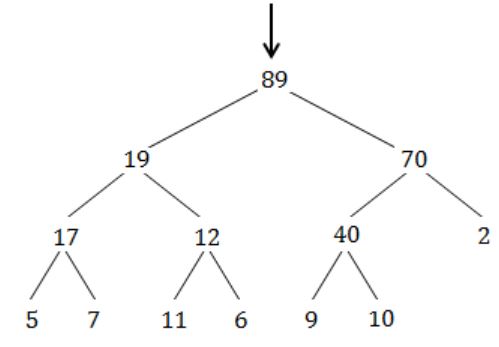
Question 28 |
A binary search tree is generated by inserting in order the following integers:
50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24
The number of nodes in the left subtree and right subtree of the root respectively is
A | (4, 7) |
B | (7, 4) |
C | (8, 3) |
D | (3, 8) |
So greater than 50 will be in right subtree of 50 and less than 50 in left subtree.
So, answer will be (7, 4).
Question 29 |
A binary search tree is used to locate the number 43. Which of the following probe sequences are possible and which are not? Explain.
A | 61 52 14 17 40 43 |
B | 2 3 50 40 60 43 |
C | 10 65 31 48 37 43 |
D | 81 61 52 14 41 43 |
E | 17 77 27 66 18 43 |
Question 30 |
I. The smallest element in a max-heap is always at a leaf node.
II. The second largest element in a max-heap is always a child of the root node.
III. A max-heap can be constructed from a binary search tree in Θ(n) time.
IV. A binary search tree can be constructed from a max-heap in Θ(n) time.
Which of the above statements are TRUE?
A | I, II and III |
B | II, III and IV |
C | I, III and IV |
D | I, II and IV |
(ii) TRUE: The second smallest element in a heap is always a child of root node.
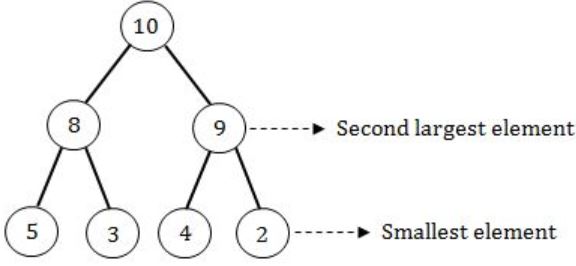
(iii) TRUE: Converting from binary search tree to max heap will take O(n) time as well as O(n) space complexity.
(iv) FALSE: We can’t convert max heap to binary search tree in O(n) time.
Question 31 |
Let T be a full binary tree with 8 leaves. (A full binary tree has every level full). Suppose two leaves a and b of T are chosen uniformly and independently at random. The expected value of the distance between a and b in T (i.e., the number of edges in the unique path between a and b) is (rounded off to 2 decimal places) _____.
A | 5.54 |
B | 1.34 |
C | 4.25 |
D | 3.82 |
A node can be chosen twice and the path from that node to itself will be zero.
∴ Path 1 = 0
Similarly,
Path 2 = 2
Path 3 = 4
Path 4 = 4
Path 5 = 6
Path 6 = 6
Path 7 = 6
Path 8 = 6
∴ Expected value = Σ Path length × Probability of selecting path
= 2×1/8 + 4×2/8 + 6×4/8 + 0×1/8
= 1/4 + 1/1 + 3/1 + 0
= 4 + 1/4
= 17/4
= 4.25
Question 32 |
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list should be used?
A | Singly linked list |
B | Doubly linked list |
C | Circular doubly linked list |
D | Array implementation of list |
Question 33 |
Which of the following is essential for converting an infix expression to the postfix from efficiently?
A | An operator stack |
B | An operand stack |
C | An operand stack and an operator stack |
D | A parse tree |
An operand stack ⇒ Postfix to Prefix
Operator & operand stack ⇒ We don't use two stacks
Parse tree ⇒ No use
Question 34 |
A binary search tree contains the value 1, 2, 3, 4, 5, 6, 7, 8. The tree is traversed in pre-order and the values are printed out. Which of the following sequences is a valid output?
A | 5 3 1 2 4 7 8 6 |
B | 5 3 1 2 6 4 8 7 |
C | 5 3 2 4 1 6 7 8 |
D | 5 3 1 2 4 7 6 8 |
Option D:
Let draw binary search tree for the given sequence,
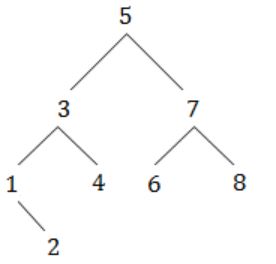
After traversing through this tree we will get same sequence.
Question 35 |
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
A | non-increasing order |
B | non-decreasing order |
C | strictly increasing order |
D | strictly decreasing order |
Question 36 |
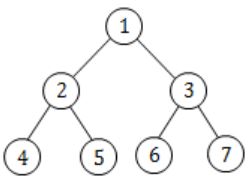
Which of the following statements is false?
A | A tree with a n nodes has (n – 1) edges |
B | A labeled rooted binary tree can be uniquely constructed given its postorder and preorder traversal results |
C | A complete binary tree with n internal nodes has (n + 1) leaves |
D | Both B and C |
D: The maximum no. of nodes in a binary tree of height h is 2h+1 - 1.
h=2 ⇒ 23 - 1 ⇒ 7
Question 37 |
A complete n-ary tree is one in which every node has 0 or n sons. If x is the number of internal nodes of a complete n-ary tree, the number of leaves in it is given by
A | x(n-1) + 1 |
B | xn - 1 |
C | xn + 1 |
D | x(n+1) |
Let no. of leaf nodes = L
Let nt be total no. of nodes.
So, L+x = nt -----(I)
Also for n-ary tree with x no. of internal nodes, total no. of nodes is,
nx+1 = nt -----(II)
So, equating (I) & (II),
L+x = nx+1
L = x(n-1) + 1
Question 38 |
Let A be a two dimensional array declared as follows:
A: array [1 ... 10] [1 ... 15] of integer;
Assuming that each integer takes one memory location, the array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element a[i][j]?
A | 15i + j + 84 |
B | 15j + i + 84 |
C | 10i + j + 89 |
D | 10j + i + 89 |
100 + 15 * (i-1) + (j-1)
= 100 + 15i - 15 + j - 1
= 15i + j + 84
Question 39 |
Faster access to non-local variables is achieved using an array of pointers to activation records called a
A | stack |
B | heap |
C | display |
D | activation tree |
→ Use a pointer array to store the activation records along the static chain.
→ Fast access for non-local variables but may be complicated to maintain.
Question 40 |
Let p be a pointer as shown in the figure in a single linked list.

What do the following assignment statements achieve?
- q: = p → next
p → next:= q → next
q → next:=(q → next) → next
(p → next) → next:= q
(b) Compute the postfix equivalent of the following Infix expression
3 * log(x+1) - a/2
A | Theory Explanation. |
Question 41 |
Draw the binary tree with node labels a, b, c, d, e, f and g for which the inorder and postorder traversals result in the following sequences:
Inorder a f b c d g e Postorder a f c g e d b
A | Theory Explanation. |
Question 42 |
(a) Derive a recurrence relation of the size of the smallest AVL tree with height h.
(b) What is the size of the smallest AVL tree with height 8.A | Theory Explanation. |
Question 43 |
The number of articulation points of the following graph is

A | 0 |
B | 1 |
C | 2 |
D | 3 |
Total no. of articulation points = 3
Question 44 |
(a) In a binary tree, a nil node is defined to be a node with 2 children. Use induction on the height of the binary tree to prove that the number of full nodes plus one is equal to the number of leaves.
(b) Draw a min-heap that results from insertion of the following elements in order into an initially empty min-heap: 7, 6, 5, 4, 2, 3, 1. Show the result after the deletion of the root of this heap.
A | Theory Explanation. |
Question 45 |
The most appropriate matching for the following pairs
X: depth first search 1: heap
Y: breadth-first search 2: queue
Z: sorting 3: stack
is
A | X – 1 Y – 2 Z – 3 |
B | X – 3 Y – 1 Z – 2 |
C | X – 3 Y – 2 Z – 1 |
D | X – 2 Y – 3 Z – 1 |
Queue is used in breadth-first search.
Heap is used in heap.
Question 46 |
Consider the following nested representation of binary trees: (X Y Z) indicates Y and Z are the left and right sub stress, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree?
A | (1 2 (4 5 6 7)) |
B | (1 (2 3 4) 5 6) 7) |
C | (1 (2 3 4) (5 6 7)) |
D | (1 (2 3 NULL) (4 5)) |

(Proper Representation)
Question 47 |
Suppose you are given an array s[1...n] and a procedure reverse (s,i,j) which reverses the order of elements in a between positions i and j (both inclusive). What does the following sequence do, where 1 ≤ k ≤ n:
reverse(s, 1, k) ;
reverse(s, k + 1, n);
reverse(s, l, n); A | Rotates s left by k positions |
B | Leaves s unchanged |
C | Reverses all elements of s |
D | None of the above |
Question 48 |
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always tree?
A | LASTIN = LASTPOST |
B | LASTIN = LASTPRE |
C | LASTPRE = LASTPOST |
D | None of the above |
But in case of complete binary last level need not to be full in that case LASTPRE is not equal to LASTIN.
Question 49 |
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let ν be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
A | {u, v} must be an edge in G, and u is a descendant of v in T |
B | {u, v} must be an edge in G, and v is a descendant of u in T |
C | If {u, v} is not an edge in G then u is a leaf in T |
D | If {u, v} is not an edge in G then u and v must have the same parent in T |
In DFS after visiting u, there is no child node then back tracking is happen and then visit the node v. There is no need of (u,v) be an edge.
Question 50 |
Suppose a stack implementation supports, in addition to PUSH and POP, an operation REVERSE, which reverses the order of the elements on the stack.
(a) To implement a queue using the above stack implementation, show how to implement ENQUEUE using a single operation and DEQUEUE using a sequence of 3 operations.
(b) The following postfix expression, containing single digit operands and arithmetic operators + and *, is evaluated using a stack.
5 2 * 3 4 + 5 2 * * +
Show the contents of the stack.
- (i) After evaluating 5 2 * 3 4 +
(ii) After evaluating 5 2 * 3 4 + 5 2
(iii) At the end of evaluation.
A | Theory Explanation is given below. |
Dequeue → reverse, pop, reverse
(b) (i) After evaluating 5 2 * 3 4 +
Sol:
7(3+4) 10(5*2)
(ii) After evaluating 5 2 * 3 4 + 5 2
Sol:
25(5*5) 7(3+4) 10(5*2)
(iii) At the end of evaluation
Sol: 80
