TIFR PHD 2022
Question 1 |
A snail crawls up a vertical pole 75 feet high, starting from the ground. Each day it crawls up 5 feet, and each night it slides down 4 feet. When will it first reach the top of the pole?
75th day | |
74th day | |
73th day | |
72th day | |
71th day |
Question 2 |
We would like to invite a minimum number n of people (their birthdays are independent of each other) to a party such that the expected number of pairs of people that share the same birthday is at least 1. What should n be?
(Ignore leap years, so there are only 365 possible birthdays. Assume that birthdays fall with equal probability on each of the 365 days of the year.)
(Ignore leap years, so there are only 365 possible birthdays. Assume that birthdays fall with equal probability on each of the 365 days of the year.)
23 | |
28 | |
92 | |
183 | |
366 |
Question 3 |
A binary string is a sequence of 0’s and 1’s. A binary string is finite if the sequence is finite, otherwise it is infinite. Examples of finite binary strings include 00010100, and 1111101010. Which of the following is TRUE about the set of all finite binary strings and the set of all infinite binary strings?
The set of all finite binary strings is countable while the set of all infinite binary strings is uncountable | |
The set of all finite binary strings is uncountable while the set of all infinite binary strings is countable | |
The set of all finite binary strings and the set of all infinite binary strings are both countable | |
The set of all finite binary strings and the set of all infinite binary strings are both uncountable | |
The set of all finite binary strings is countable while whether the set of all infinite binary strings is countable or not is not known |
Question 4 |
Consider the polynomial p(x) = x3 − x2 + x − 1. How many symmetric matrices with integer entries are there whose characteristic polynomial is p? (Recall that the characteristic polynomial of a square matrix A in the variable x is defined to be the determinant of the matrix (A − xI) where I is the identity matrix.)
0 | |
1 | |
2 | |
4 |
Question 5 |
Let F be the set of all functions mapping {1, . . . , n} to {1, . . . ,m}. Let f be a function that is chosen uniformly at random from F. Let x, y be distinct elements from the set {1, . . . , n}. Let p denote the probability that f(x) = f(y). Then,
p = 0 | |
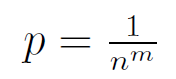 | |
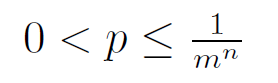 | |
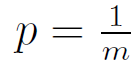 | |
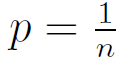 |
Question 6 |
Let f be a polynomial of degree n ≥ 3 all of whose roots are non-positive real numbers. Suppose that f(1) = 1. What is the maximum possible value of f′(1)?
1 | |
n | |
n+1 | |
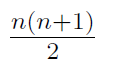 | |
f′(1) can be arbitrarily large given only the constraints in the question |
Question 7 |
Initially, N white beads are arranged in a circle. A number k is chosen uniformly at random from {1, . . . ,N − 1}. Then a set of k beads is chosen uniformly from the white beads, and these k beads are coloured black. The position of the beads remains unchanged. What is the probability that the black beads occur sequentially in the circle, i.e., at most two black beads have white beads next to them?
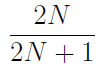 | |
 | |
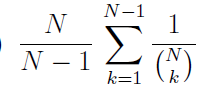 | |
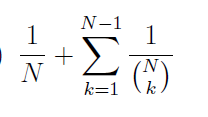 | |
None of the above |
Question 8 |
Let A be the (n + 1) × (n + 1) matrix given below, where n ≥ 1. For i ≤ n, the i-th row of A has every entry equal to 2i − 1 and the last row, i.e., the (n + 1)-th row of A has every entry equal to −n2.
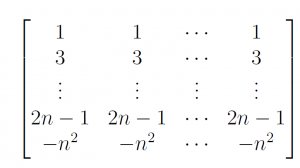
Which of the following statements is TRUE for all n ≥ 1?
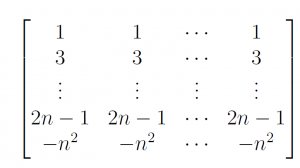
Which of the following statements is TRUE for all n ≥ 1?
A has rank n | |
A2 has rank 1 | |
All the eigenvalues of A are distinct | |
All the eigenvalues of A are 0 | |
None of the above |
Question 9 |
You are given the following properties of sets A, B, X, and Y . For notation, |A| denotes the cardinality of set A (i.e., the number of elements in A), and A \ B
denotes the set of elements that are in A but not in B.
1. A ∪ B = X ∪ Y
2. A ∩ B = X ∩ Y = ∅
3. |Y \ A| = 2
4. |A \ X| = 4
Which of the following statements MUST then be FALSE?
1. A ∪ B = X ∪ Y
2. A ∩ B = X ∩ Y = ∅
3. |Y \ A| = 2
4. |A \ X| = 4
Which of the following statements MUST then be FALSE?
|X| = 5 | |
|Y | = 5 | |
|A ∪ X| = |B ∪ Y | | |
|A ∩ X| = |B ∩ Y | | |
|A| = |B| |
Question 10 |
Consider a bag containing colored marbles. There are n marbles in the bag such that there is exactly one pair of marbles of color i for each i ∈ {1, . . . ,m} and the rest of the marbles are of distinct colors (different from colors {1, . . . ,m}). You draw two marbles uniformly at random (without replacement). What is the probability that both marbles are of same color?
 | |
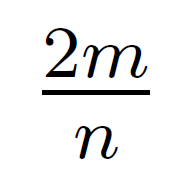 | |
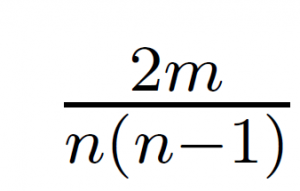 | |
 | |
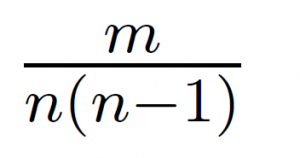 |
Question 11 |
Let X be a finite set. A family F of subsets of X is said to be upward closed if the following holds for all sets A,B ⊆ X:
A ∈ F and A ⊆ B ⇒ B ∈ F.
For families F and G of subsets of X, let
F ⊔ G = {A ∪ B : A ∈ F and B ∈ G}.
Suppose F and G are upward closed families. Then which of the following is true?
A ∈ F and A ⊆ B ⇒ B ∈ F.
For families F and G of subsets of X, let
F ⊔ G = {A ∪ B : A ∈ F and B ∈ G}.
Suppose F and G are upward closed families. Then which of the following is true?
F ⊔ G = F ∩ G | |
F ⊔ G = F ∪ G | |
F ⊔ G = F \ G | |
F ⊔ G = G \ F | |
None of the above |
There are 11 questions to complete.
