TIFR PHD CS & SS 2018
Question 1 |
Consider a point A inside a circle C that is at distance 9 from the centre of the circle. Suppose you are told that there is a chord of length 24 passing through A with A as its midpoint. How many distinct chords of C have integer length and pass through
2 | |
6 | |
7 | |
12 | |
14 |
Question 2 |
Consider the following subsets of R3 (the first two are cylinders, the third is a plane):
C1 = {(x, y, z) : y2 + z2 ≤ 1};
C2 = {(x, y, z) : x2 + z2 ≤ 1};
H = {(x, y, z) : z = 0.2}.
Let A = C1 ∩ C2 ∩ H. Which of the following best describes the shape of the set A?
C1 = {(x, y, z) : y2 + z2 ≤ 1};
C2 = {(x, y, z) : x2 + z2 ≤ 1};
H = {(x, y, z) : z = 0.2}.
Let A = C1 ∩ C2 ∩ H. Which of the following best describes the shape of the set A?
Circle | |
Ellipse | |
Triangle | |
Square | |
An octagonal convex figure with curved sides |
Question 3 |
Which of the following statements is TRUE for all sufficiently large integers n?
22√(log log n) < 2 < √(log n) < n | |
2√(log n) < n < 22√(log log n) | |
n < 2√(log n) < 22√(log log n) | |
n < 22√(log log n) < 2√(log n) < | |
2√(log n) < 22√(log log n) < n |
Question 4 |
The distance from your home to your office is 4 kilometres and your normal walking
speed is 4 km/hr. On the first day, you walk at your normal walking speed and take
time T1 to reach office.
On the second day, you walk at a speed of 3 km/hr for 2 kilometres, and at a speed of 5 km/hr for the remaining 2 kilometres and you take time T2 to reach office.
On the third day, you walk at a speed of 3 km/hr for 30 minutes, and at 5 km/hr for the remaining time and take time T3 to reach office.
What can you say about the ordering of T1, T2 and T3?
On the second day, you walk at a speed of 3 km/hr for 2 kilometres, and at a speed of 5 km/hr for the remaining 2 kilometres and you take time T2 to reach office.
On the third day, you walk at a speed of 3 km/hr for 30 minutes, and at 5 km/hr for the remaining time and take time T3 to reach office.
What can you say about the ordering of T1, T2 and T3?
T1 > T2 and T1 < T3. | |
T1 = T2 = T3 | |
T1 < T2 and T1 < T3 | |
T1 = T2 and T1 < T3 | |
T1 < T2 and T1 = T3 |
Question 5 |
Which of the following is the derivative of f(x) = xx when x > 0?
xx | |
xx In x | |
xx + xx In x | |
(xx)(xxIn x) | |
None of the above; function is not differentiable for x > 0 |
Question 6 |
What is the minimum number of students needed in a class to guarantee that there
are at least 6 students whose birthdays fall in the same month?
6 | |
23 | |
61 | |
72 | |
91 |
Question 7 |
Consider the following function definition.
void greet (int n)
{
if (n>0)
{
printf("hello");
greet(n-1);
}
printf("world");
}
If you run greet(n) for some non-negative integer n, what would it print?
void greet (int n)
{
if (n>0)
{
printf("hello");
greet(n-1);
}
printf("world");
}
If you run greet(n) for some non-negative integer n, what would it print?
n times “hello”, followed by n + 1 times “world” | |
n times “hello”, followed by n times “world” | |
n times “helloworld” | |
n + 1 times “helloworld” | |
n times “helloworld”, followed by “world” |
Question 8 |
A crime has been committed with four people at the scene of the crime. You are
responsible for finding out who did it. You have recorded the following statements
from the four witnesses, and you know one of them has committed the crime.
(1) Anuj says that Binky did it.
(2) Binky says that Anuj did it.
(3) Chacko says that Binky is telling the truth.
(4) Desmond says that Chacko is not lying.
You know that exactly three of the statements recorded are FALSE. Who committed the crime?
(1) Anuj says that Binky did it.
(2) Binky says that Anuj did it.
(3) Chacko says that Binky is telling the truth.
(4) Desmond says that Chacko is not lying.
You know that exactly three of the statements recorded are FALSE. Who committed the crime?
Anuj | |
Binky | |
Chacko | |
Desmond | |
Either Anuj or Binky; the information is insufficient to pinpoint the criminal |
Question 9 |
How many ways are there to assign colours from the range {1, 2, . . . , r} to the vertices of the following graph so that adjacent vertices receive distinct colours?

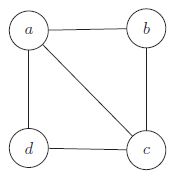
r4 | |
r4-4r3 | |
r4-5r3+8r2-4r | |
r4-4r3+9r2-3r | |
r4-5r3+10r2-15r |
Question 10 |
Let C be a biased coin such that the probability of a head turning up is p. Let
pn denote the probability that an odd number of heads occurs after n tosses for n∈{0,1,2, . . . }. Then, which of the following is TRUE?
pn = 1/2 for all n ∈ {0, 1, 2, . . . }. | |
pn =(1-p)(1-pn-1+p.pn-1 for n≥1 and p0=0 | |
pn =Σni-1(1-2p)I-1 for n ≥ 1. | |
If p = 1/2, then pn = 1/2 for all n ∈ {0, 1, 2, . . . }. | |
pn = 1 if n is odd and 0 otherwise. |
Question 11 |
We are given a (possibly empty) set of objects. Each object in the set is colored
either black or white; is shaped either circular or rectangular, and has a profile that is either fat or thin. These properties obey the following principles:
1. Each white object is also circular.
2. Not all thin objects are black.
3. Each rectangular object is also either thin or white or both thin and white.
Consider the following statements:
(i) If there is a thin object in the set, then there is also a white object.
(ii) If there is a rectangular object in the set, then there are at least two objects.
(iii) Every fat object in the set is circular.
Which of the above statements must be TRUE for the set?
1. Each white object is also circular.
2. Not all thin objects are black.
3. Each rectangular object is also either thin or white or both thin and white.
Consider the following statements:
(i) If there is a thin object in the set, then there is also a white object.
(ii) If there is a rectangular object in the set, then there are at least two objects.
(iii) Every fat object in the set is circular.
Which of the above statements must be TRUE for the set?
(i) only | |
(i) and (ii) only | |
(i) and (iii) only | |
None of the statements must be TRUE | |
All of the statements must be TRUE |
There are 11 questions to complete.
