ISRO-2018
Question 1 |
The difference between a named pipe and a regular file in Unix is that
Unlike a regular file, named pipe is a special file | |
The data in a pipe is transient, unlike the content of a regular file | |
Pipes forbid random accessing, while regular files do allow this. | |
All of the above |
Question 1 Explanation:
→ Named pipe is a special instance of a file that has no contents on the filesystem.
→ A FIFO special file (a named pipe) is similar to a pipe, except that it is accessed as part of the filesystem. It can be opened by multiple processes for reading or writing. When processes are exchanging data via the FIFO, the kernel passes all data internally without writing it to the filesystem. Thus, the FIFO special file has no contents on the filesystem; the filesystem entry merely serves as a reference point so that processes can access the pipe using a name in the filesystem.
→ The kernel maintains exactly one pipe object for each FIFO special file that is opened by at least one process. The FIFO must be opened on both ends (reading and writing) before data can be passed. Normally, opening the FIFO blocks until the other end is opened also.
→ A FIFO special file (a named pipe) is similar to a pipe, except that it is accessed as part of the filesystem. It can be opened by multiple processes for reading or writing. When processes are exchanging data via the FIFO, the kernel passes all data internally without writing it to the filesystem. Thus, the FIFO special file has no contents on the filesystem; the filesystem entry merely serves as a reference point so that processes can access the pipe using a name in the filesystem.
→ The kernel maintains exactly one pipe object for each FIFO special file that is opened by at least one process. The FIFO must be opened on both ends (reading and writing) before data can be passed. Normally, opening the FIFO blocks until the other end is opened also.
Question 2 |
A class of 30 students occupy a classroom containing 5 rows of seats, with 8 seats in each row. If the students seat themselves at random, the probability that the sixth seat in the fifth row will be empty is
1/5 | |
1/3 | |
1/4 | |
2/5 |
Question 2 Explanation:
Step-1: Given, 5 rows with 8 seats in each row.
Total number of seats = 5*40
= 40 seats
Total number of students= 30
Step-2: Given constraint that, 6th seat in the fifth row is empty
When we are deleting 6th seat, 30 students have 39 choices of seats
Step-3: Total number of choices = 39C30
Total ways to choose = 40C30
Step-4: Final probability = 39C30 / 40C30
= 1/4
Total number of seats = 5*40
= 40 seats
Total number of students= 30
Step-2: Given constraint that, 6th seat in the fifth row is empty
When we are deleting 6th seat, 30 students have 39 choices of seats
Step-3: Total number of choices = 39C30
Total ways to choose = 40C30
Step-4: Final probability = 39C30 / 40C30
= 1/4
Question 3 |
The domain of the function log( log sin(x) ) is
0 < x < π | |
2nπ < x < (2n+1)π , for n in N | |
Empty set | |
None of the above |
Question 3 Explanation:
→ The range of sinx value lies between -1 and 1 and whereas log(sinx) value will be the positive value.
→ So the domain of log(log sin(x)) is undefined which is empty Set.
→ So the domain of log(log sin(x)) is undefined which is empty Set.
Question 4 |
The following paradigm can be used to find the solution of the problem in minimum time:
Given a set of non-negative integer, and a value K, determine if there is a subset of the given set with the sum equal to K:
Divide and Conquer | |
Dynamic Programming | |
Greedy Algorithm | |
Branch and Bound |
Question 4 Explanation:
The above problem clearly specifies that sum of subset problem. The sum of the subset problem using recursion will give exponential time. Using dynamic programming we can get pseudo-polynomial time.
Sum of subset problem:
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with the sum equal to the given sum.
Example:
Array set[ ]= {1,2,3,4,5} and sum=6
Here there are possible subsets (2,4),(1,2,3) and (5,1).
Sum of subset problem:
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with the sum equal to the given sum.
Example:
Array set[ ]= {1,2,3,4,5} and sum=6
Here there are possible subsets (2,4),(1,2,3) and (5,1).
Question 5 |
( G, *) is an abelian group. Then
x = x-1, for any x belonging to G | |
x = x2, for any x belonging to G | |
(x * y )2 = x2 * y2, for any x, y belonging to G | |
G is of finite order |
Question 5 Explanation:
An abelian group is a commutative group. As per the above options, option C is the correct answer because it follows commutative property.
(x * y )2 = x2 * y2, for any x, y belonging to G
(x * y )2 = x2 * y2, for any x, y belonging to G
Question 6 |
Consider the following C code segment:

For the program fragment above, which of the following statements about the variables i and j must be true after the execution of this program? [!(exclamation) sign denotes factorial in the Solution]

For the program fragment above, which of the following statements about the variables i and j must be true after the execution of this program? [!(exclamation) sign denotes factorial in the Solution]
( j=(x-1)!) ∧ (i>=x) | |
( j = 9!) ∧ (i =10) | |
(( j = 10!) ∧ (i = 10 )) V (( j = (x - 1)!) ∧ (i = x )) | |
(( j = 9!) ∧ (i = 10)) V (( j = (x - 1)!) ∧ (i = x )) |
Question 6 Explanation:
As per code segment,
Step-1: The ith loop will compute from value 1 to 9. If the condition is true, then it computes j=j*i statement.
Step-2: The statement j=j*i is nothing but calculating 9!. If the condition fails automatically while loop will be terminated. It means maximum we can execute 9 values.
Step-3: when x becomes 10 then maximum I value will be 9. So, we can calculate up to 9! And I become 10 then it terminates the condition.
Step-1: The ith loop will compute from value 1 to 9. If the condition is true, then it computes j=j*i statement.
Step-2: The statement j=j*i is nothing but calculating 9!. If the condition fails automatically while loop will be terminated. It means maximum we can execute 9 values.
Step-3: when x becomes 10 then maximum I value will be 9. So, we can calculate up to 9! And I become 10 then it terminates the condition.
Question 7 |
A computer uses ternary system instead of the traditional binary system. An n bit string in the binary system will occupy
3+n ternary digits | |
2n/3 ternary digits | |
n(log23) ternary digits | |
n(log32 ) ternary digits |
Question 7 Explanation:
→ Binary numbers are maximum 2n-1.
→ But in question they are given ternary numbers, it means 3x-1.
→ Both will take different no. of bits to represent the same number.
3x -1 = 2n -1
3x = 2n
Apply log on both side
x= log3( 2n)
x=n*log32 .
→ But in question they are given ternary numbers, it means 3x-1.
→ Both will take different no. of bits to represent the same number.
3x -1 = 2n -1
3x = 2n
Apply log on both side
x= log3( 2n)
x=n*log32 .
Question 8 |
Which of the following is application of Breadth First Search on the graph?
Finding the diameter of the graph | |
Finding the bipartite graph | |
Both (a) and (b) | |
None of the above |
Question 8 Explanation:
Breadth-first search can be used to solve many problems in graph theory
Examples
1. Copying garbage collection, Cheney's algorithm
2. Find the diameter of the graph
3. Testing bipartiteness of a graph.
4. Finding the shortest path between two nodes u and v, with path length measured by the number of edges (an advantage over depth-first search)
5. (Reverse) Cuthill–McKee mesh numbering
6. Ford–Fulkerson method for computing the maximum flow in a flow network
7. Serialization/Deserialization of a binary tree vs serialization in sorted order, allows the tree to be reconstructed in an efficient manner.
8. Construction of the failure function of the Aho-Corasick pattern matcher.
Examples
1. Copying garbage collection, Cheney's algorithm
2. Find the diameter of the graph
3. Testing bipartiteness of a graph.
4. Finding the shortest path between two nodes u and v, with path length measured by the number of edges (an advantage over depth-first search)
5. (Reverse) Cuthill–McKee mesh numbering
6. Ford–Fulkerson method for computing the maximum flow in a flow network
7. Serialization/Deserialization of a binary tree vs serialization in sorted order, allows the tree to be reconstructed in an efficient manner.
8. Construction of the failure function of the Aho-Corasick pattern matcher.
Question 9 |
Micro program is
The name of a source program in microcomputers | |
Set of micro instructions that define the individual operations in response to a machine-language instruction | |
A primitive form of macros used in assembly language programming | |
A very small segment of machine code |
Question 9 Explanation:
→ The Microprogram is computing a sequence of microinstructions that controls the operation of an arithmetic and logic unit so that machine code instructions are executed.
→ The Microprogram is set of microinstructions that define the individual operations in response to a machine-language instruction
→ The Microprogram is set of microinstructions that define the individual operations in response to a machine-language instruction
Question 10 |
Given two sorted list of size m and n respectively. The number of comparisons needed the worst case by the merge sort algorithm will be
m*n | |
maximum of m and n | |
minimum of m and n | |
m+n–1 |
Question 10 Explanation:
Here the maximum number of comparisons is m+n-1.
For example: Take 2 sub-arrays of size 3 such as 1,3,5 and another subarray 2,4,6. Then in this case number of comparisons is 5 which is m+n-1 can be taken as O(m+n).
For example: Take 2 sub-arrays of size 3 such as 1,3,5 and another subarray 2,4,6. Then in this case number of comparisons is 5 which is m+n-1 can be taken as O(m+n).
Question 11 |
In unit testing of a module, it is found that for a set of test data, at the maximum 90% of the code alone were tested with the probability of success 0.9. The reliability of the module is
Greater than 0.9 | |
Equal to 0.9 | |
At most 0.81 | |
At least 0.81 |
Question 11 Explanation:
Given data
Step-1: 90% of code were tested,
Testing with the probability=0.9
Step-2: We can write tested data into 0.9 because it is given in percentages.
Step-3: Reliability of the module = Tested data * probability
= 0.9 * 0.9
= 0.81(at most)
Step-1: 90% of code were tested,
Testing with the probability=0.9
Step-2: We can write tested data into 0.9 because it is given in percentages.
Step-3: Reliability of the module = Tested data * probability
= 0.9 * 0.9
= 0.81(at most)
Question 12 |
In a file which contains 1 million records and the order of the tree is 100, then what is the maximum number of nodes to be accessed if B+ tree index is used?
5 | |
4 | |
3 | |
10 |
Question 12 Explanation:
Explanation:
→ If there are K search-key values in the file, the path is no longer than ⌈log⌈n/2⌉(K)⌉.
→ A node is generally the same size as a disk block, typically 4 kilobytes, and n is typically around 100 (40 bytes per index entry).
→ With 1 million search key values and n = 100, at most log50(1000000)=4 nodes are accessed in a lookup.
Note: Contrast this with a balanced binary free with 1 million search key values around 20 nodes are accessed in a lookup. Above difference is significant since every node access may need a disk I/O, costing around 20 milliseconds!
→ If there are K search-key values in the file, the path is no longer than ⌈log⌈n/2⌉(K)⌉.
→ A node is generally the same size as a disk block, typically 4 kilobytes, and n is typically around 100 (40 bytes per index entry).
→ With 1 million search key values and n = 100, at most log50(1000000)=4 nodes are accessed in a lookup.
Note: Contrast this with a balanced binary free with 1 million search key values around 20 nodes are accessed in a lookup. Above difference is significant since every node access may need a disk I/O, costing around 20 milliseconds!
Question 13 |
A particular disk unit uses a bit string to record the occupancy or vacancy of its tracks, with 0 denoting vacant and 1 for occupied. A 32-bit segment of this string has hexadecimal value D4FE2003. The percentage of occupied tracks for the corresponding part of the disk, to the nearest percentage is
12 | |
25 | |
38 | |
44 |
Question 14 |
Which of the following is a dense index?
Primary index | |
Clusters index | |
Secondary index | |
secondary non-key index |
Question 14 Explanation:
→ The primary index is created for the primary key of a table. So, records are usually clustered according to the primary key. It can be sparse.
→ In the sparse index, index records are not created for every search key. An index record here contains a search key and an actual pointer to the data on the disk. To search a record, we first proceed by index record and reach the actual location of the data. If the data we are looking for is not where we directly reach by following the index, then the system starts a sequential search until the desired data is found.
→ The secondary index usually dense.
→ In the dense index, there is an index record for every search key value in the database. This makes searching faster but requires more space to store index records itself. Index records contain search key value and a pointer to the actual record on the disk.
→ In the sparse index, index records are not created for every search key. An index record here contains a search key and an actual pointer to the data on the disk. To search a record, we first proceed by index record and reach the actual location of the data. If the data we are looking for is not where we directly reach by following the index, then the system starts a sequential search until the desired data is found.
→ The secondary index usually dense.
→ In the dense index, there is an index record for every search key value in the database. This makes searching faster but requires more space to store index records itself. Index records contain search key value and a pointer to the actual record on the disk.
Question 15 |
In E-R model, Y is the dominant entity and X is a subordinate entity
If X is deleted, then Y is also deleted | |
If Y is deleted, then X is also deleted | |
If Y is deleted, then X is not deleted | |
None of the above |
Question 15 Explanation:
→ It is the best example of referential integrity. In referential integrity, we are using a foreign key.
→ If we want to delete any entity in the dominant entity(Like primary key of a table) then subordinate entity(derived attribute) also deleted.
Note: If we want to delete any subordinate entity in entity then the dominant entity is not going to delete.
→ If we want to delete any entity in the dominant entity(Like primary key of a table) then subordinate entity(derived attribute) also deleted.
Note: If we want to delete any subordinate entity in entity then the dominant entity is not going to delete.
Question 16 |
Of the following, which best characterizes computers that use memory-mapped I/O?
The computer provides special instructions for manipulating I/O ports | |
I/O ports are placed at addresses on the bus and are accessed just like other memory locations | |
To perform I/O operations, it is sufficient to place the data in an address register and call channel to perform the operation | |
I/O can be performed only when memory management hardware is turned on |
Question 16 Explanation:
→ Memory-mapped I/O uses the same address space to address both memory and I/O devices.
→ The memory and registers of the I/O devices are mapped to (associated with) address values.
→ So when an address is accessed by the CPU, it may refer to a portion of physical RAM, or it can instead refer to the memory of the I/O device. Thus, the CPU instructions used to access the memory can also be used for accessing devices.
→ Each I/O device monitors the CPU's address bus and responds to any CPU access of an address assigned to that device, connecting the data bus to the desired device's hardware register.
→ To accommodate the I/O devices, areas of the addresses used by the CPU must be reserved for I/O and must not be available for normal physical memory.
→ The reservation may be permanent, or temporary (as achieved via bank switching).
→ The memory and registers of the I/O devices are mapped to (associated with) address values.
→ So when an address is accessed by the CPU, it may refer to a portion of physical RAM, or it can instead refer to the memory of the I/O device. Thus, the CPU instructions used to access the memory can also be used for accessing devices.
→ Each I/O device monitors the CPU's address bus and responds to any CPU access of an address assigned to that device, connecting the data bus to the desired device's hardware register.
→ To accommodate the I/O devices, areas of the addresses used by the CPU must be reserved for I/O and must not be available for normal physical memory.
→ The reservation may be permanent, or temporary (as achieved via bank switching).
Question 17 |
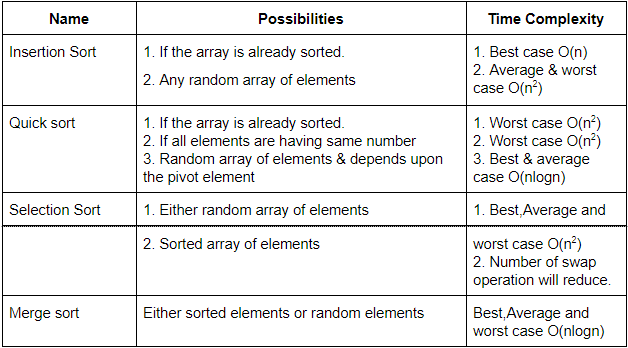
Of the following sorting algorithms, which has a running time that is least dependent on the initial ordering of the input?
Merge Sort | |
Insertion Sort | |
Selection Sort | |
Quick Sort |
Question 17 Explanation:
Question 18 |

I. Increase the rate at which requests are satisfied (throughput)
II. Decrease the likelihood of deadlock
III. Increase the ease of achieving a correct implementation
III Only | |
II Only | |
I Only | |
II and III Only |
Question 18 Explanation:
It only satisfied statement I. because increasing the memory size increases the rate at which requests are satisfied but can not alter the possibility of deadlock and neither does it play any role in implementation.
Question 19 |

style="font-weight: 400;">Where Fwd and Bwd represent forward and a backward link to the adjacent elements of the list. Which of the following segments of code deletes the node pointed to by X from the doubly linked list, if it is assumed that X points to neither the first nor the last node of the list?
X→ Bwd→ Fwd = X→ Fwd; X→ Fwd → Bwd = X→ Bwd ; | |
X→ Bwd.Fwd = X→ Fwd ; X.Fwd→ Bwd = X→ Bwd ; | |
X.Bwd→ Fwd = X.Bwd ; X→ Fwd.Bwd = X.Bwd ; | |
X→ Bwd→ Fwd = X→ Bwd ; X→ Fwd→ Bwd = X→ Fwd; |
Question 19 Explanation:
Let the element just before x be y and that just after be z. In order to link y to z,
we need x→ Bwd→ Fwd = x.
Fwd and in order to link z to y, we need x→ Fwd→ Bwd=x→ Bwd.
we need x→ Bwd→ Fwd = x.
Fwd and in order to link z to y, we need x→ Fwd→ Bwd=x→ Bwd.
Question 20 |
If Tree-1 and Tree-2 are the trees indicated below :
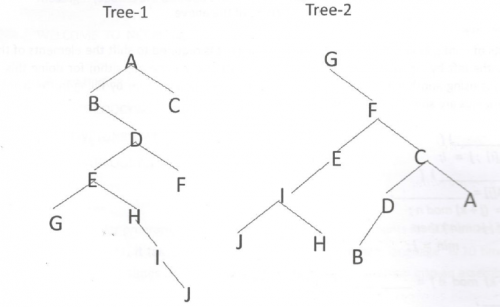
Which traversals of Tree-1 and Tree-2, respectively, will produce the same sequence?

Which traversals of Tree-1 and Tree-2, respectively, will produce the same sequence?
Preorder, Postorder | |
Postorder, Inorder | |
Postorder, Preorder | |
Inorder, Preorder |
Question 20 Explanation:
→ Pre order traverses Root, Left, Right.
→ Post order traverses Left, Right, Root.
→ In-order traverses Left, Root, Right.
Tree-1: Post order: GJIHEFBDCA
Tree-2: In order: GJIHEFBDCA
→ Post order traverses Left, Right, Root.
→ In-order traverses Left, Root, Right.
Tree-1: Post order: GJIHEFBDCA
Tree-2: In order: GJIHEFBDCA
There are 20 questions to complete.
