GATE 2004
Question 1 |
The goal of structured programming is to:
have well indented programs
| |
be able to infer the flow of control from the compiled code
| |
be able to infer the flow of control from the program text
| |
avoid the use of GOTO statements |
Question 2 |
Consider the following C function.
void swap (int a, int b)
{
int temp;
temp = a;
a = b;
b = temp;
}
In order to exchange the values of two variables x and y.
call swap (x, y)
| |
call swap (&x, &y)
| |
swap (x,y) cannot be used as it does not return any value
| |
swap (x,y) cannot be used as the parameters are passed by value
|
Here parameters passed by value in C then there is no change in the values.
Option B:
Here values are not swap.
Here parameters are passed by address in C.
Option C:
It is false. Return value is not valid for exchanging the variables.
Option D:
It is correct.
We cannot use swap(x,y) because parameters are passed by value.
Only exchanging the values (or) variables are passing their address and then modify the content with the help of dereferencing operator(*).
Question 3 |
A single array A[1..MAXSIZE] is used to implement two stacks. The two stacks grow from opposite ends of the array. Variables top1 and top2 (topl < top2) point to the location of the topmost element in each of the stacks. If the space is to be used efficiently, the condition for “stack full” is
(top1 = MAXSIZE/2) and (top2 = MAXSIZE/2+1)
| |
top1 + top2 = MAXSIZE
| |
(top1 = MAXSIZE/2) or (top2 = MAXSIZE)
| |
top1 = top2 – 1 |
Question 4 |
The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree (the height is the maximum distance of a leaf node from the root)?
2 | |
3 | |
4 | |
6 |

Height of the binary search tree = 3
Question 5 |
The best data structure to check whether an arithmetic expression has balanced parentheses is a
queue | |
stack | |
tree | |
list |
While evaluating when left parentheses occur then it push in to the stack, when right parentheses occur pop from the stack.
While at the end there is empty in the stack.
Question 6 |
Level order traversal of a rooted tree can be done by starting from the root and performing
preorder traversal | |
in-order traversal | |
depth first search | |
breadth first search |
It is an algorithm for traversing (or) searching tree (or) graph data structures. It starts at the root and explores all of the neighbour nodes at the present depth prior to moving on to the nodes at the next depth level.
Question 7 |
Given the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199) and the hash function x mod 10, which of the following statements are true?
-
i) 9679, 1989, 4199 hash to the same value
ii) 1471, 6171 hash to the same value
iii) All elements hash to the same value
iv) Each element hashes to a different value
i only | |
ii only | |
i and ii only | |
iii or iv |
Hash function = x mod 10
Hash values = (2, 4, 1, 9, 9, 1, 3, 9)
9679, 1989, 4199 have same hash values
&
1471, 6171 have same hash values.
Question 8 |
Which of the following grammar rules violate the requirements of an operator grammar? P,Q,R are nonterminals, and r,s,t are terminals.
- (i) P → Q R
(ii) P → Q s R
(iii) P → ε
(iv) P → Q t R r
(i) only | |
(i) and (iii) only | |
(ii) and (iii) only | |
(iii) and (iv) only |
i) On RHS it contains two adjacent non-terminals.
ii) Have nullable values.
Question 9 |
Consider a program P that consists of two source modules M1 and M2 contained in two different files. If M1 contains a reference to a function defined in M2, the reference will be resolved at
Edit time | |
Compile time | |
Link time | |
Load time |
Question 10 |
Consider the grammar rule E → E1 - E2 for arithmetic expressions. The code generated is targeted to a CPU having a single user register. The subtraction operation requires the first operand to be in the register. If E1 and E2 do not have any common sub expression, in order to get the shortest possible code
E1 should be evaluated first
| |
E2 should be evaluated first | |
Evaluation of E1 and E2 should necessarily be interleaved | |
Order to evaluation of E1 and E2 is of no consequence
|
Question 11 |
Consider the following statements with respect to user-level threads and kernel supported threads
- (i) context switch is faster with kernel-supported threads
(ii) for user-level threads, a system call can block the entire process
(iii) Kernel supported threads can be scheduled independently
(iv) User level threads are transparent to the kernel
Which of the above statements are true?
(ii), (iii) and (iv) only | |
(ii) and (iii) only | |
(i) and (iii) only | |
(i) and (ii) only |
→ If one user level thread perform blocking operation then entire process will be blocked. Option B is true.
→ User level threads are threads are transparent to the kernel. Because user level threads are created by users. Option D is true.
→ Kernel supported threads can be scheduled independently, that is based on OS. Option C is true.
Question 12 |
Consider an operating system capable of loading and executing a single sequential user process at a time. The disk head scheduling algorithm used is First Come First Served (FCFS). If FCFS is replaced by Shortest Seek Time First (SSTF), claimed by the vendor to give 50% better benchmark results, what is the expected improvement in the I/O performance of user programs?
50% | |
40% | |
25% | |
0% |
→ The better vendor benchmark results doesn't effects the I/O performance.
→ In FCFS (or) SSTF only one choice is to choose for IO from multiple IO's. There is always one I/O at a time.
Question 13 |
Let R1(A,B,C) and R2(D,E) be two relation schema, where the primary keys are shown underlined, and let C be a foreign key in R1 referring to R2. Suppose there is no violation of the above referential integrity constraint in the corresponding relation instances r1 and r2. Which one of the following relational algebra expressions would necessarily produce an empty relation?
ΠD(r2) - ΠC(r1) | |
ΠC(r1) - ΠD(r2) | |
ΠD(r1⨝C≠Dr2) | |
ΠC(r1⨝C=Dr2) |
→ Based on referral integrity C is subset of values in R2 then,
ΠC(r1) - ΠD(r2) results empty relation.
Question 14 |
Consider the following relation schema pertaining to a students database:
Student (rollno, name, address) Enroll (rollno, courseno, coursename)
Where the primary keys are shown underlined. The number of tuples in the Student and Enroll tables are 120 and 8 respectively. What are the maximum and minimum number of tuples that can be present in (Student * Enroll), where '*' denotes natural join ?
8, 8 | |
120, 8 | |
960, 8 | |
960, 120 |
→ In the question only enroll Id's are same with the student table.
→ The no. of minimum and maximum tuples is same i.e., 8, 8.
Question 15 |
Choose the best matching between Group 1 and Group 2.
Group-1 Group-2
P. Data link 1. Ensures reliable transport of data
over a physical point-to-point link
Q. Network layer 2. Encoder/decodes data for physical
transmission
R. Transport layer 3. Allows end-to-end communication
between two processes
4. Routes data from one network
node to the nextP - 1, Q - 4, R - 3 | |
P - 2, Q - 4, R - 1
| |
P - 2, Q - 3, R - 1 | |
P - 1, Q - 3, R - 2 |
Transport Layer :: Fourth layer of the OSI Model, Responsible for Service point addressing/Socket to socket connection or end to end connection with full reliability.
Network Layer :: Third layer of the OSI Model, Responsible for Host to Host.
Question 16 |
Which of the following is NOT true with respect to a transparent bridge and a router?
Both bridge and router selectively forward data packets
| |
A bridge uses IP addresses while a router uses MAC addresses
| |
A bridge builds up its routing table by inspecting incoming packets | |
A router can connect between a LAN and a WAN |
Question 17 |
The Boolean function x'y' + xy + x'y is equivalent to
x' + y' | |
x + y | |
x + y' | |
x' + y |
= x'y' + x'y + xy
= x'(y'+y)+xy
= x'⋅1+xy
= x'+xy
= (x'+x)(x'+y)
= 1⋅(x'+y)
= x'+y
Question 18 |
In an SR latch made by cross-coupling two NAND gates, if both S and R inputs are set to 0, then it will result in
Q = 0, Q' = 1 | |
Q = 1, Q' = 0 | |
Q = 1, Q' = 1 | |
Indeterminate states |
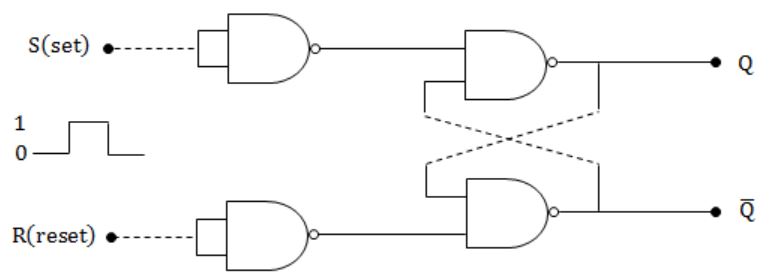
Truth table for the SR latch by cross coupling two NAND gates is
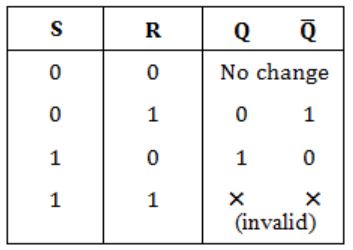
So, Answer is Option (D).
Question 19 |
If 73x (in base-x number system) is equal to 54y (in base-y number system), the possible values of x and y are
8, 16 | |
10, 12 | |
9, 13 | |
8, 11 |
7x+3 = 5y+4
7x-5y = 1
Only option (D) satisfies above equation.
Question 20 |
Which of the following addressing modes are suitable for program relocation at run time?
(i) Absolute addressing (ii) Based addressing (iii) Relative addressing (iv) Indirect addressing
(i) and (iv) | |
(i) and (ii) | |
(ii) and (iii) | |
(i), (ii) and (iv)
|
A fixed address in memory which indicates a location by specifying a distance from another location. In this displacement type addressing is preferred.
So, option A is false.
Based Addressing:
This scheme is used by computers to control access to memory. In this pointers are replaced by protected objects which can be executed by kernel (or) some other privileged process authors.
So, this is suitable for program relocation at runtime.
Relative Addressing:
The offset of the relative addressing is to allow reference to code both before and after the instruction.
This is also suitable.
Indirect Addressing:
Which leads to extra memory location which can be not suitable at run time.
This is not suitable.
→ Only Based Addressing and Relative Addressing are suitable.
Question 21 |
he minimum number of page frames that must be allocated to a running process in a virtual memory environment is determined by
the instruction set architecture | |
page size | |
physical memory size | |
number of processes in memory |
→ An ISA permits multiple implementations that may vary in performance, physical size and monetary cost.
Question 22 |
How many 8-bit characters can be transmitted per second over a 9600 baud serial communication link using asynchronous mode of transmission with one start bit, eight data bits, two stop bits, and one parity bit?
600 | |
800 | |
876 | |
1200 |
So bit rate is 9600 bps.
To send one char we need to send (1 + 8 + 2 +1) = 12
So total char send = 9600 / 12 = 800
