GATE 2000
Question 1 |
The minimum number of cards to be dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are from some same suit is
3 | |
8 | |
9 | |
12 |
No. of suits = 4(P)
Apply pigeon hole principal.
Then number of pigeons = n
floor [(n-1)/P] + 1 = 3
floor [(n-1)/P] = 2
floor [(n-1)] = 8
floor (n) = 8 + 1
n ≥ 9
Minimum no. of cards, n = 9
Question 2 |
An n x n array v is defined as follows:
v[i,j] = i-j for all i,j, 1 ≤ i ≤ n, 1 ≤ j ≤ n
The sum of the elements of the array v is
0 | |
n -1 | |
n2 - 3n + 2 | |
n2 (n+1)/2 |
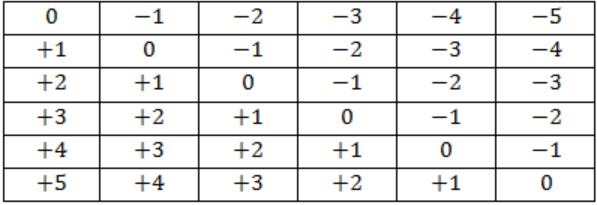
Add ith row and jth column if we zero, apply to all row and their corresponding column the total becomes zero.
Question 3 |
The determinant of the matrix is

is:
4 | |
0 | |
15 | |
20 |
Question 4 |
Let S and T be language over Σ = {a,b} represented by the regular expressions (a+b*)* and (a+b)*, respectively. Which of the following is true?
S ⊂ T | |
T ⊂ S | |
S = T | |
S ∩ T = ɸ |
Question 5 |
Let L denotes the language generated by the grammar S → 0S0/00.
Which of the following is true?
L = 0+ | |
L is regular but not 0+ | |
L is context free but not regular | |
L is not context free |
Question 6 |
The number 43 in 2’s complement representation is
01010101 | |
11010101 | |
00101011 | |
10101011 |
Question 7 |
To put the 8085 microprocessor in the wait state
lower the HOLD input | |
lower the READY input | |
raise the HOLD input | |
raise the READY input |
Question 8 |
Comparing the time T1 taken for a single instruction on a pipelined CPU with time T2 taken on a non-pipelined but identical CPU, we can say that
T1 ≤ T2 | |
T1 ≥ T2 | |
T1 < T2 | |
T1 is T2 plus the time taken for one instruction fetch cycle |
Pipelining is an implementation technique where multiple instructions are overlapped in execution. It has a high throughput (amount of instructions executed per unit time). In pipelining, many instructions are executed at the same time and execution is completed in fewer cycles. The pipeline is filled by the CPU scheduler from a pool of work which is waiting to occur. Each execution unit has a pipeline associated with it, so as to have work pre-planned. The efficiency of pipelining system depends upon the effectiveness of CPU scheduler.
NON- PIPELINING SYSTEM:
All the actions (fetching, decoding, executing of instructions and writing the results into the memory) are grouped into a single step. It has a low throughput.
Only one instruction is executed per unit time and execution process requires more number of cycles. The CPU scheduler in the case of non-pipelining system merely chooses from the pool of waiting work when an execution unit gives a signal that it is free. It is not dependent on CPU scheduler.
Question 9 |
The 8085 microprocessor responds to the present of an interrupt
as soon as the TRAP pin becomes ‘high’ | |
by checking the TRAP pin for ‘high’ status at the end of each instruction each | |
by checking the TRAP pin for ‘high’ status at the end of the execution of each instruction | |
by checking the TRAP pin for ‘high’ status at regular intervals |
Question 10 |
The most appropriate matching for the following pairs
X: Indirect addressing 1 : Loops
Y: Immediate addressing 2 : Pointers
Z: Auto decrement addressing 3: Constants is
X – 3 Y – 2 Z - 1 | |
X – 1 Y – 3 Z - 2 | |
X – 2 Y – 3 Z - 1 | |
X – 3 Y – 1 Z - 2 |
Indirect addressing means that the address of the data is held in an intermediate location so that the address is first 'looked up' and then used to locate the data itself.
Immediate addressing:
Immediate Addressing. An immediate operand has a constant value or an expression. When an instruction with two operands uses immediate addressing, the first operand may be a register or memory location, and the second operand is an immediate constant.
Auto increment or decrements can be one by using loops.
Question 11 |
The following C declarations
struct node
{
int i;
float j;
};
struct node *s[10]; define s to be
An array, each element of which is a pointer to a structure of type node | |
A structure of 2 fields, each field being a pointer to an array of 10 elements | |
A structure of 3 fields: an integer, a float, and an array of 10 elements | |
An array, each element of which is a structure of type node |
Question 12 |
The most appropriate matching for the following pairs
X: m=malloc(5); m= NULL; 1: using dangling pointers
Y: free(n); n->value=5; 2: using uninitialized pointers
Z: char *p; *p = ’a’; 3. lost memory is:
X – 1 Y – 3 Z – 2 | |
X – 2 Y – 1 Z – 3 | |
X – 3 Y – 2 Z – 1 | |
X – 3 Y – 1 Z – 2 |
Y → n is pointer to invalid memory, a making it as a dangling pointer.
Z → p is not initialized.
p = malloc (size of(char))p = malloc (size of(char)); should have been used before assigning 'aa' to ∗p.
Question 13 |
The most appropriate matching for the following pairs
X: depth first search 1: heap
Y: breadth-first search 2: queue
Z: sorting 3: stack is
X – 1 Y – 2 Z – 3 | |
X – 3 Y – 1 Z – 2 | |
X – 3 Y – 2 Z – 1 | |
X – 2 Y – 3 Z – 1 |
Queue is used in breadth-first search.
Heap is used in heap.
Question 14 |
Consider the following nested representation of binary trees: (X Y Z) indicates Y and Z are the left and right sub stress, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree?
(1 2 (4 5 6 7)) | |
(1 (2 3 4) 5 6) 7) | |
(1 (2 3 4) (5 6 7)) | |
(1 (2 3 NULL) (4 5)) |

(Proper Representation)
Question 15 |
Let s be a sorted array of n integers. Let t(n) denote the time taken for the most efficient algorithm to determined if there are two elements with sum less than 1000 in s. Which of the following statements is true?
t(n) is O(1) | |
n ≤ t(n) ≤ n log2 n | |
n log2 n ≤ t(n) < (n/2) | |
t(n) = (n/2) |
Question 16 |
Aliasing in the context of programming languages refers to
multiple variables having the same memory location | |
multiple variables having the same value | |
multiple variables having the same identifier | |
multiple uses of the same variable |
Question 17 |
Consider the following C declaration
struct {
short s [5]
union {
float y;
long z;
} u;
} t; Assume that objects of the type short, float and long occupy 2 bytes, 4 bytes and 8 bytes, respectively. The memory requirement for variable t, ignoring alignment considerations, is
22 bytes | |
14 bytes | |
18 bytes | |
10 bytes |
max[float, long] = max [4, 8] = 8
Total = short[5] + max[float,long] = 10 + 8 = 18
