GATE 2007
Question 1 |
Consider the following two statements about the function f(x)=|x|
P. f(x) is continuous for all real values of x Q. f(x) is differentiable for all real values of x
Which of the following is TRUE?
P is true and Q is false. | |
P is false and Q is true. | |
Both P and Q are true. | |
Both P and Q are false. |
→ f(x) is continuous for all real values of x
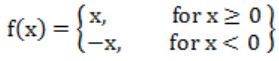
For every value of x, there is corresponding value of f(x).
For x is positive, f(x) is also positive
x is negative, f(x) is positive.
So, f(x) is continuous for all real values of x.
→ f(x) is not differentiable for all real values of x. For x<0, derivative is negative
x>0, derivative is positive.
Here, left derivative and right derivatives are not equal.
Question 2 |
Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S are:
n and n | |
n2 and n | |
n2 and 0 | |
n and 1 |
→ Reflexive
→ Symmetric
→ Transitive
Let a set S be,
S = {1, 2, 3}
Now, the smallest relation which is equivalence relation is,
S×S = {(1,1), (2,2), (3,3)}
= 3
= n (for set of n elements)
And, the largest relation which is equivalence relation is,
S×S = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)}
= 9
= 32
= n2 (for set of n elements)
Question 3 |
What is the maximum number of different Boolean functions involving n Boolean variables?
n2 | |
2n | |
22n | |
2n2 |
Number of variables= n
Number of input combinations is 2n.
Each “boolean” function has two possible outputs i.e 0 and 1.
Number of boolean functions possible is 22n.
Formula: The number of m-ary functions possible with n k-ary variables is mkn.
Question 4 |
Let G be the non-planar graph with the minimum possible number of edges. Then G has
9 edges and 5 vertices | |
9 edges and 6 vertices | |
10 edges and 5 vertices | |
10 edges and 6 vertices |
if n ≥ 3 then e ≤ 3n-6 (for planarity)
where n = no. of vertices
e = no. of edges
Now lets check the options.
A) e=9, n=5
9 ≤ 3(5) - 6
9 ≤ 15 - 6
9 ≤ 9
Yes, it is planar.
B) e=9, n=6
9 ≤ 3(6) - 6
9 ≤ 18 - 6 9 ≤ 12 Yes, it is planar.
iii) e=10, n=5
10 ≤ 3(5) - 6
10 ≤ 15 - 6
10 ≤ 9 No, it is not planar.
So, option C is non-planar graph.
iv) e=10, n=6
10 ≤ 3(6) - 6
10 ≤ 18 - 6
10 ≤ 12
Yes, it is planar.
Question 5 |
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
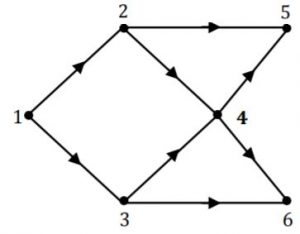
1 2 3 4 5 6 | |
1 3 2 4 5 6 | |
1 3 2 4 6 5 | |
3 2 4 1 6 5 |
(i) Go with vertex with indegree 0.
(ii) Then remove that vertex and also remove the edges going from it.
(iii) Repeat again from (i) till every vertex is completed.
Now we can see that in option (D), '3' is given first which is not possible because indegree of vertex '3' is not zero.
Hence option (D) is not topological ordering.
Question 6 |
Which of the following problems is undecidable?
Membership problem for CFGs. | |
Ambiguity problem for CFGs. | |
Finiteness problem for FSAs. | |
Equivalence problem for FSAs. |
Question 7 |
Which of the following is TRUE?
Every subset of a regular set is regular. | |
Every finite subset of a non-regular set is regular. | |
The union of two non-regular sets is not regular.
| |
Infinite union of finite sets is regular. |
Every subset of regular set is regular, is false. For example L = {an bn | n ≥ 0} is subset of ∑* and L is CFL, whereas ∑* is regular. Hence, every subset of regular set need not be regular.
The union of two non-regular sets is not regular, is also a false statement.
For example, consider two CFL’s.
L = {an bn | n ≥ 0} and its complement Lc = {am bn | m ≠ n } U b*a*.
If we take UNION of L and Lc , we will get ∑*, which is regular. Hence the UNION of two non-regular set may or may not be regular.
The statement, Infinite union of finite sets is regular is also a false statement.
Question 8 |
How many 3-to-8 line decoders with an enable input are needed to construct a 6-to-64 line decoder without using any other logic gates?
7 | |
8 | |
9 | |
10 |
So, we can say that
8 lines covered by ----- 1 decoder
1 line covered by ----- 1/8 decoder
64 lines covered by ----- 64/8 = 8 decoders
8 lines covered by ----- 8/8 = 1 decoder
Hence total no. of decoder needed is,
8 + 1 = 9 decoders.
Question 9 |
Consider the following Boolean function of four variables:
f(w,x,y,z) = ∑(1,3,4,6,9,11,12,14)The function is:
independent of one variable. | |
independent of two variables. | |
independent of three variables. | |
dependent on all the variables. |
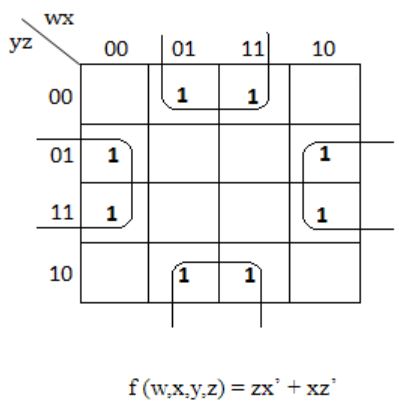
w and y are not needed to represent the function f. So f is independent of two variables.
Question 10 |
Consider a 4-way set associative cache consisting of 128 lines with a line size of 64 words. The CPU generates a 20-bit address of a word in main memory. The number of bits in the TAG, LINE and WORD fields are respectively:
9, 6, 5 | |
7, 7, 6 | |
7, 5, 8 | |
9, 5, 6 |
Each line size 64 words, so no. of bits for WORD = 6 bits
Because it is 4-way set associative cache, no. of sets in the cache = 128/4 = 32 = 25
No. of bits for the set number = 5
Because the address is 20-bits long, no. of TAG bits = 20-5-6 = 9
Question 11 |
Consider a disk pack with 16 surfaces, 128 tracks per surface and 256 sectors per track. 512 bytes of data are stored in a bit serial manner in a sector. The capacity of the disk pack and the number of bits required to specify a particular sector in the disk are respectively:
256 Mbyte, 19 bits | |
256 Mbyte, 28 bits | |
512 Mbyte, 20 bits | |
64 Gbyte, 28 bit |
So the disk pack capacity = 16 * 128 * 256 * 512 bytes = 256 MB
To specify a sector we need the information about surface number, track number and sector number within a track. Surface number needs 4 bits as there are 16 surfaces(24), track number needs 7 bits as there are 128 tracks(27) within a surface, within a track the sector number needs 8 bits as there are 256 sectors (28). Total number bits needed to specify a particular sector = 4+7+8 = 19 bits. Hence option A is the answer.
Question 12 |
The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is:
2h−1 | |
2h−1 – 1 | |
2h+1– 1 | |
2h+1 |
1, 3, 7, 15, 31, ... = 2h+1 - 1
Question 13 |
The maximum number of binary trees that can be formed with three unlabeled nodes is:
1 | |
5 | |
4 | |
3 |
Total no. of possible trees is 5.
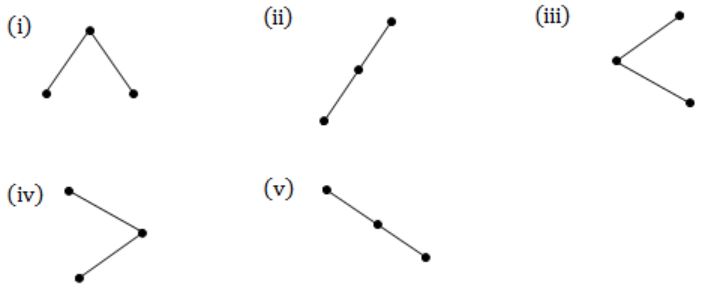
Total = 5
Question 14 |
Which of the following sorting algorithms has the lowest worst-case complexity?
Merge sort | |
Bubble Sort | |
Quick Sort | |
Selection Sort |
Merge sort→ O(nlogn)
Bubble sort→ O(n2)
Quick sort→ O(n2)
Selection sort→ O(n2)
Question 15 |
Consider the following segment of C-code:
int j, n;
j = 1;
while (j <= n)
j = j*2; The number of comparisons made in the execution of the loop for any n > 0 is: Base of Log is 2 in all options.
⌈log2n⌉ + 1
| |
n | |
⌈log2n⌉ | |
⌊log2n⌋ + 1 |
1<=6 (✔️)
2<=6 (✔️)
4<=6 (✔️)
8<=6 (❌)
4 comparisons required
Option A:
[log n]+1
[log 6]+1
3+1 = 4 (✔)
Option B:
n=6 (❌)
Option C:
[log n]
[log 6]=3 (❌)
Option D:
[log2n]+1
[log26]+1 = 2+1 = 3 (❌)
Question 16 |
Group 1 contains some CPU scheduling algorithms and Group 2 contains some applications. Match entries in Group 1 to entries in Group 2.
Group I Group II (P) Gang Scheduling (1) Guaranteed Scheduling (Q) Rate Monotonic Scheduling (2) Real-time Scheduling (R) Fair Share Scheduling (3) Thread Scheduling
P – 3 Q – 2 R – 1 | |
P – 1 Q – 2 R – 3 | |
P – 2 Q – 3 R – 1 | |
P – 1 Q – 3 R – 2 |
⇒ Rate monotonic scheduling is used in Real-time operating system.
⇒ Fair share scheduling distributes the CPU equally among users due to which it generates scheduling process.
Question 17 |
Consider the following statements about user level threads and kernel level threads. Which one of the following statements is FALSE?
Context switch time is longer for kernel level threads than for user level threads. | |
User level threads do not need any hardware support.
| |
Related kernel level threads can be scheduled on different processors in a multi-processor system. | |
Blocking one kernel level thread blocks all related threads. |
B) True, because kernel is not involved in it.
C) True
D) Blocking one kernel level thread blocks all related threads is false, because kernel level threads are independent.
Question 18 |
Which one of the following is a top-down parser?
Recursive descent parser. | |
Operator precedence parser. | |
An LR(k) parser.
| |
An LALR(k) parser. |
Question 19 |
In Ethernet when Manchester encoding is used, the bit rate is:
Half the baud rate.
| |
Twice the baud rate. | |
Same as the baud rate. | |
None of the above. |
Question 20 |
Which one of the following uses UDP as the transport protocol?
HTTP | |
Telnet | |
DNS | |
SMTP |
HTTP, Telnet and SMTP uses TCP.
Question 21 |
How many different non-isomorphic Abelian groups of order 4 are there?
2 | |
3 | |
4 | |
5 |
4 = 22
So, prime no. is 2 and power of 2 is 2. So exponent value 2 is considered now.
Now the no. of ways we can divide 2 into sets will be the answer.
So division can be done as,
{1,1}, {0,2}
in two ways. Hence, answer is 2.
