GATE 2021 CS-Set-1
Question 1 |
Consider the following sentences:
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
(i) is grammatically incorrect and (ii) is ambiguous | |
(i) is grammatically correct and (ii) is ambiguous | |
(i) is grammatically correct and (ii) is unambiguous | |
(i) is grammatically incorrect and (ii) is unambiguous |
Question 1 Explanation:
i) Everybody in the class is prepared for the exam
This is grammatically correct statement
ii). Babu invited Danish to his home because he enjoys playing chess.
This statement is ambiguous as there is no guarantee that Danish knows playing chess.
ii). Babu invited Danish to his home because he enjoys playing chess.
This statement is ambiguous as there is no guarantee that Danish knows playing chess.
Question 2 |
| Items | Cost (₹) | Profit % | Marked Price (₹) |
| P | 5,400 | --- | 5,860 |
| Q | --- | 25 | 10,000 |
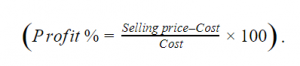
The discount on item Q, as a percentage of its marked price, is ______.
25 | |
5 | |
10 | |
12.5 |
Question 2 Explanation:
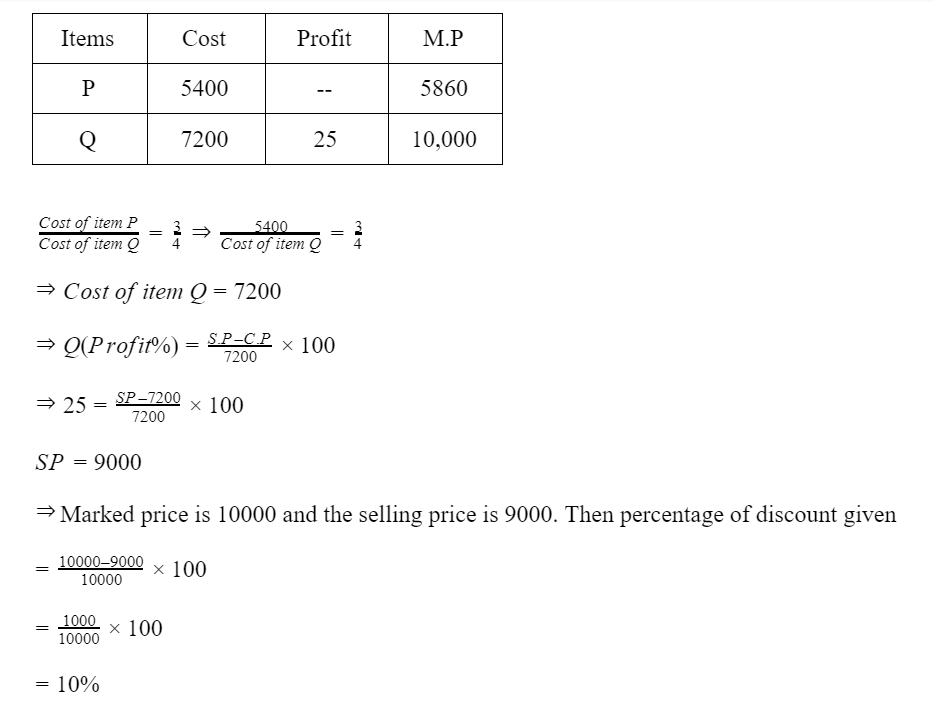
Question 3 |
The ratio of boys to girls in a class is 7 to 3.
Among the options below, an acceptable value for the total number of students in the class is:
37 | |
73 | |
21 | |
50 |
Question 3 Explanation:
The Ratio of boys to girls is 7:3
Number of boys = 7x
Number of girls = 3x
Total number of students = 10x
So the possible value should multiple by 10.
Answer is 50.
Number of boys = 7x
Number of girls = 3x
Total number of students = 10x
So the possible value should multiple by 10.
Answer is 50.
Question 4 |
A polygon is convex if, for every pair of points, P and Q belonging to the polygon, the line segment PQ lies completely inside or on the polygon.
Which one of the following is NOT a convex polygon?
Which one of the following is NOT a convex polygon?
 | |
 | |
 | |
 |
Question 4 Explanation:
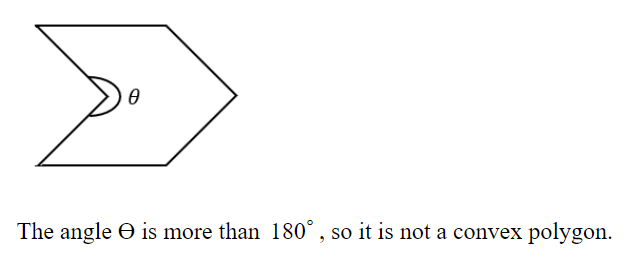
Question 5 |
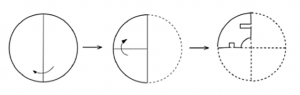
A circular sheet of paper is folded along the lines in the directions shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like _______.
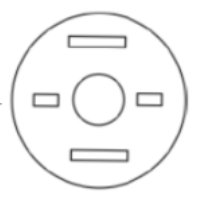 | |
 | |
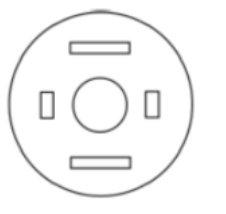 | |
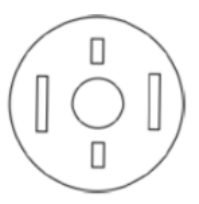 |
Question 5 Explanation:

Question 6 |
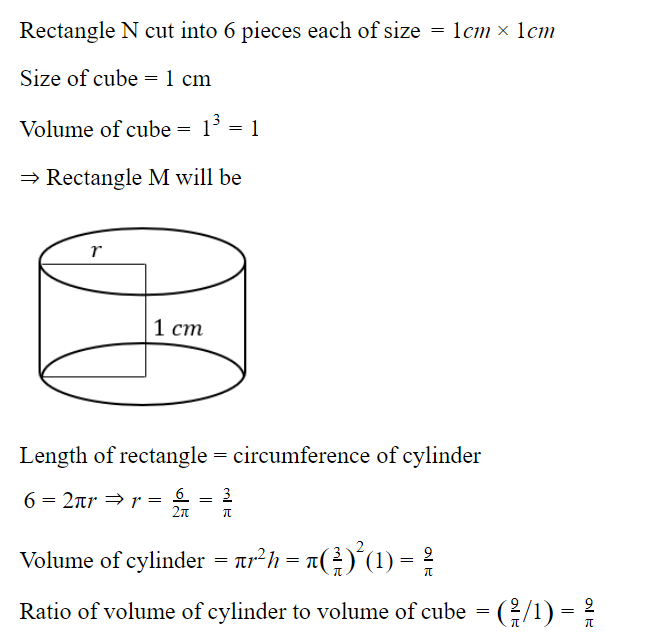
We have 2 rectangular sheets of paper, M and N, of dimensions 6 cm × 1 cm each. Sheet M is rolled to form an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal square patches and assembled to form the largest possible closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that of the cube is ______.
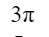 | |
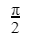 | |
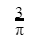 | |
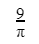 |
Question 6 Explanation:
Question 7 |
______ is to surgery as writer is to ______
Which one of the following options maintains a similar logical relation in the above sentence?
Which one of the following options maintains a similar logical relation in the above sentence?
Hospital, library | |
Medicine, grammar | |
Plan, outline | |
Doctor, book |
Question 7 Explanation:
The given statement is to fill the relationship of the subject and the action done by the subject.
Doctor is to surgery as writer is to book.
Doctor is to surgery as writer is to book.
Question 8 |
There are five bags each containing identical sets of ten distinct chocolates. One chocolate is picked from each bag.
The probability that at least two chocolates are identical is _____
0.81225 | |
0.4235 | |
0.6976 | |
0.3024 |
Question 8 Explanation:
Explanation :
There are 5 bags having identical sets of 10 distinct chocolates. one chocolate is drawn from each bag, probability to find at least 2 chocolate is identical
The total number of such selections possible = 10*10*10*10*10 = 10^5.
We need to select such that at least two of them are identical.
We can count the number of ways with no chocolate being repeated and subtract it from total possible ways to get the required probability.
The number of ways to select all different/distinct = 10*9*8*7*6
Required number of selections= 10^5-10*9*8*7*6 = 69760
Required probability = 69760/10^5 = 0.69760
There are 5 bags having identical sets of 10 distinct chocolates. one chocolate is drawn from each bag, probability to find at least 2 chocolate is identical
The total number of such selections possible = 10*10*10*10*10 = 10^5.
We need to select such that at least two of them are identical.
We can count the number of ways with no chocolate being repeated and subtract it from total possible ways to get the required probability.
The number of ways to select all different/distinct = 10*9*8*7*6
Required number of selections= 10^5-10*9*8*7*6 = 69760
Required probability = 69760/10^5 = 0.69760
Question 9 |
Some people suggest anti-obesity measures (AOM) such as displaying calorie information in restaurant menus. Such measures sidestep addressing the core problems that cause obesity: poverty and income inequality.
Which one of the following statements summarizes the passage?
Which one of the following statements summarizes the passage?
AOM are addressing the problem superficially. | |
The proposed AOM addresses the core problems that cause obesity. | |
AOM are addressing the core problems and are likely to succeed. | |
If obesity reduces, poverty will naturally reduce, since obesity causes poverty. |
Question 9 Explanation:
The problems mentioned are poverty and income inequality. But AOMs are not addressing the main problems directly. But it is a kind of generic step taken to address obesity. So AOMs are only addressing the obesity problem superficially but not addressing the real problems.
Question 10 |
Given below are two statements 1 and 2, and two conclusions I and II.
Statement I: All bacteria are microorganisms.
Statement II: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
Based on the above statements and conclusions, which one of the following options is logically CORRECT?
Statement I: All bacteria are microorganisms.
Statement II: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
Based on the above statements and conclusions, which one of the following options is logically CORRECT?
Only conclusion I is correct | |
Only conclusion II is correct | |
Neither conclusion I nor II is correct | |
Either conclusion I or II is correct |
Question 11 |
Consider the following ANSI C function:
int SimpleFunction (int Y[], int n, int x)
{
int total = Y[0], loopIndex;
for (loopIndex = 1; loopIndex <= n - 1; loopIndex++)
total = x * total + Y[loopIndex]
return total;
}
Let Z be an array of 10 elements with Z[i]=1, for all i such that 0 ≤ i ≤ 9. The value returned by SimpleFunction(Z, 10, 2) is _______
int SimpleFunction (int Y[], int n, int x)
{
int total = Y[0], loopIndex;
for (loopIndex = 1; loopIndex <= n - 1; loopIndex++)
total = x * total + Y[loopIndex]
return total;
}
Let Z be an array of 10 elements with Z[i]=1, for all i such that 0 ≤ i ≤ 9. The value returned by SimpleFunction(Z, 10, 2) is _______
1023 |
Question 11 Explanation:
Array Z consists of 10 elements and that element's values are 1.
n=10,x=2
Initial total value is 1 => total=1.
For loop will execute 9 times.
loopindex=1, 1<=9 condition is true then
total = x * total + Y[loopIndex]= 2*1+Y[1]=2+1=3
loopindex=2, 2<=9 condition is true then
total=2*3+Y[2]=6+1=7
loopindex=3, 3<=9 condition is true then
total=2*7+Y[3]=14+1 =15
loopindex=4, 4<=9 condition is true then
total= 2*15+Y[4]=30+1=31
loopindex=5, 5<=9 condition is true then
total=2*31+Y[5]=62+1=63
loopindex=6, 6<=9 condition is true then
total=2*63+Y[6]=126+1=127
loopindex=7, 7<=9 condition is true then
Total =2*127+Y[7]=254+1=255
loopindex=8, 8<=9 condition is true then
total=2*255+Y[8]=510+1=511
loopindex=9, 9<=9 condition is true then
total=2*511+Y[9]=1022+1=1023
loopindex=10, 10<=9 condition is false then
Total value is returned which is 1023.
You can also write generalized formulae 210-1=1023
n=10,x=2
Initial total value is 1 => total=1.
For loop will execute 9 times.
loopindex=1, 1<=9 condition is true then
total = x * total + Y[loopIndex]= 2*1+Y[1]=2+1=3
loopindex=2, 2<=9 condition is true then
total=2*3+Y[2]=6+1=7
loopindex=3, 3<=9 condition is true then
total=2*7+Y[3]=14+1 =15
loopindex=4, 4<=9 condition is true then
total= 2*15+Y[4]=30+1=31
loopindex=5, 5<=9 condition is true then
total=2*31+Y[5]=62+1=63
loopindex=6, 6<=9 condition is true then
total=2*63+Y[6]=126+1=127
loopindex=7, 7<=9 condition is true then
Total =2*127+Y[7]=254+1=255
loopindex=8, 8<=9 condition is true then
total=2*255+Y[8]=510+1=511
loopindex=9, 9<=9 condition is true then
total=2*511+Y[9]=1022+1=1023
loopindex=10, 10<=9 condition is false then
Total value is returned which is 1023.
You can also write generalized formulae 210-1=1023
Question 12 |
The following relation records the age of 500 employees of a company, where empNo (indicating the employee number) is the key:
empAge (empNo, age)
Consider the following relational algebra expression:

What does the above expression generate?

What does the above expression generate?
Employee numbers of all employees whose age is not the maximum. | |
Employee numbers of only those employees whose age is the maximum. | |
Employee numbers of all employees whose age is not the minimum. | |
Employee numbers of only those employees whose age is more than the age of exactly one other employee. |
Question 12 Explanation:
The given relational algebra expression will result in employees whose age is not minimum. The
given conditional join, joins the relations if the age is greater than any of the ages mentioned in the database.
Question 13 |
A TCP server application is programmed to listen on port number P on host S. A TCP client is connected to the TCP server over the network.
Consider that while the TCP connection was active, the server machine S crashed and rebooted. Assume that the client does not use the TCP keepalive timer.
Which of the following behaviours is/are possible?
If the client was waiting to receive a packet, it may wait indefinitely. | |
If the client sends a packet after the server reboot, it will receive a RST segment. | |
The TCP server application on S can listen on P after reboot. | |
If the client sends a packet after the server reboot, it will receive a FIN segment. |
Question 13 Explanation:
- True
Since broken connections can only be detected by sending data, the receiving side will wait forever. This scenario is called a “half-open connection” because one side realizes the connection was lost but the other side believes it is still active. - True
The situation resolves itself when client tries to send data to server over the dead connection, and server replies with an RST packet (not FIN). - True
Yes, a TCP Server can listen to the same port number even after reboot. For example, the SMTP service application usually listens on TCP port 25 for incoming requests. So, even after reboot the port 25 is assigned to SMTP. - False
The situation resolves itself when client tries to send data to server over the dead connection, and server replies with an RST packet (not FIN), causing client to finally to close the connection forcibly.
FIN is used to close TCP connections gracefully in each direction (normal close of connection), while TCP RST is used in a scenario where TCP connections cannot recover from errors and the connection needs to reset forcibly.
Question 14 |
Consider the following C code segment:
a = b + c;
e = a + 1;
d = b + c;
f = d + 1;
g = e + f;
In a compiler, this code segment is represented internally as a directed acyclic graph (DAG). The number of nodes in the DAG is _______
a = b + c;
e = a + 1;
d = b + c;
f = d + 1;
g = e + f;
In a compiler, this code segment is represented internally as a directed acyclic graph (DAG). The number of nodes in the DAG is _______
6 |
Question 15 |
Consider the following expression.
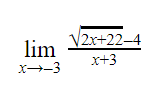
The value of the above expression (rounded to 2 decimal places) is _______
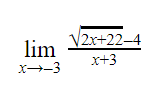
The value of the above expression (rounded to 2 decimal places) is _______
0.25 |
Question 15 Explanation:

Question 16 |
Consider a dynamic hashing approach for 4-bit integer keys:
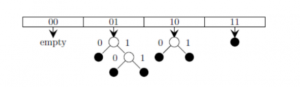
Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
- There is a main hash table of size 4.
- The 2 least significant bits of a key is used to index into the main hash table.
- Initially, the main hash table entries are empty.
- Thereafter, when more keys are hashed into it, to resolve collisions, the set of all keys corresponding to a main hash table entry is organized as a binary tree that grows on demand.
- First, the 3rd least significant bit is used to divide the keys into left and right subtrees.
- To resolve more collisions, each node of the binary tree is further sub-divided into left and right subtrees based on the 4th least significant bit.
- A split is done only if it is needed, i.e., only when there is a collison.

Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
10, 9, 6, 7, 5, 13 | |
9, 5, 13, 6, 10, 14 | |
9, 5, 10, 6, 7, 1 | |
5, 9, 4, 13, 10, 7 |
Question 16 Explanation:
The key insertions 10, 9, 6, 7, 5, 13 would result in the state of the given hash table.
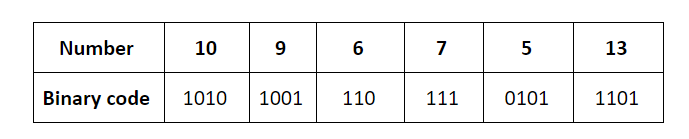
The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
![]()
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.

The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.
There are 16 questions to complete.
