Engineering-Mathematics
Question 1 |
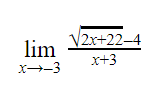
The value of the above expression (rounded to 2 decimal places) is _______
A | 0.25 |

Question 2 |

Which one of the following choices is correct?
A | Both S1and S2 are tautologies. |
B | Neither S1and S2 are tautology. |
C | S1is not a tautology but S2is a tautology. |
D | S1is a tautology but S2is not a tautology. |
A tautology is a formula which is "always true" . That is, it is true for every assignment of truth values to its simple components.
Method 1:
S1: (~p ^ (p Vq)) →q
The implication is false only for T->F condition.
Let's consider q as false, then
(~p ^ (p Vq)) will be (~p ^ (p VF)) = (~p ^ (p)) =F.
It is always F->F which is true for implication. So there are no cases that return false, thus its always True i.e. its Tautology.
S2:
q->(~p (p Vq))
The false case for implication occurs at T->F case.
Let q=T then (~p (p Vq)) = (~p (p VT))= ~p. (It can be false for p=T).
So there is a case which yields T->F = F. Thus its not Valid or Not a Tautology.
Method 2:

Question 3 |
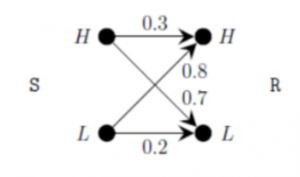
If the received signal is H, the probability that the transmitted signal was H (rounded to 2 decimal places) is _______
A | 0.04 |
Bayes theorem:
Probability of event A happening given that event B has already happened is
P(A/B) = P(B/A)*P(A) / P(B)
Here, it is asked that P( H transmitted / H received).
S can send signal to H with 0.1 probability, S can send signal to L with 0.9 probability.
The complete diagram can be
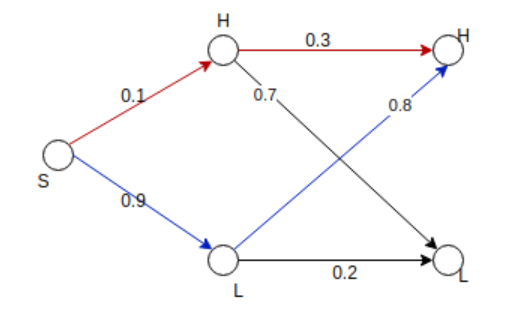
Probability that H Transmitted (H_t) given that H received (H_r)is
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
P(H-r) = probability that H received = P( H received from H)+ P(H received from L)
It can be observed from the graph that H can receive in two ways (S to H to H) and (S to L to H)
The P(H_r) = 0.1*0.3 + 0.9*0.8= 0.03+0.72 = 0.75
P(H_received given that H_transmitted) =0.3
P(H transmitted ) = 0.1 i.e.
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
= 0.3*0.1 / 0.75 = 0.04
Question 4 |
A | 11 |
v - e + f = 2
v is number of vertices
e is number of edges
f is number of faces including bounded and unbounded
8-e+5=2
=> 13-2 =e
The number of edges are =11
Question 5 |
S1: There exist random variables X and Y such that
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
S2: For all random variables X and Y,
CovX,Y=E|X-E[X]| |Y-E[Y]|
Which one of the following choices is correct?
A | S1is false, but S2is true. |
B | Both S1and S2are true. |
C | S1is true, but S2is false. |
D | Both S1and S2 are false. |
For a dataset with single values, we have variance 0. EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
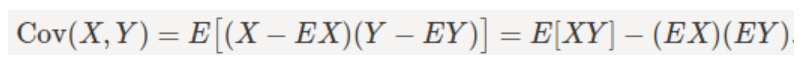
Its not |x-E(x)|. Thus S2 is also incorrect.
Question 6 |
Which one of the following options is correct?
A | G is always cyclic, but H may not be cyclic. |
B | Both G and H are always cyclic. |
C | G may not be cyclic, but H is always cyclic. |
D | Both G and H may not be cyclic. |
If ‘G’ is a group with sides 6, its subgroups can have orders 1, 2, 3, 6.
(The subgroup order must divide the order of the group)
Given ‘H’ can be 1 to 6, but 4, 5 cannot divide ‘6’.
Then ‘H’ is not a subgroup.
G can be cyclic only if it is abelian. Thus G may or may not be cyclic.
The H can be cyclic only for the divisors of 6 and H cannot be cyclic for any non divisors of 6.
Question 7 |
A | If a relation S is reflexive and circular, then S is an equivalence relation. |
B | If a relation S is transitive and circular, then S is an equivalence relation. |
C | If a relation S is circular and symmetric, then S is an equivalence relation. |
D | If a relation S is reflexive and symmetric, then S is an equivalence relation. |
Theorem: A relation R on a set A is an equivalence relation if and only if it is reflexive and circular.
For symmetry, assume that x, y ∈ A so that xRy, lets check for yRx.
Since R is reflexive and y ∈ A, we know that yRy. Since R is circular and xRy and yRy, we know that yRx. Thus R is symmetric.
For transitivity, assume that x, y, z ∈ A so that xRy and yRz. Check for xRz. Since R is circular and xRy and yRz, we know that zRx. Since we already proved that R is symmetric, zRx implies that xRz. Thus R is transitive.
Question 8 |
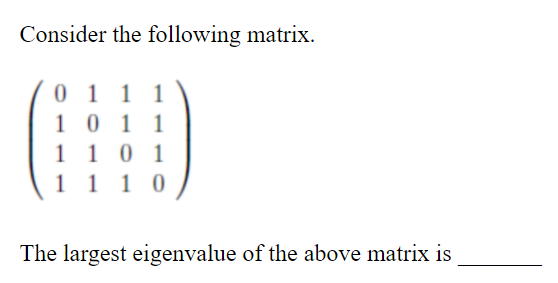
A | 3 |

Question 9 |
A | 0.37 |

Question 10 |

Let M be the adjacency matrix of G.
Define graph G2on the same set of vertices with adjacency matrix N, where

Which one of the following statements is true?
A | 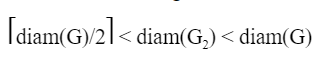 |
B | 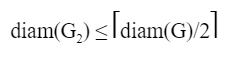 |
C |  |
D | 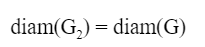 |



Question 11 |
The eigen vector(s) of the matrix
is (are)
A | (0,0,α ) |
B | (α,0,0) |
C | (0,0,1) |
D | (0,α,0) |
E | Both B and D |
So the question as has
(A - λI)X = 0
AX = 0
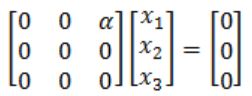
What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
Question 12 |
The differential equation
d2y/dx2 + dy/dx + siny = 0 is:
A | linear |
B | non-linear |
C | homogeneous |
D | of degree two |
d2y/dx2 + dy/dx + siny = 0
In this DE, degree is 1 then this represent linear equation.
Question 13 |
Simpson’s rule for integration gives exact result when f(x) is a polynomial of degree
A | 1 |
B | 2 |
C | 3 |
D | 4 |
Question 14 |
Fourier series of the periodic function (period 2π) defined by

But putting x = π, we get the sum of the series.
A | π2/4 |
B | π2/6 |
C | π2/8 |
D | π2/12 |
Question 15 |
Which of the following improper integrals is (are) convergent?
A | 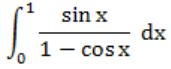 |
B | 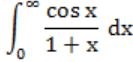 |
C |  |
D |  |
Question 16 |
The function f(x,y) = x2y - 3xy + 2y + x has
A | no local extremum |
B | one local minimum but no local maximum |
C | one local maximum but no local minimum |
D | one local minimum and one local maximum |
Question 17 |
A | 1 |
Question 18 |
The radius of convergence of the power series
A | Out of syllabus. |
Question 19 |
If the linear velocity ![]() is given by
is given by
The angular velocity ![]() at the point (1, 1, -1) is ________
at the point (1, 1, -1) is ________
A | Out of syllabus. |
Question 20 |
Given the differential equation, y′ = x − y with the initial condition y(0) = 0. The value of y(0.1) calculated numerically upto the third place of decimal by the second order Runga-Kutta method with step size h = 0.1 is ________
A | Out of syllabus. |
Question 21 |
For X = 4.0, the value of I in the FORTRAN 77 statement
1 = -2**2 + 5.0*X/X*3 + 3/4 is _______
A | Out of syllabus. |
Question 22 |
The value of the double integral ![]() is
is
A | 1/3 |
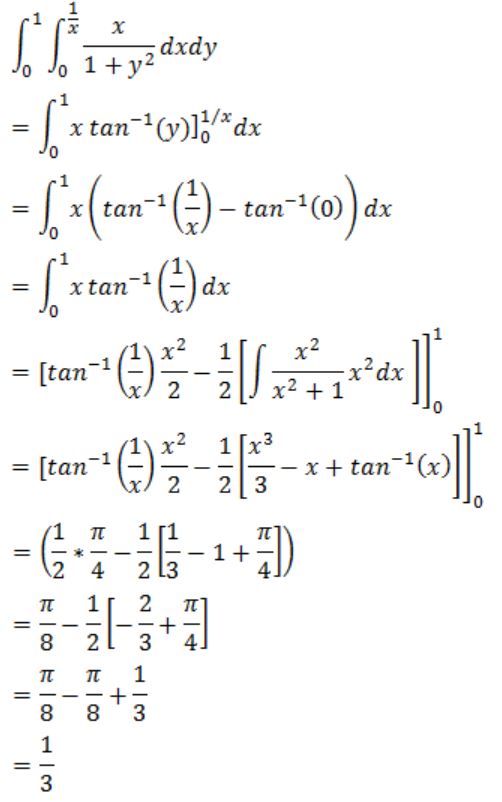
Question 23 |
If  the matrix A4, calculated by the use of Cayley-Hamilton theorem or otherwise, is _________
the matrix A4, calculated by the use of Cayley-Hamilton theorem or otherwise, is _________
A | A4 = I |
(1-λ) (-1-λ) (i-λ) (-i-λ)
= (λ2-1) (λ2+1)
= λ4-1
Characteristic equation is λ4-1 = 0.
According to Cayley-Hamilton theorem, every matrix satisfies its own characteristic equation, so
A4 = I
Question 24 |
Given ![]() and S the surface of a unit cube with one corner at the origin and edges parallel to the coordinate axes, the value of integral
and S the surface of a unit cube with one corner at the origin and edges parallel to the coordinate axes, the value of integral
A | Out of syllabus. |
Question 25 |
The differential equation yn + y = 0 is subjected to the boundary conditions.
y (0) = 0 y(λ) = 0
In order that the equation has non-trivial solution(s), the general value of λ is __________
A | Out of syllabus. |
Question 26 |
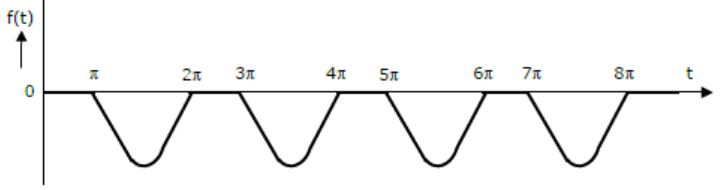
The Laplace transform of the periodic function f(t) described by the curve below, i.e.,
is _________
A | Out of syllabus. |
Question 27 |
The proposition p ∧(~p ∨ q) is:
A | a tautology |
B | logically equivalent to p ∧ q |
C | logically equivalent to p ∨ q |
D | a contradiction |
E | none of the above |
(p ∧ ~p) ∨ (p ∧ q)
F ∨ (p ∧ q)
(p ∧ q)
Question 28 |
Let S be an infinite set and S1 ..., Sn be sets such that S1 ∪ S2 ∪ ... ∪ Sn = S. Then,
A | at least one of the set Si is a finite set |
B | not more than one of the set Si can be finite |
C | at least one of the sets Si is an infinite set |
D | not more than one of the sets Si can be infinite |
E | None of the above |
Question 29 |
Let A be a finite set of size n. The number of elements in the power set of A × A is:
A | 22n |
B | 2n2 |
C | (2n)2 |
D | (22)n |
E | None of the above |
A = {1,2}
|A| = {∅, {1}, {2}, {1,2}}
Cardinality of power set of A = 2n2
A × A = {1,2} × {1,2}
= {(1,1), (1,2), (2,1), (2,2)}
Cardinality of A × A = n2
Cardinality of power set of A × A = 2n2
Question 30 |
The less-than relation, <, on reals is
A | a partial ordering since it is asymmetric and reflexive |
B | a partial ordering since it is antisymmetric and reflexive |
C | not a partial ordering because it is not asymmetric and not reflexive |
D | not a partial ordering because it is not antisymmetric and reflexive
|
E | none of the above |
1) not reflexive
2) irreflexive
3) not symmetric
4) Asymmetric
5) Antisymmetric
Question 31 |
Let A and B be sets with cardinalities m and n respectively. The number of one-one mappings (injections) from A to B, when m < n, is:
A | mn |
B | nPm |
C | mCn |
D | nCm |
E | mPn |
A = {a1, a2, ... am} and
B = {b1, b2, ... bn}
A one-one function 'f' assigns each element ai of A a distinct element, bj=f(ai) of Bi for a, there are n choices, for a2 there are n-1 choices, for am there are (n-(m-1)) choices.
i.e.,

Question 32 |
Show that proposition C is a logical consequence of the formula
A ∧ (A →(B ∨ C)) ∧ (B → ~A)
Using truth tables.
A | Theory Explanation. |
Question 33 |
Let ({p,q{,*) be a semigroup where p * q = q. Show that:
(a) p * q = q * p and (b) q * q = q
A | Theory Explanation. |
Question 34 |
Let A and B be real symmetric matrices of size n × n. Then which one of the following is true?
A | AA′ = 1 |
B | A = A-1 |
C | AB = BA |
D | (AB)' = BA |

Question 35 |
Backward Euler method for solving the differential equation dy/dx = f(x,y) is specified by, (choose one of the following).
A | yn+1 = yn + hf(xn, yn) |
B | yn+1 = yn + hf(xn+1, yn+1) |
C | yn+1 = yn-1 + 2hf(xn, yn) |
D | yn+1 = (1 + h) f(xn+1, yn+1) |
With initial value y(x0) = y0. Here the function f and the initial data x0 and y0 are known. The function y depends on the real variable x and is unknown. A numerical method produces a sequence y0, y1, y2, ....... such that yn approximates y(x0 + nh) where h is called the step size.
→ The backward Euler method is helpful to compute the approximations i.e.,
yn+1 = yn + hf(x n+1, yn+1)
Question 36 |
Let A and B be any two arbitrary events, then, which one of the following is true?
A | P(A∩B) = P(A)P(B) |
B | P(A∪B) = P(A) + P(B) |
C | P(A|B) = P(A∩B)P(B) |
D | P(A∪B) ≤ P(A) + P(B) |
(B) Happens when A and B are mutually exclusive.
(C) Not happens.
(D) P(A∪B) ≤ P(A) + P(B) is true because P(A∪B) = P(A) + P(B) - P(A∩B).
Question 37 |
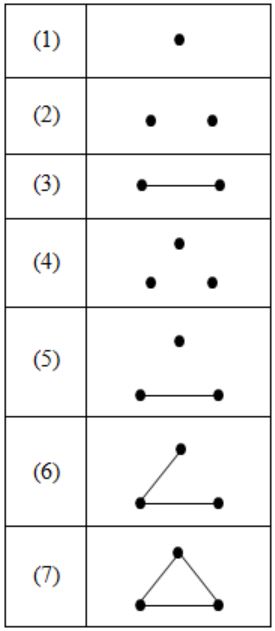
The number of distinct simple graphs with upto three nodes is
A | 15 |
B | 10 |
C | 7 |
D | 9 |
Question 38 |
The tank of matrix ![]() is:
is:
A | 0 |
B | 1 |
C | 2 |
D | 3 |

Question 39 |
Some group (G,o) is known to be abelian. Then, which one of the following is true for G?
A | g = g-1 for every g ∈ G |
B | g = g2 for every g ∈ G |
C | (goh)2 = g2oh2 for every g,h ∈ G |
D | G is of finite order |
For Abelian group, commutative also holds
i.e., (aob) = (boa)
Consider option (C):
(goh)2 = (goh)o(gog)
= (hog)o(goh)
= (ho(gog)oh)
= ((hog2)oh)
= (g2oh)oh
= g2o(hoh)
= g2oh2 [True]
Question 40 |
In a compact single dimensional array representation for lower triangular matrices (i.e all the elements above the diagonal are zero) of size n × n, non-zero elements (i.e elements of the lower triangle) of each row are stored one after another, starting from the first row, the index of the (i, j)th element of the lower triangular matrix in this new representation is:
A | i + j |
B | i + j - 1 |
C | j + i(i-1)/2 |
D | i + j(j-1)/2 |
If we assume array index starting from 1 then, ith row contains i number of non-zero elements. Before ith row there are (i-1) rows, (1 to i-1) and in total these rows has 1+2+3......+(i-1) = i(i-1)/2 elements.
Now at ith row, the jth element will be at j position.
So the index of (i, j)th element of lower triangular matrix in this new representation is
j = i(i-1)/2
Question 41 |
The number of substrings (of all lengths inclusive) that can be formed from a character string of length n is
A | n |
B | n2 |
C | n(n-1)/2 |
D | n(n+1)/2 |
n = 1
(n-1) = 2
(n-2) = 3
So, Total = n(n+1)/2
Question 42 |
On the set N of non-negative integers, the binary operation __________ is associative and non-commutative.
A | fog |
(fog)(x) = f(g(x))
It is associative, (fog)oh = fo(goh), but its usually not commutative. fog is usually not equal to gof.
Note that if fog exists then gof might not even exists.
Question 43 |
Amongst the properties {reflexivity, symmetry, anti-symmetry, transitivity} the relation R = {(x,y) ∈ N2 | x ≠ y } satisfies __________.
A | symmetry |
It is symmetric as if xRy then yRx.
It is not antisymmetric as xRy and yRx are possible and we can have x≠y.
It is not transitive as if xRy and yRz then xRz need not be true. This is violated when x=x.
So, symmetry is the answer.
Question 44 |
The number of subsets {1, 2, ... n} with odd cardinality is __________.
A | 2n-1 |
And so, no. of subsets with odd cardinality is half of total no. of subsets = 2n /n = 2n-1
Question 45 |
The number of edges in a regular graph of degree d and n vertices is _________.
A | d*n/2 |
d * n = 2 * |E|
∴ |E| = d*n/2
Question 46 |
The probability of an event B is P1. The probability that events A and B occur together is P2 while the probability that A and ![]() occur together is P3. The probability of the event A in terms of P1, P2 and P3 is __________.
occur together is P3. The probability of the event A in terms of P1, P2 and P3 is __________.
A | P2 + P3 |
P3 = P(A) - P2
P(A) = P2 + P3
Question 47 |
Let A, B and C be independent events which occur with probabilities 0.8, 0.5 and 0.3 respectively. The probability of occurrence of at least one of the event is __________
A | 0.93 |
Since all the events are independent, so we can write
P(A∪B∪C) = P(A) + P(B) + P(C) - P(A)P(B) - P(B)P(C) - P(A)P(C) + P(A)P(B) P(C)
= 0.8 + 0.5 + 0.3 - 0.4 - 0.5 - 0.24 + 0.12
= 0.93
Question 48 |
The Hasse diagrams of all the lattices with up to four elements are __________ (write all the relevant Hasse diagrams).
A |  |
We can't draw lattice with 1 element.
For 2 element:

For 3 element:

For 4 element:

Question 49 |
Match the following items

A | (i) - (b), (ii) - (c), (iii) - (d), (iv) - (a) |
Question 50 |
Find the inverse of the matrix 
A | 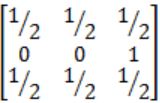 |
B | 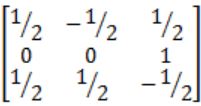 |
C |  |
D | 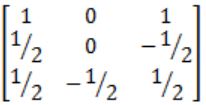 |
-λ3 + 2λ2 - 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 - 2I = 0
So, A-1 = 1/2 (2A - A2)
Solving we get,

