Theory-of-Computation
Question 1 |

A | 50 |


Question 2 |
L1=〈M〉|M takes more than 2021 steps on all inputs
L2=〈M〉|M takes more than 2021 steps on some input
Which one of the following options is correct?
A | Both L1and L2 are undecidable. |
B | L1is undecidable and L2is decidable. |
C | L1is decidable and L2is undecidable. |
D | Both L1and L2 are decidable. |
L1 is decidable.
We can take all strings of length zero to length 2021.
If TM takes more than 2021 steps on above inputs then definitely it will take more than 2021 steps on all input greater than length 2021.
If TM takes less than 2021 steps:
In such a case suppose TM takes less than 2021 steps (let's say 2020 steps ) for string length 2021, 2022, 2023, then definitely TM will take 2020 steps for all input greater than 2023. Hence in both cases it is decidable.
Similarly L2 is also decidable. If we can decide for all inputs then we can decide for some inputs also.
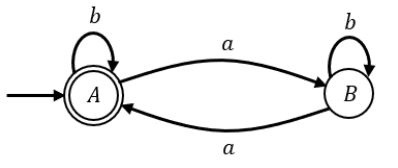
Question 3 |
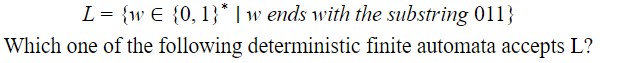
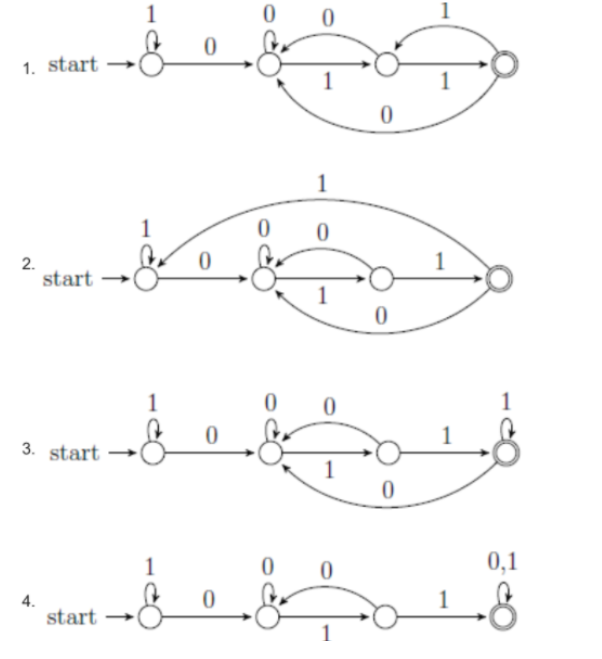
A | 2 |
Option A accepts string “01111” which does not end with 011 hence wrong.
Option C accepts string “0111” which does not end with 011 hence wrong.
Option D accepts string “0110” which does not end with 011 hence wrong.
Option B is correct.
The NFA for language in which all strings ends with “011”
Question 4 |
A | L = { |
B | L = { |
C | L = { |
D | L = { |

Question 5 |
A | L1. L2
|
B | L1 ∪ L2 |
C | L1 ∩ L2 |
D | L1 − L2 |
L1. L2 => regular . CFL == CFL. CFL (as every regular is CFL so we can assume regular as CFL)
Since CFL is closed under concatenation so
CFL. CFL= CFL
Hence
Regular . CFL = CFL is true
L1 ∪ L2 => Regular ∪ CFL = CFL
Regular ∪ CFL = CFL ∪ CFL (as every regular is CFL so we can assume regular as CFL)
Since CFL is closed under union
Hence Regular ∪ CFL = CFL is true
L1 ∩ L2 => Regular ∩ CFL = CFL
Regular languages are closed under intersection with any language
I.e,
Regular ∩ L = L (where L is any language such as CFL, CSL etc)
Hence Regular ∩ CFL = CFL is true
Please note this is a special property of regular languages so we will not upgrade regular into CFL (as we did in S1 and S2). We can directly use these closure properties.
L1 − L2 => Regular − CFL = CFL
=> Regular − CFL = regular ∩ CFL (complement)
Since CFL is not closed under complement so complement of CFL may or may not be CFL
Hence Regular − CFL need not be CFL
For ex:
R= (a+b+c)* and L= {am bn ck | m ≠ n or n ≠ k} which is CFL.
The complement of L = {an bn cn | n>0} which is CSL but not CFL.
So
R − L = (a+b+c)* − {am bn ck | m ≠ n or n ≠ k}
=> (a+b+c)* ∩ L (complement)
=> (a+b+c)* ∩ {an bn cn | n>0}
=> {an bn cn | n>0}
Which is CSL. Hence Regular − CFL need not be CFL.
Question 6 |
If the state machine described in figure, should have a stable state, the restriction on the inputs is given by

A | 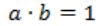 |
B | 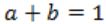 |
C |  |
D |  |
Question 7 |
A simple Pascal like language has only three statements.
(i) assignment statement e.g. x:=expression
(ii) loop construct e.g. for i:=expression to expression do statement.
(iii) sequencing e.g. begin statement ;…; statement end
(a) Write a context-free grammar (CFG) for statements in the above language. Assume that expression has already been defined. Do not use optional
parentheses and * operator in CFG.
(b) Show the parse tree for the following statement:
for j:=2 to 10 do
begin x:=expr1;
y:=expr2
end A | Theory Explanation. |
Question 8 |
Draw the state transition of a deterministic finite state automaton which accepts all strings from the alphabet {a,b}, such that no string has 3 consecutive occurrences of the letter b.
A | Theory Explanation. |
Question 9 |
Which of the following conversions is not possible (algorithmically)?
A | Regular grammar to context free grammar |
B | Non-deterministic FSA to deterministic FSA |
C | Non-deterministic PDA to deterministic PDA |
D | Non-deterministic Turing machine to deterministic Turing machine |
Question 10 |
Which of the following features cannot be captured by context-free grammars?
A | Syntax of if-then-else statements |
B | Syntax of recursive procedures |
C | Whether a variable has been declared before its use |
D | Variable names of arbitrary length |
Syntactic rules not checking the meaningful things such as if a variable is declared before it use (or) not.
Like this, things are handled by semantic analysis phase.
Question 11 |
The regular expression for the language recognized by the finite state automaton of figure is __________
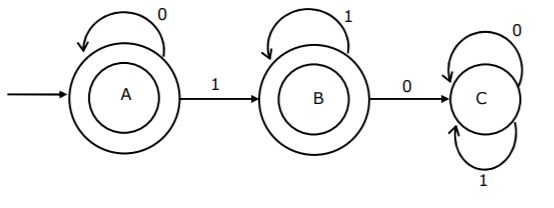
A | L = 0*1* |
L contains all binary strings where a 1 is not followed by a 0.
Question 12 |
Every subset of a countable set is countable.
State whether the above statement is true or false with reason.
A | True |
B | False |
Question 13 |
(a) Given a set
S = {x| there is an x-block of 5's in the decimal expansion of π}
(Note: x-block is a maximal block of x successive 5’s)
Which of the following statements is true with respect to S? No reasons need to be given for the answer.
- (i) S is regular
(ii) S is recursively enumerable
(iii) S is not recursively enumerable
(iv) S is recursive
(b) Given that a language L1 is regular and that the language L1 ∪ L2 is regular, is the language L2 always regular? Prove your answer.
A | Theory Explanation. |
Question 14 |
A grammar G is in Chomsky-Normal Form (CNF) if all its productions are of the form A → BC or A → a, where A, B and C, are non-terminals and a is a terminal. Suppose G is a CFG in CNF and w is a string in L(G) of length, then how long is a derivation of w in G?
A | Theory Explanation. |
Question 15 |
In some programming languages, an identifier is permitted to be a letter following by any number of letters or digits. If L and D denote the sets of letters and digits respectively, which of the following expressions defines an identifier?
A | (L ∪ D)+ |
B | L(L ∪ D)* |
C | (L⋅D)* |
D | L⋅(L⋅D)* |
L(L ∪ D)*
Question 16 |
Consider a grammar with the following productions
S → a∝b|b∝c| aB S → ∝S|b S → ∝b b|ab S ∝ → bd b|b
The above grammar is:
A | Context free |
B | Regular |
C | Context sensitive |
D | LR(k) |
Because LHS must be single non-terminal symbol.
S ∝→ b [violates CSG]
→ Length of RHS production must be atleast same as that of LHS.
Extra information is added to the state by redefining iteams to include a terminal symbol as second component in this type of grammar.
Ex: [A → αβa]
A → αβ is a production, a is a terminal (or) right end marker $, such an object is called LR(k).
So, answer is (D) i.e., LR(k).
Question 17 |
Which of the following definitions below generates the same language as L, where L = {xnyn such that n >= 1}?
I. E → xEy|xy II. xy|(x+xyy+) III. x+y+
A | I only |
B | I and II |
C | II and III |
D | II only |
Question 18 |
A finite state machine with the following state table has a single input x and a single out z.
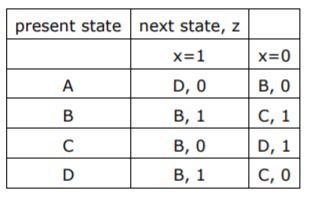
If the initial state is unknown, then the shortest input sequence to reach the final state C is:
A | 01 |
B | 10 |
C | 101 |
D | 110 |
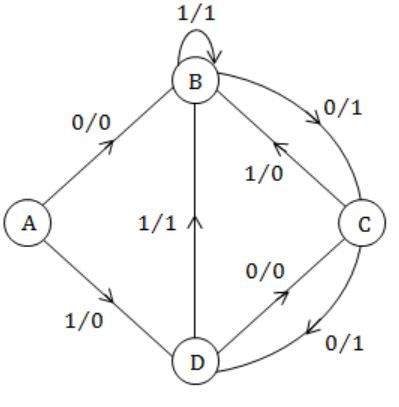
If A is the start state, shortest sequence is 10 'or' 00 to reach C.
If B is the start state, shortest sequence is 0 to reach C.
If C is the start state, shortest sequence is 10 or 00 to reach C.
If D is the start state, shortest sequence is 0 to reach C.
∴ (B) is correct.
Question 19 |
Let Σ = {0,1}, L = Σ* and R = {0n1n such that n >0} then the languages L ∪ R and R are respectively
A | regular, regular |
B | not regular, regular |
C | regular, not regular |
D | not regular, no regular |
Question 20 |
Let L be a language over ∑ i.e., *L ≤ ∑ . Suppose L satisfies the two conditions given below
(i) L is in NP and
(ii) For every n, there is exactly one string of length n that belongs to L.
Let Lc be the complement of L over ∑*. Show that Lc is also in NP.
A | Theory Explanation. |
Question 21 |
Consider the language L = {an| n≥0} ∪ {anbn| n≥0} and the following statements.
- I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
A | II only |
B | III only |
C | I only |
D | I and III only |
We can make DPDA for this.

L is not LL(k) for any “k” look aheads. The reason is the language is a union of two languages which have common prefixes. For example strings {aa, aabb, aaa, aaabbb,….} present in language. Hence the LL(k) parser cannot parse it by using any lookahead “k” symbols.
Question 22 |
Consider the following statements.
- I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
A | Both I and II
|
B | II only |
C | Neither I nor II |
D | I only
|
Assume L1 = {an bn | n>0} and L2 = complement of L1
L1 and L2 both are DCFL but not regular, but L1 U L2 = (a+b)* which is regular.
Hence even though L1 U L2 is regular, L1 and L2 need not be always regular.
Statement II is wrong.
Assume the following finite (hence regular) languages.
L1 = {ab}
L2 = {aabb}
L3 = {aaabbb}
.
.
.
L100 = {a100 b100}
.
.
.
If we take infinite union of all above languages i.e,
{L1 U L2 U ……….L100 U ……}
then we will get a new language L = {an bn | n>0}, which is not regular.
Hence regular languages are not closed under infinite UNION.
Question 23 |
Which one of the following regular expressions represents the set of all binary strings with an odd number of 1’s?
A | 10*(0*10*10*)*
|
B | ((0 + 1)*1(0 + 1)*1)*10*
|
C | (0*10*10*)*10* |
D | (0*10*10*)*0*1
|
The regular expression ((0+1)*1(0+1)*1)*10* generate string “11110” which is not having odd number of 1’s , hence wrong option.
The regular expression (0*10*10*)10* is not a generating string “01”. Hence this is also wrong . It seems none of them is correct.
NOTE: Option 3 is most appropriate option as it generates the max number of strings with odd 1’s.
But option 3 is not generating odd strings. So, still it is not completely correct.
The regular expression (0*10*10*)*0*1 always generates all string ends with “1” and thus does not generate string “01110” hence wrong option.
Question 24 |
Which of the following languages are undecidable? Note that
- L1 =
L2 = {
L3 = {
L4 = {
A | L2 and L3 only
|
B | L1 and L3 only
|
C | L2, L3 and L4 only |
D | L1, L3 and L4 only |
Only L3 is decidable. We can check whether a given TM reach state q in exactly 100 steps or not. Here we have to check only upto 100 steps, so here is not any case of going to infinite loop.
Question 25 |
Consider the following language.
L = {x ∈ {a,b}* | number of a’s in x is divisible by 2 but not divisible by 3}
The minimum number of states in a DFA that accepts L is ______.
A | 6 |
DFA 1: No. of a’s not divisible by 3
Using product automata:

Question 26 |
Consider the following languages.
- L1 = {wxyx | w,x,y ∈ (0 + 1)+}
L2 = {xy | x,y ∈ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
A | L1 is context-free but not regular and L2 is context-free. |
B | Neither L1 nor L2 is context-free.
|
C | L1 is regular and L2 is context-free.
|
D | L1 is context-free but L2 is not context-free. |
So it is equivalent to
(a+b)+ a (a+b)+ a + (a+b)+ b (a+b)+ b
L2 is CFL since it is equivalent to complement of L=ww.
Complement of L=ww is CFL.
Question 27 |
Which two of the following four regular expressions are equivalent? (ε is the empty string).
- (i) (00)*(ε+0)
(ii) (00)*
(iii) 0*
(iv) 0(00)*
A | (i) and (ii) |
B | (ii) and (iii) |
C | (i) and (iii) |
D | (iii) and (iv) |
In these two, we have any no. of 0's as well as null.
Question 28 |
Which of the following statements is false?
A | The Halting problem of Turing machines is undecidable. |
B | Determining whether a context-free grammar is ambiguous is undecidbale. |
C | Given two arbitrary context-free grammars G1 and G2 it is undecidable whether L(G1) = L(G2). |
D | Given two regular grammars G1 and G2 it is undecidable whether L(G1) = L(G2). |
1) Membership
2) Emtiness
3) Finiteness
4) Equivalence
5) Ambiguity
6) Regularity
7) Everything
8) Disjointness
All are decidable for Regular languages.
→ First 3 for CFL.
→ Only 1st for CSL and REC.
→ None for RE.
Question 29 |
Let L ⊆ Σ* where Σ = {a, b}. Which of the following is true?
A | L = {x|x has an equal number of a's and b's } is regular |
B | L = {anbn|n≥1} is regular |
C | L = {x|x has more a's and b's} is regular |
D | L = {ambn|m ≥ 1, n ≥ 1} is regular |
Here, m and n are independent.
So 'L' Is Regular.
Question 30 |
If L1 and L2 are context free languages and R a regular set, one of the languages below is not necessarily a context free language. Which one?
A | L1, L2 |
B | L1 ∩ L2 |
C | L1 ∩ R |
D | L1 ∪ L2 |
Question 31 |
Define for a context free language L ⊆ {0,1}*, init(L) = {u ∣ uv ∈ L for some v in {0,1}∗} (in other words, init(L) is the set of prefixes of L)
Let L = {w ∣ w is nonempty and has an equal number of 0’s and 1’s}
Then init(L) is
A | the set of all binary strings with unequal number of 0’s and 1’s |
B | the set of all binary strings including the null string |
C | the set of all binary strings with exactly one more 0’s than the number of 1’s or one more 1 than the number of 0’s |
D | None of the above |
Question 32 |
The grammar whose productions are
→ if id then → if id then else → id := id
is ambiguous because
A | the sentence if a then if b then c:=d |
B | the left most and right most derivations of the sentence if a then if b then c:=d give rise top different parse trees |
C | the sentence if a then if b then c:=d else c:=f has more than two parse trees |
D | the sentence if a then if then c:=d else c:=f has two parse trees |
"if a then if b then c:=d else c:=f".
Parse tree 1:

Parse tree 2:
Question 33 |
Consider the given figure of state table for a sequential machine. The number of states in the minimized machine will be
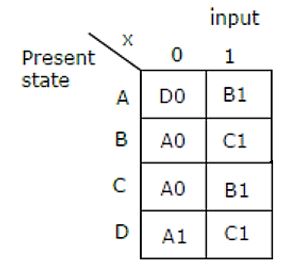
A | 4 |
B | 3 |
C | 2 |
D | 1 |
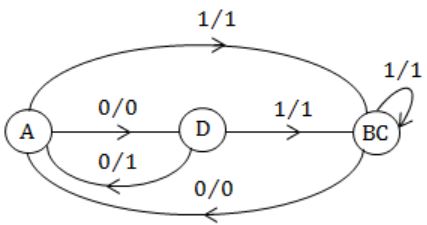
Question 34 |
Let G be a context-free grammar where G = ({S, A, B, C},{a,b,d},P,S) with the productions in P given below.
S → ABAC A → aA ∣ ε B → bB ∣ ε C → d
(ε denotes null string). Transform the grammar G to an equivalent context-free grammar G' that has no ε productions and no unit productions. (A unit production is of the form x → y, and x and y are non terminals.)
A | Theory Explanation. |
Question 35 |
Let Q = ({q1,q2}, {a,b}, {a,b,Z}, δ, Z, ϕ) be a pushdown automaton accepting by empty stack for the language which is the set of all non empty even palindromes over the set {a,b}. Below is an incomplete specification of the transitions δ. Complete the specification. The top of the stack is assumed to be at the right end of the string representing stack contents.
(1) δ(q1,a,Z) = {(q1,Za)}
(2) δ(q1,b,Z) = {(q1,Zb)}
(3) δ(q1,a,a) = {(.....,.....)}
(4) δ(q1,b,b) = {(.....,.....)}
(5) δ(q2,a,a) = {(q2,ϵ)}
(6) δ(q2,b,b) = {(q2,ϵ)}
(7) δ(q2,ϵ,Z) = {(q2,ϵ)} A | Theory Explanation. |
Question 36 |
If L is a regular language over Σ = {a,b}, which one of the following languages is NOT regular?
A | Suffix (L) = {y ∈ Σ* such that xy ∈ L} |
B | {wwR │w ∈ L} |
C | Prefix (L) = {x ∈ Σ*│∃y ∈ Σ* such that xy ∈ L} |
D | L ∙ LR = {xy │ x ∈ L, yR ∈ L} |
Question 37 |
For Σ = {a,b}, let us consider the regular language L = {x|x = a2+3k or x = b10+12k, k ≥ 0}. Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L?
A | 3 |
B | 9 |
C | 5 |
D | 24 |
For any language L, there exists an integer n, such that for all x ∈ L with |x| ≥ n, there exists u,v, w ∈ Σ*, such that x = uvw, and
(1) |uv| ≤ n
(2) |v| ≥ 1
(3) for all i ≥ 0: uviw ∈ L
We have to find "n" which satisfies for all the strings in L.
Considering strings derived by b10+12k.
The minimum string in L = "bbbbbbbbbb" but this string b10 cannot be broken in uvw.
So, pumping length 3, 9 and 5 cannot be the correct answer.
So, the minimum pumping length, such that any string in L can be divided into three parts "uvw" must be greater than 10.
Question 38 |
Consider the following sets:
- S1. Set of all recursively enumerable languages over the alphabet {0,1}
S2. Set of all syntactically valid C programs
S3. Set of all languages over the alphabet {0,1}
S4. Set of all non-regular languages over the alphabet {0,1}
Which of the above sets are uncountable?
A | S2 and S3 |
B | S3 and S4 |
C | S1 and S4 |
D | S1 and S2 |
S2 is countable, since a valid C program represents a valid algorithm and every algorithm corresponds to a Turing Machine, so S2 is equivalent to set of all Turing Machines.
S3 is is uncountable, it is proved by diagonalization method.
S4 is uncountable, as set of non-regular languages will have languages which is set of all languages over alphabet {0,1} i.e., S3.
Question 39 |
Which one of the following languages over Σ = {a,b} is NOT context-free?
A | {wwR |w ∈ {a,b}*} |
B | {wanwRbn |w ∈ {a,b}*, n ≥ 0} |
C | {anbi | i ∈ {n, 3n, 5n}, n ≥ 0} |
D | {wanbnwR |w ∈ {a,b}*, n ≥ 0} |
This is similar to language
L = {anbmcndm | n, m > 0}
Suppose we push “w” then an and then wR, now we cannot match bn with an, because in top of stack we have wR.
Question 40 |
Let Σ be the set of all bijections from {1, ..., 5} to {1, ..., 5}, where id denotes the identity function i.e. id(j) = j,∀j. Let º denote composition on functions. For a string x = x1 x2 ... xn ∈ Σn, n ≥ 0. Let π(x) = x1 º x2 º ... º xn.
Consider the language L = {x ∈ Σ* | π(x) = id}. The minimum number of states in any DFA accepting L is ______.
A | 120 |
B | 136 |
C | 125 |
D | 132 |
Question 41 |
Given Σ = {a,b}, which one of the following sets is not countable?
A | Set of all strings over Σ |
B | Set of all languages over Σ |
C | Set of all regular languages over Σ |
D | Set of all languages over Σ accepted by Turing machines |
Question 42 |
Which one of the following regular expressions over {0,1} denotes the set of all strings not containing 100 as a substring?
A | 0*(1+0)* |
B | 0*1010* |
C | 0*1*01 |
D | 0(10+1)* |
(B) generates 100 as substring.
(C) doesn't generate 1.
(D) answer.
Question 43 |
Which one of the following is not decidable?
A | Given a Turing machine M, a stings s and an integer k, M accepts s within k steps |
B | Equivalence of two given Turing machines |
C | Language accepted by a given finite state machine is not empty |
D | Language generated by a context free grammar is non empty |
In (A) the number of steps is restricted to a finite number 'k' and simulating a TM for 'k' steps is trivially decidable because we just go to step k and output the answer.
(B) Equivalence of two TM's is undecidable.
For options (C) and (D) we do have well defined algorithms making them decidable.
Question 44 |
Which of the following languages over {a,b,c} is accepted by a deterministic pushdown automata?
Note: wR is the string obtained by reversing 'w'.
A | {w⊂wR|w ∈ {a,b}*} |
B | {wwR|w ∈ {a,b,c}*} |
C | {anbncn|n ≥ 0} |
D | {w|w is a palindrome over {a,b,c}} |
(B) wwR, is realized by NPDA because we can't find deterministically the center of palindrome string.
(C) {anbncn | n ≥ 0} is CSL.
(D) {w | w is palindrome over {a,b,c}},
is realized by NPDA because we can't find deterministically the center of palindrome string.
Question 45 |
If the regular set A is represented by A = (01 + 1)* and the regular set ‘B’ is represented by B = ((01)*1*)*, which of the following is true?
A | A ⊂ B |
B | B ⊂ A |
C | A and B are incomparable |
D | A = B |
Question 46 |
Both A and B are equal, which generates strings over {0,1}, while 0 is followed by 1.
A | The numbers 1, 2, 4, 8, ……………., 2n, ………… written in binary |
B | The numbers 1, 2, 4, ………………., 2n, …………..written in unary |
C | The set of binary string in which the number of zeros is the same as the number of ones |
D | The set {1, 101, 11011, 1110111, ………..} |
10, 100, 1000, 10000 .... = 10*
which is regular and recognized by deterministic finite automata.
Question 47 |
Regarding the power of recognition of languages, which of the following statements is false?
A | The non-deterministic finite-state automata are equivalent to deterministic finite-state automata. |
B | Non-deterministic Push-down automata are equivalent to deterministic Push- down automata. |
C | Non-deterministic Turing machines are equivalent to deterministic Push-down automata. |
D | Both B and C |
C: Power (TM) > NPDA > DPDA.
Question 48 |
The string 1101 does not belong to the set represented by
A | 110*(0 + 1) |
B | 1 ( 0 + 1)* 101 |
C | (10)* (01)* (00 + 11)* |
D | Both C and D |
C & D are not generate string 1101.
Question 49 |
How many sub strings of different lengths (non-zero) can be found formed from a character string of length n?
A | n |
B | n2 |
C | 2n |
D |  |
Possible sub-strings are = {A, P, B, AP, PB, BA, APB}
Go through the options.
Option D:
n(n+1)/2 = 3(3+1)/2 = 6
Question 50 |
Let L be the set of all binary strings whose last two symbols are the same. The number of states in the minimum state deterministic finite 0 state automaton accepting L is
A | 2 |
B | 5 |
C | 8 |
D | 3 |

Equivalent DFA:
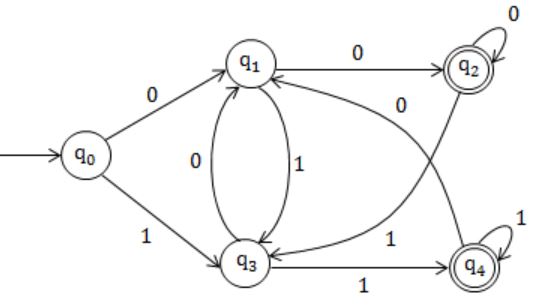
Hence, 5 states.
