UGC NET CS 2004 Dec-Paper-2
Question 1 |
AVA=A is called :
Identity law | |
De Morgan’ s law | |
Idempotent law | |
Complement law |
Question 1 Explanation:
→ De Morgan’s Laws:
(i). (A V B)’ = A' ∧ B'
(ii). (A ∧ B)’ = A' V B'
→ Identity Law :
(i). 1 AND A = A
(ii). 0 OR A = A
→ Complement law:
(i). A AND A'=1
(ii). A OR A'=0
→ Idempotent law:
The idempotence in the context of elements of algebras that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from idem + potence (same + power).
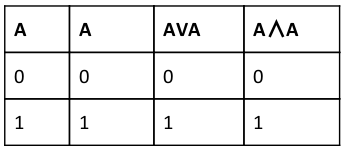
(i). A V A=A
(ii). A ∧ A=A
According to boolean algebra

(i). (A V B)’ = A' ∧ B'
(ii). (A ∧ B)’ = A' V B'
→ Identity Law :
(i). 1 AND A = A
(ii). 0 OR A = A
→ Complement law:
(i). A AND A'=1
(ii). A OR A'=0
→ Idempotent law:
The idempotence in the context of elements of algebras that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from idem + potence (same + power).
(i). A V A=A
(ii). A ∧ A=A
According to boolean algebra
Question 2 |
If f(x) = x+1 and g(x)=x+3 then f0 f0 f0 f is :
g | |
g+1 | |
g 4 | |
None of the above |
Question 2 Explanation:
Given data,
f(x)=x+1
g(x)=x+3
Constraint is f0 f0 f0 f
Step-1: We can write into fo fo fo f is f(f(f(x+1)))
We can write into f(f(x+2)) and f(x+3).
Step-2: Above constraint is equal to "x+4" because f(x+3)+1
Step-3: We can also write into fog(x)=x+4 and gof(x)=x+4.
So, g+1 is appropriate answer.
f(x)=x+1
g(x)=x+3
Constraint is f0 f0 f0 f
Step-1: We can write into fo fo fo f is f(f(f(x+1)))
We can write into f(f(x+2)) and f(x+3).
Step-2: Above constraint is equal to "x+4" because f(x+3)+1
Step-3: We can also write into fog(x)=x+4 and gof(x)=x+4.
So, g+1 is appropriate answer.
Question 3 |
The context-free languages are closed for :
(i) Intersection
(ii) Union
(iii) Complementation
(iv) Kleene Star
then
(i) Intersection
(ii) Union
(iii) Complementation
(iv) Kleene Star
then
(i) and (iv) | |
(i) and (iii) | |
(ii) and (iv) | |
(ii) and (iii) |
Question 3 Explanation:
The context free languages are closed under union and kleene star but it is not closed under intersection and complementation.
Note: Except intersection and complementation will closed under all operations in CFL.
Note: Except intersection and complementation will closed under all operations in CFL.
Question 4 |
The following lists are the degrees of all the vertices of a graph :
(i) 1, 2, 3, 4, 5
(ii) 3, 4, 5, 6, 7
(iii) 1, 4, 5, 8, 6
(iv) 3, 4, 5, 6
then
(i) 1, 2, 3, 4, 5
(ii) 3, 4, 5, 6, 7
(iii) 1, 4, 5, 8, 6
(iv) 3, 4, 5, 6
then
(i) and (ii) | |
(iii) and (iv) | |
(iii) and (ii) | |
(ii) and (iv) |
Question 4 Explanation:
Every graph is following basic 2 properties:
1. Sum of degrees of the vertices of a graph should be even.
2. Sum of degrees of the vertices of a graph is equal to twice the number of edges.
Statement-(i) is violating property-1.
= 1+2+3+4+5
= 15 is odd number.
Statement-(ii) is violating property-1.
= 3+4+5+6+7
= 25 is odd number.
Statement-(iii) is violating property-1.
= 1+4+5+8+6
= 24 is even number
Statement-(iv) is violating property-1
= 3+4+5+6
= 18 is even number
1. Sum of degrees of the vertices of a graph should be even.
2. Sum of degrees of the vertices of a graph is equal to twice the number of edges.
Statement-(i) is violating property-1.
= 1+2+3+4+5
= 15 is odd number.
Statement-(ii) is violating property-1.
= 3+4+5+6+7
= 25 is odd number.
Statement-(iii) is violating property-1.
= 1+4+5+8+6
= 24 is even number
Statement-(iv) is violating property-1
= 3+4+5+6
= 18 is even number
Question 5 |
If I m denotes the set of integers modulo m, then the following are fields with respect to the operations of addition modulo m and multiplication modulo m :
(i) Z 23
(ii) Z 29
(iii) Z 31
(iv) Z 33
Then
(i) Z 23
(ii) Z 29
(iii) Z 31
(iv) Z 33
Then
(i) only | |
(i) and (ii) only | |
(i), (ii) and (iii) only | |
(i), (ii), (iii) and (iv) |
Question 6 |
An example of a binary number which is equal to its 2 ’s complement is :
1100 | |
1001 | |
1000 | |
1111 |
Question 6 Explanation:
Option-A: 1100 convert into 2’s complement is
1100
1’s complement: 0011
2’s complement: 1
--------
0100
Option-B: 1001 convert into 2’s complement is
1001
1’s complement: 0110
2’s complement:
1
--------
0111
---------
Option-C: 1000 convert into 2’s complement is
1000
1’s complement: 0111
2’s complement:
1
--------
1000
---------
Option-D: 1111 convert into 2’s complement is
1111
1’s complement: 0000
2’s complement:
1
--------
0001
---------
So, Option-C is correct answer.
1100
1’s complement: 0011
2’s complement: 1
--------
0100
Option-B: 1001 convert into 2’s complement is
1001
1’s complement: 0110
2’s complement:
1
--------
0111
---------
Option-C: 1000 convert into 2’s complement is
1000
1’s complement: 0111
2’s complement:
1
--------
1000
---------
Option-D: 1111 convert into 2’s complement is
1111
1’s complement: 0000
2’s complement:
1
--------
0001
---------
So, Option-C is correct answer.
Question 7 |
When a tri - state logic device is in the third state, then :
it draws low current | |
it does not draw any current | |
it draws very high current | |
it presents a low impedance |
Question 7 Explanation:
Three Stage logic name itself implies there are 3 states of the buffer.
1. High (1)
2. Low (0)
3. High Impedance (Z)
→ High impedance means that a point in a circuit (a node) allows a relatively small amount of current through, per unit of applied voltage at that point.
→ High impedance circuits are low current, high voltage, whereas low impedance circuits are the opposite.
Truth table of Tri-state logic Inverter

1. High (1)
2. Low (0)
3. High Impedance (Z)
→ High impedance means that a point in a circuit (a node) allows a relatively small amount of current through, per unit of applied voltage at that point.
→ High impedance circuits are low current, high voltage, whereas low impedance circuits are the opposite.
Truth table of Tri-state logic Inverter

Question 8 |
An example of a connective which is not associative is :
AND | |
OR | |
EX-OR | |
NAND |
Question 8 Explanation:
→ OR is associative:
(i) (0 OR 1)OR 1
= 1 OR 1
= 1
(ii). 0 OR (1 OR 1)
= 0 OR 1
= 1
→ NAND is not associative
(i). (0 NAND 1)NAND 1
= 1 NAND 1
= 0
(ii). 0 NAND (1 NAND 1)
= 0 NAND 0
= 1
→ Ex-OR is associative
(i). (0 XOR 1) XOR 1
= 1 XOR 1
= 0
(ii). 0 XOR(1 XOR 1)
= 0 XOR 0
= 0
→ AND is associative:
(i) (0 AND 1) AND 1
= 0 AND 1
= 0
(ii). 0 AND (1 AND 1)
= 0 AND 1
= 0
(i) (0 OR 1)OR 1
= 1 OR 1
= 1
(ii). 0 OR (1 OR 1)
= 0 OR 1
= 1
→ NAND is not associative
(i). (0 NAND 1)NAND 1
= 1 NAND 1
= 0
(ii). 0 NAND (1 NAND 1)
= 0 NAND 0
= 1
→ Ex-OR is associative
(i). (0 XOR 1) XOR 1
= 1 XOR 1
= 0
(ii). 0 XOR(1 XOR 1)
= 0 XOR 0
= 0
→ AND is associative:
(i) (0 AND 1) AND 1
= 0 AND 1
= 0
(ii). 0 AND (1 AND 1)
= 0 AND 1
= 0
Question 9 |
Essential hazards may occur in :
Combinational logic circuits | |
Synchronous sequential logic circuits | |
Asynchronous sequential logic circuits working in the fundamental mode | |
Asynchronous sequential logic circuits working in the pulse mode |
Question 9 Explanation:
→ Essential hazards may occur in asynchronous sequential logic circuits working in the fundamental mode.
→ Asynchronous circuits is called essential hazard is caused by unequal delays along two or more paths that originate from the same same input.
→ It cannot be corrected by adding redundant gates and it can only be corrected by adjusting the amount of delay in the affected path.
→ Asynchronous circuits is called essential hazard is caused by unequal delays along two or more paths that originate from the same same input.
→ It cannot be corrected by adding redundant gates and it can only be corrected by adjusting the amount of delay in the affected path.
Question 10 |
The characteristic equation of a T flip-flop is:__[Note: The symbols used have the usual meaning]
Q n+1 = T ⊕ Q n | |
Q n+1 =T+Q n | |
Q n+1 =TQ n | |
Q n+1 = T Q n |
Question 10 Explanation:
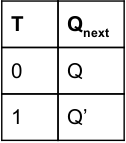
T-Flip flop Truth Table:

T-Flip-Flop Characteristic Table:

T-Flip-Flop Characteristic equation:
Q next = TQ' + T'Q

T-Flip-Flop Characteristic Table:
T-Flip-Flop Characteristic equation:
Q next = TQ' + T'Q
Question 11 |
Suppose x and y are two Integer Variables having values 0x5AB6 and 0x61CD respectively. The result (in hex) of applying bitwise operator and to x and y will be :
0 x 5089 | |
0 x 4084 | |
0 x 78A4 | |
0 x 3AD1 |
Question 11 Explanation:
Given two integer numbers are 0x5AB6 and 0x61CD
Step-1: Convert hexadecimal numbers into binary number because we want to perform AND operation.
0x5AB6 equivalent into binary number is 0101 1010 1011 0110
0x61CD equivalent into binary number is 0110 0001 1100 1101
Step-2: Perform Bitwise AND operation
0101 1010 1011 0110
0110 0001 1100 1101
-----------------------------
0100 0000 1000 0100(Bitwise AND operation)
------------------------------
Step-3: Convert result into hexadecimal number.
0100 0000 1000 0100 equivalent into hexadecimal number is 0x4084
Step-1: Convert hexadecimal numbers into binary number because we want to perform AND operation.
0x5AB6 equivalent into binary number is 0101 1010 1011 0110
0x61CD equivalent into binary number is 0110 0001 1100 1101
Step-2: Perform Bitwise AND operation
0101 1010 1011 0110
0110 0001 1100 1101
-----------------------------
0100 0000 1000 0100(Bitwise AND operation)
------------------------------
Step-3: Convert result into hexadecimal number.
0100 0000 1000 0100 equivalent into hexadecimal number is 0x4084
Question 12 |
Consider the following statements,
int i=4, j=3, k=0;
k= ++i- - -j + i++ - - - j +j++;
What will be the values of i, j and k after the statement.
int i=4, j=3, k=0;
k= ++i- - -j + i++ - - - j +j++;
What will be the values of i, j and k after the statement.
7, 2, 8 | |
5, 2, 10 | |
6, 2, 8 | |
4, 2, 8 |
Question 12 Explanation:
Given values are i=4, j=3 and k=0
Step-1: k= ++i- --j + i++ - --j +j++;
k= 5 - 2 + 5 - 1 + 1
k= (5-2)+(5-1)+1
= 3 + 4 + 1
= 8
Step-2: The value of i=6,j=2 and k=8
Step-1: k= ++i- --j + i++ - --j +j++;
k= 5 - 2 + 5 - 1 + 1
k= (5-2)+(5-1)+1
= 3 + 4 + 1
= 8
Step-2: The value of i=6,j=2 and k=8
There are 12 questions to complete.
