UGC NET CS 2006 Dec-paper-2
Question 1 |
Which of the regular expressions corresponds to this grammar ?
S →AB/AS, A→a/aA, B→b
S →AB/AS, A→a/aA, B→b
aa*b + | |
aa*b | |
(ab)* | |
a(ab)* |
Question 1 Explanation:
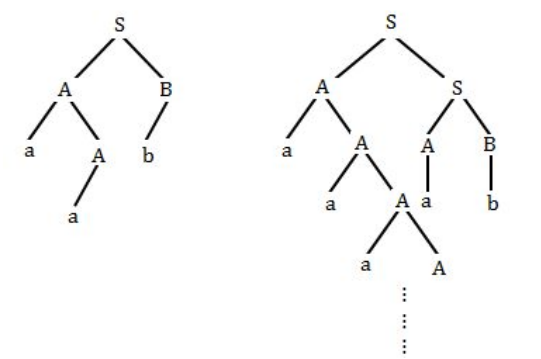
It is clearly representing
aa*b
Question 2 |
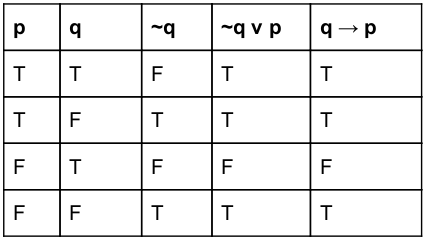
The proposition ~q ∨ p is equivalent to :
Not given any option | |
Not given any option | |
Not given any option | |
Not given any option | |
~q ∨ p ≣ q → p |
Question 2 Explanation:
Options are not given. Excluded for evaluation.
~q ∨ p ≣ q → p

~q ∨ p ≣ q → p
Question 3 |
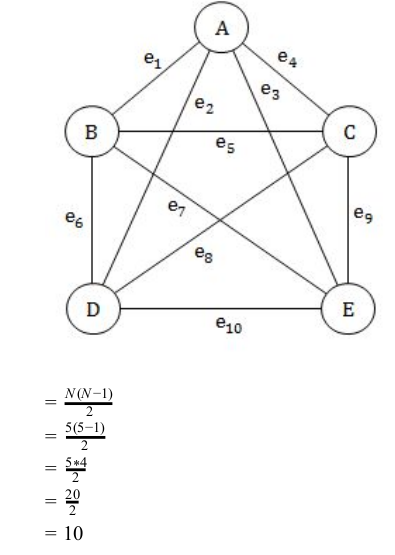
The number of edges in a complete graph with N vertices is equal to :
N (N−1) | |
2N−1 | |
N−1 | |
N(N−1)/2 |
Question 3 Explanation:
N =5

Question 4 |
Which of the following is not true ?
Not given any option | |
A – B = A ∩~B | |
Not given any option | |
Not given any option |
Question 4 Explanation:
A−B= A−(A∩B)
= A-(A∩B)
= A∩(A∩B)’
= A∩(A’ ∩ B’)
= (A∩A’)U(A∩B’)
= U(A∩B’)
= ∅ U ( A ∩ B’)
= A ∩ B’
= A-(A∩B)
= A∩(A∩B)’
= A∩(A’ ∩ B’)
= (A∩A’)U(A∩B’)
= U(A∩B’)
= ∅ U ( A ∩ B’)
= A ∩ B’
Question 5 |
If (a 2 −b 2 ) is a prime number where a and b ε N, then :
(a 2 −b 2 ) =3 | |
(a 2 −b 2 ) =a−b | |
(a 2 −b 2 ) =a+b | |
(a 2 −b 2 ) =5 |
Question 5 Explanation:
→ For any given numbers a and b which belongs to natural numbers , the options (A) and (D) are false
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, ...}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value.
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, ...}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value.
Question 6 |
The hexadecimal equivalent of (10111) 2 ×(1110) 2 is :
150 | |
241 | |
142 | |
101011110 |
Question 6 Explanation:
Step-1: First convert binary number into decimal number
(10111) 2 = (23) 10
(1110) 2 = (14) 10
Step-2: Perform multiplication 23*14=(322) 10
Step-3: Convert (322) 10 into hexadecimal number (322) 10 = (142) 16
(10111) 2 = (23) 10
(1110) 2 = (14) 10
Step-2: Perform multiplication 23*14=(322) 10
Step-3: Convert (322) 10 into hexadecimal number (322) 10 = (142) 16
Question 7 |
An example of a self complementing code is :
8421 code | |
Gray code | |
Excess-3 code | |
7421 code |
Question 7 Explanation:
→ Excess-3 code is also called Self-Complementing Code. Because 1’s complement of excess-3 number is equivalent to 9’s complement of corresponding decimal digit.
→ In excess-3 code, each of the 4-bit number represents decimal digit which is 3 less than actual decimal digit. So the bits have no fixed weight.
→ Excess-3 code is neither CRC nor Algebraic Code which are used for error detection and/or correction.
→ In excess-3 code, each of the 4-bit number represents decimal digit which is 3 less than actual decimal digit. So the bits have no fixed weight.
→ Excess-3 code is neither CRC nor Algebraic Code which are used for error detection and/or correction.
Question 8 |
A sum of products expression can be implemented with __________ logic gates.
AND − OR | |
NAND − OR | |
AND − NOT | |
OR − AND |
Question 8 Explanation:
A sum of products expression can be implemented with AND-OR logic gates.
Ex: (AB)+(BC)+(CD)
Ex: (AB)+(BC)+(CD)
Question 9 |
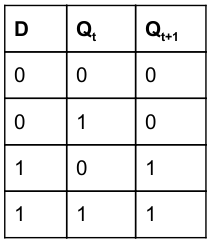
The characteristic equation of the D flip-flop is :
Not option given | |
Q=D | |
Q=1 | |
Q=0 | |
Q t+1 =D |
Question 9 Explanation:
D flip flop characteristic equation truth table:

Q t+1 = DQ' + DQ
Q t+1 =D
Q t+1 = DQ' + DQ
Q t+1 =D
Question 10 |
Which of the following logic is the fastest ?
RTL | |
ECL | |
HTL | |
HCL |
Question 10 Explanation:
Emitter Coupled Logic (ECL)
The storage time is eliminated as the transistors are used in difference amplifier mode and are never driven into saturation.
1. Fastest among all logic families
2. Lowest propagation delay.
Resistor Transistor Logic (RTL)
Sometimes also transistor–resistor logic (TRL) is a class of digital circuits built using resistors as the input network and bipolar junction transistors (BJTs) as switching devices. RTL is the earliest class of transistorized digital logic circuit used; other classes include diode–transistor logic (DTL) and transistor–transistor logic (TTL).
The storage time is eliminated as the transistors are used in difference amplifier mode and are never driven into saturation.
1. Fastest among all logic families
2. Lowest propagation delay.
Resistor Transistor Logic (RTL)
Sometimes also transistor–resistor logic (TRL) is a class of digital circuits built using resistors as the input network and bipolar junction transistors (BJTs) as switching devices. RTL is the earliest class of transistorized digital logic circuit used; other classes include diode–transistor logic (DTL) and transistor–transistor logic (TTL).
Question 11 |
When a function is recursively called, all automatic variables :
are initialized during each execution of the function | |
are retained from the last execution | |
are maintained in a stack | |
are ignored |
Question 11 Explanation:
→ When a function is recursively called, all automatic variables are initialized during each execution of the function.
→ Automatic local variables primarily applies to recursive lexically-scoped languages. An automatic variable is a local variable which is allocated and deallocated automatically when program flow enters and leaves the variable's scope. The scope is the lexical context, particularly the function or block in which a variable is defined.
Question 12 |
Enumeration variables can be used in :
search statement like an integer variable | |
break statement | |
preprocessor commands | |
function statement |
Question 12 Explanation:
→ Enumeration variables can be used in search statement like an integer variable.
→ The enumerator names are usually identifiers that behave as constants in the language. An enumerated type can be seen as a degenerate tagged union of unit type. A variable that has been declared as having an enumerated type can be assigned any of the enumerators as a value.
→ In ‘C’ language exposes the integer representation of enumeration values directly to the programmer. Integers and enum values can be mixed freely, and all arithmetic operations on enum values are permitted. It is even possible for an enum variable to hold an integer that does not represent any of the enumeration values.
→ The enumerator names are usually identifiers that behave as constants in the language. An enumerated type can be seen as a degenerate tagged union of unit type. A variable that has been declared as having an enumerated type can be assigned any of the enumerators as a value.
→ In ‘C’ language exposes the integer representation of enumeration values directly to the programmer. Integers and enum values can be mixed freely, and all arithmetic operations on enum values are permitted. It is even possible for an enum variable to hold an integer that does not represent any of the enumeration values.
There are 12 questions to complete.
