GATE 2003
Question 1 |
Consider the following C function.
float f(float x, int y)
{
float p, s; int i;
for (s=1, p=1, i=1; i < y; i ++)
{
p*= x/i;
s+=p;
}
return s;
}
For large values of y, the return value of the function f best approximates
Xy | |
ex | |
ln(1+x) | |
Xx |
S = S+P
Iteration 1:
P=1; i=1; S=1
P=x
S = 1+x
Iteration 2:
P=x; S = 1+x; i=2
P = x * x/2 = x2/2
Iteration 3:
P = x2/2; S = 1+x+x2/2; i=3
P = (x2/2)(x/3) = x3/6
S = 1 + x + x2/2 + x3/6
Continue upto n
Then f( ) returns:
S = 1 + x/1 + x2/2⋅1 + x3/3⋅2 + ...
= 1 + x/1! + x2/2! + x3/3! + ... + xn/n!
= ex
Question 2 |
Assume the following C variable declaration
int *A [10], B[10][10];
Of the following expressions
I. A[2] II. A[2][3] III. B[1] IV. B[2][3]
which will not give compile-time errors if used as left hand sides of assignment statements in a C program?
I, II, and IV only | |
II, III, and IV only | |
II and IV only | |
IV only |
ii) A[2][3] This results an integer, no error will come.
iii) B[1] is a base address of an array. This will not be changed it will result a compile time error.
iv) B[2][3] This also results an integer. No error will come.
Question 3 |
Let P(E) denote the probability of the event E. Given P(A) = 1, P(B) = 1/2, the values of P(A|B) and P(B|A) respectively are
1/4, 1/2 | |
1/2, 1/4 | |
1/2, 1 | |
1, 1/2 |
P(A/B) = P(A∩B)/P(B)
= P(A)⋅P(B)/P(B) (consider P(A), P(B) are two independent events)
= 1
P(B/A) = P(B∩A)/P(A)
= P(B)⋅P(A)/P(A)
= 1/2
Question 4 |
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that (i) each is sorted in ascending order, (ii) B has 5 and C has 3 elements, and (iii) the result of merging B and C gives A?
2 | |
30 | |
56 | |
256 |
→ If we are pick 3 elements from 8 sequence integers then remaining 5 elements are already in ascending order. After merging these elements then it gives A.
→ No. of possibilities of choosing 8 elements from total of 8 = 8C3
= 8!/3!5!
= 8 * 7
= 56
Question 5 |
n couples are invited to a party with the condition that every husband should be accompanied by his wife. However, a wife need not be accompanied by her husband. The number of different gatherings possible at the party is
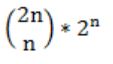 | |
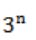 | |
 | |
 |
i) Both husband and wife comes
ii) Only wife comes
iii) Both are not come
The no. of different gatherings possible at party is
= 3 * 3 * 3 * 3 * ... n times
= 3n
Question 6 |
Let T(n) be the number of different binary search trees on n distinct elements. Then ![]() , where x is
, where x is
n – k + 1 | |
n – k | |
n – k – 1 | |
n – k – 2 |

Question 7 |
Consider the set ∑* of all strings over the alphabet ∑ = {0, 1}. ∑* with the concatenation operator for strings
does not form a group | |
forms a non-commutative group | |
does not have a right identity element | |
forms a group if the empty string is removed from Σ*
|
→ To perform concatenation with the given set can result a Monoid and it follows the property of closure, associativity and consists of identity element.
Question 8 |
Let G be an arbitrary graph with n nodes and k components. If a vertex is removed from G, the number of components in the resultant graph must necessarily lie between
k and n | |
k – 1 and k + 1 | |
k – 1 and n – 1 | |
k + 1 and n – k |
If a vertex is removed then it results that all the components are also be disconnected. So removal can create (n-1) components.
Question 9 |
Assuming all numbers are in 2's complement representation, which of the following numbers is divisible by 11111011?
11100111 | |
11100100 | |
11010111 | |
11011011 |
MSB bit is '1' then all numbers are negative
1's complement = 00000100
2's complement = 00000100 + 00000001 = 00000101 = -5
(A) 11100111 - (-25)10
(B) 11100100 - (-28)10
(C) 11010111 - (-41)10
(D) 11011011 - (-37)10
Answer: Option A (-25 is divisible by -5)
Question 10 |
For a pipelined CPU with a single ALU, consider the following situations
I. The j + 1-st instruction uses the result of the j-th instruction as an operand II. The execution of a conditional jump instruction III. The j-th and j + 1-st instructions require the ALU at the same time
Which of the above can cause a hazard?
I and II only | |
II and III only | |
III only | |
All the three |
II is belongs to the Control hazard.
III is belongs to the Structural hazard.
→ Hazards are the problems with the instruction pipeline in CPU micro architectures.
Question 11 |
Consider an array multiplier for multiplying two n bit numbers. If each gate in the circuit has a unit delay, the total delay of the multiplier is
Θ (1) | |
Θ (log n) | |
Θ (n) | |
Θ (n2) |
The total time is n+kn-k = Θ(n)
Question 12 |
Ram and Shyam have been asked to show that a certain problem Π is NP-complete. Ram shows a polynomial time reduction from the 3-SAT problem to Π, and Shyam shows a polynomial time reduction from Π to 3-SAT. Which of the following can be inferred from these reductions?
Π is NP-hard but not NP-complete
| |
Π is in NP, but is not NP-complete
| |
Π is NP-complete | |
Π is neither NP-hard, nor in NP
|
Question 13 |
Nobody knows yet if P = NP. Consider the language L defined as follows:
Which of the following statements is true?
L is recursive | |
L is recursively enumerable but not recursive | |
L is not recursively enumerable | |
Whether L is recursive or not will be known after we find out if P = NP |
P = NP (or) P != NP
→ If P=NP then L=(0+1)* which is regular, then it is recursive.
→ If P!=NP then L becomes ɸ which is also regular, then it is recursive.
So, finally L is recursive.
Question 14 |
The regular expression 0*(10*)* denotes the same set as
(1*0)*1* | |
0+(0+10)* | |
(0+1)*10(0+1)* | |
None of the above |
Option (B) and (C) doesn't generate 11.
Question 15 |
If the strings of a language L can be effectively enumerated in lexicographic (i.e., alphabetic) order, which of the following statements is true?
L is necessarily finite
| |
L is regular but not necessarily finite | |
L is context free but not necessarily regular | |
L is recursive but not necessarily context free |
The give 'L' is recursive but not necessarily context free.
Question 16 |
Which of the following suffices to convert an arbitrary CFG to an LL(1) grammar?
Removing left recursion alone | |
Factoring the grammar alone | |
Removing left recursion and factoring the grammar | |
None of the above |
To convert an arbitrary CFG to an LL(1) grammar we need to remove the left recursion and as well as left factoring without that we cannot convert.
Question 17 |
Assume that the SLR parser for a grammar G has n1 states and the LALR parser for G has n2 states. The relationship between n1 and n2 is:
n1 is necessarily less than n2 | |
n1 is necessarily equal to n2
| |
n1 is necessarily greater than n2
| |
None of the above |
Question 18 |
In a bottom-up evaluation of a syntax directed definition, inherited attributes can
always be evaluated | |
be evaluated only if the definition is L-attributed | |
be evaluated only if the definition has synthesized attributes | |
never be evaluated |
L-Attributed definitions are a class of syntax directed definitions whose attributes can be evaluated by a single traversal of the parse-tree.
Question 19 |
Suppose the numbers 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the usual ordering on natural numbers. What is the in-order traversal sequence of the resultant tree?
7 5 1 0 3 2 4 6 8 9 | |
0 2 4 3 1 6 5 9 8 7 | |
0 1 2 3 4 5 6 7 8 9 | |
9 8 6 4 2 3 0 1 5 7 |

Inorder: 0 1 2 3 4 5 6 7 8 9
Question 20 |
Consider the following three claims
I. (n + k)m = Θ(nm), where k and m are constants II. 2n+1 = O(2n) III. 22n+1 = O(2n)
Which of these claims are correct?
I and II
| |
I and III | |
II and III | |
I, II, and III |
Which is true by considering leading ordered term present in polynomial expression.
II) 2n+1 = Θ(nm) → True
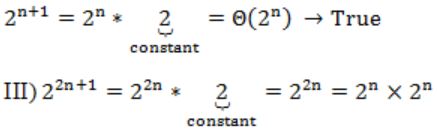
2n×2n can't be written as Θ(2n)
So, this is False.
Question 21 |
Consider the following graph
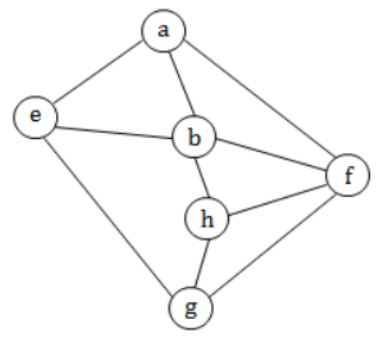
Among the following sequences:
(I) a b e g h f (II) a b f e h g (III) a b f h g e (IV) a f g h b e
Which are depth first traversals of the above graph?
I, II and IV only | |
I and IV only | |
II, III and IV only | |
I, III and IV only |
II) a → b → f → e (✖️)
III) a → b → f → h → g → e (✔️)
IV) a → f → g → h → b → e (✔️)
Question 22 |
The usual Θ(n2) implementation of Insertion Sort to sort an array uses linear search to identify the position where an element is to be inserted into the already sorted part of the array. If, instead, we use binary search to identify the position, the worst case running time will
remain Θ(n2) | |
become Θ(n (log n)2) | |
become Θ(n log n) | |
become Θ(n) |
Instead, linear search use binary search then (log n) will be the worst case time complexity of binary search and performing n swaps to place an element in right position for the corresponding n elements
i.e., n×(logn+n)
Θ((n×logn)+n2)
Θ(n2)
Remains same.
