GATE 2006-IT
Question 1 |
In a certain town, the probability that it will rain in the afternoon is known to be 0.6. Moreover, meteorological data indicates that if the temperature at noon is less than or equal to 25°C, the probability that it will rain in the afternoon is 0.4. The temperature at noon is equally likely to be above 25°C, or at/below 25°C. What is the probability that it will rain in the afternoon on a day when the temperature at noon is above 25°C?
0.4 | |
0.6 | |
0.8 | |
0.9 |
0.6 = (0.5×0.4) + (0.5×P(rain at temp>25)
0.6 = (2) + (0.5×P(rain at temp>25)
P(rain at temp>25) = 0.8
Question 2 |
For the set N of natural numbers and a binary operation f : N x N → N, an element z ∊ N is called an identity for f, if f (a, z) = a = f(z, a), for all a ∊ N. Which of the following binary operations have an identity?
- 1. f(x,y) = x + y - 3
2. f(x,y) = max(x, y)
3. f(x,y) = xy
1 and 2 only | |
2 and 3 only | |
1 and 3 only | |
None of these |
y = 3
Here, identity element is 3.
(2) f(x, y) = max(x, y) = x = max(y, x)
⇒ y = 1
Here, identity element = 1
(3) f(x, y) = xny is not equal to f(y, x) = ynx
So, no identity element.
Question 3 |
In the automaton below, s is the start state and t is the only final state.

Consider the strings u = abbaba, v = bab, and w = aabb. Which of the following statements is true?
The automaton accepts u and v but not w | |
The automaton accepts each of u, v, and w | |
The automaton rejects each of u, v, and w | |
The automaton accepts u but rejects v and w |
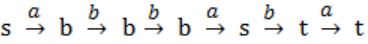
where t is final state
(ii) v = bab
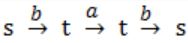
s is not final state
(iii) w = aabb
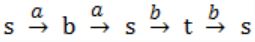
s is not final state
Question 4 |
In the context-free grammar below, S is the start symbol, a and b are terminals, and ϵ denotes the empty string
S → aSa | bSb | a | b | ϵWhich of the following strings is NOT generated by the grammar?
aaaa | |
baba | |
abba | |
babaaabab |
Given string accepts all palindromes.
Option B → baba is not palindrome.
So, this is not accepted by S.
Question 5 |
Which regular expression best describes the language accepted by the non-deterministic automaton below?
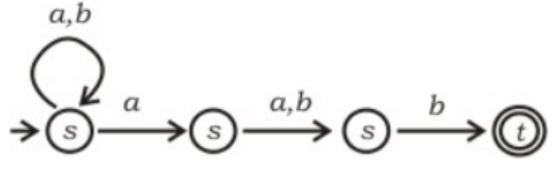
(a + b)* a(a + b)b | |
(abb)* | |
(a + b)* a(a + b)* b(a + b)* | |
(a + b)* |

Question 6 |
Given a Boolean function f (x1, x2, …, xn), which of the following equations is NOT true.
f (x1, x2, …, xn) = x1’f(x1, x2, …, xn) + x1f(x1, x2, …, xn) | |
f (x1, x2, …, xn) = x2f(x1, x2, …, xn) + x2’f(x1, x2, …, xn) | |
f (x1, x2, …, xn) = xn’f(x1, x2, …, 0) + xnf(x1, x2, …,1) | |
f (x1, x2, …, xn) = f(0, x2, …, xn) + f(1, x2, .., xn) |
LHS: f(x1) = 0 where x1 = 0
LHS: f(x1) = 1 when x
RHS: f(0) + f(1) = 0 + 1 = always 1
Question 7 |
The addition of 4-bit, two’s complement, binary numbers 1101 and 0100 results in
0001 and an overflow | |
1001 and no overflow | |
0001 and no overflow | |
1001 and an overflow |
2's complement of 1100 = 1100
Add = 1111
Now convert 1111 to normal form.
⇒ 0000 (1's complement)
⇒ 0001 (2's complement) No carry bit.
Question 8 |
Which of the following DMA transfer modes and interrupt handling mechanisms will enable the highest I/O band-width?
Transparent DMA and Polling interrupts | |
Cycle-stealing and Vectored interrupts | |
Block transfer and Vectored interrupts | |
Block transfer and Polling interrupts |
→ In case of cycle stealing in each cycle time derive send data then wait again few CPU cycle it sends to memory. So, option B is wrong.
→ In case of polling CPU takes the initiative. So I/O bandwidth cannot be high. So, option D is wrong.
→ Consider block transfer in each single block device. Send data so bandwidth must be high. This makes option (C) correct.
Question 9 |
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
10 | |
11 | |
12 | |
15 |
No. of 1 degree nodes = 5
No. of 2 degree nodes = 10
Total no. of edges = (1*5) + (2*10) = 5 + 20 = 25
So, Total no. of edges = 25 + 1 = 26 (No. of nodes in a tree is 1 more than no. of edges)
Total no. of leaf nodes (node with 0 degree) = 26 - 5 - 10 = 11
Question 10 |
A problem in NP is NP-complete if
It can be reduced to the 3-SAT problem in polynomial time | |
The 3-SAT problem can be reduced to it in polynomial time | |
It can be reduced to any other problem in NP in polynomial time | |
Some problem in NP can be reduced to it in polynomial time
|
Question 11 |
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a
Hamiltonian cycle | |
grid | |
hypercube | |
tree |
If all edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is minimum spanning tree.
Question 12 |
In the working-set strategy, which of the following is done by the operating system to prevent thrashing?
1. It initiates another process if there are enough extra frames.
2. It selects a process to suspend if the sum of the sizes of the working-sets exceeds the total number of available frames.
1 only | |
2 only | |
Neither 1 nor 2 | |
Both 1 and 2 |
Question 13 |
The process state transition diagram of an operating system is as given below.
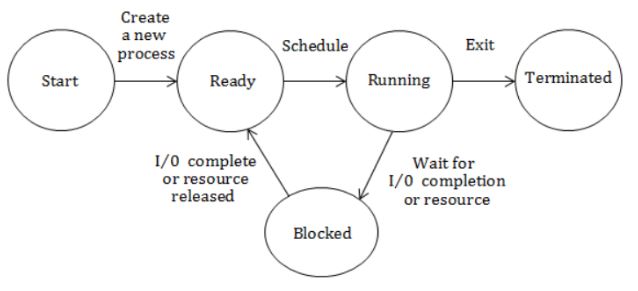
Which of the following must be FALSE about the above operating system?
It is a multiprogrammed operating system | |
It uses preemptive scheduling | |
It uses non-preemptive scheduling | |
It is a multi-user operating system |
Question 14 |
Consider the relations r1(P, Q, R) and r2(R, S, T) with primary keys P and R respectively. The relation r1 contains 2000 tuples and r2 contains 2500 tuples. The maximum size of the join r1⋈ r2 is :
2000 | |
2500 | |
4500 | |
5000 |
Question 15 |
Which of the following relational query languages have the same expressive power?
1. Relational algebra
2. Tuple relational calculus restricted to safe expressions
3. Domain relational calculus restricted to safe expressions
2 and 3 only | |
1 and 2 only | |
1 and 3 only | |
1, 2 and 3 |
Question 16 |
The cyclomatic complexity of the flow graph of a program provides
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at most once | |
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at most once | |
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once | |
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at least once |
Question 17 |
With respect to software testing, consider a flow graph G with one connected component. Let E be the number of edges, N be the number of nodes, and P be the number of predicate nodes of G. Consider the following four expressions:
1. E - N + P
2. E - N + 2
3. P + 2
4. P + 1
The cyclomatic complexity of G is given by
1 or 3 | |
2 or 3 | |
2 or 4 | |
1 or 4 |
Question 18 |
HELO and PORT, respectively, are commands from the protocols
FTP and HTTP | |
TELNET and POP3 | |
HTTP and TELNET | |
SMTP and FTP |
Question 19 |
Which of the following statements is TRUE?
Both Ethernet frame and IP packet include checksum fields | |
Ethernet frame includes a checksum field and IP packet includes a CRC field | |
Ethernet frame includes a CRC field and IP packet includes a checksum field | |
Both Ethernet frame and IP packet include CRC fields |

IP packet:

IP Datagram:

Question 20 |
Which of the following statement(s) is TRUE?
1. A hash function takes a message of arbitrary length and generates a fixed length code.
2. A hash function takes a message of fixed length and generates a code of variable length.
3. A hash function may give the same hash value for distinct messages.
1 only | |
2 and 3 only | |
1 and 3 only | |
2 only |
(2) Statement-2 is wrong, refer statement-1.
(3) Statement-3 is correct, for example hash function N%10, this will generate same values for 1 as well as 2!
Question 21 |
Consider the following first order logic formula in which R is a binary relation symbol.
∀x∀y (R(x, y) => R(y, x))The formula is
satisfiable and valid | |
satisfiable and so is its negation | |
unsatisfiable but its negation is valid | |
satisfiable but its negation is unsatisfiable |
