GATE 2008-IT
Question 1 |
A set of Boolean connectives is functionally complete if all Boolean functions can be synthesized using those. Which of the following sets of connectives is NOT functionally complete?
EX-NOR | |
implication, negation | |
OR, negation | |
NAND |
→ NOR and NAND are the functionally complete logic gates, OR, AND, NOT only logic gate can be implemented by using them.
→ And (Implication, Negation) is also functionally complete.
Question 2 |
A sample space has two events A and B such that probabilities P(A ∩ B) = 1/2, P(A') = 1/3, P(B') = 1/3. What is P(A ∪ B)?
11/12 | |
10/12 | |
9/12 | |
8/12 |
P(A') = 1/3; P(A) = 2/3
P(B') = 1/3; P(B) = 2/3
P(A ∪ B) = P(A) +P(B) - P(A ∩ B)
= 2/3 + 2/3 - 1/2
= 4+4-3/ 6
= 5/6
= 10/12
Question 3 |
What is the chromatic number of the following graph?
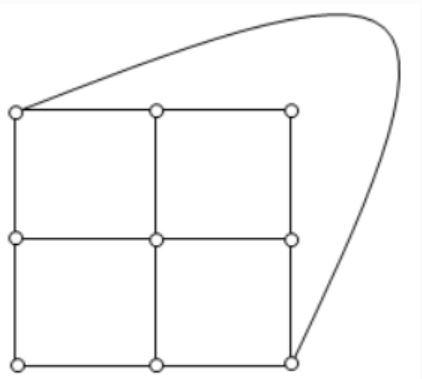
2 | |
3 | |
4 | |
5 |
→ Chromatic number of a graph is the smallest number of colours needed to colour the vertices so that no two adjacent vertices share the same colour.
Question 4 |
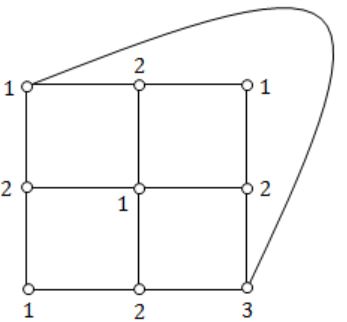
What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?
5 | |
4 | |
3 | |
2 |
(2, 5, 8) is the maximal independent set for a chain of 9 nodes. If we add any start node to the set then it will not be MIS.
Independent set:
A set of vertices is called independent set such that no two vertices in the set are adjacent.
Question 5 |
Which of the following regular expressions describes the language over {0, 1} consisting of strings that contain exactly two 1’s?
(0 + 1) * 11(0 + 1) * | |
0 * 110 * | |
0 * 10 * 10 * | |
(0 + 1) * 1(0 + 1) * 1 (0 + 1) *
|
→ 1110 this consists of 3 ones but accepted by given expression. So this is false.
Option B: 0* 110*
→ 0101 this string consists of two is but not accepted by given expression. This is false.
Option C: 0* 10* 10*
→ This is true.
Option D: (0+1)* 1(0+1)* 1(0+1)*
→ 011010 - This can have three is but accepted by given expression. So this is also false.
Question 6 |
Let N be an NFA with n states and let M be the minimized DFA with m states recognizing the same language. Which of the following in NECESSARILY true?
m ≤ 2n | |
n ≤ m | |
M has one accept state | |
m = 2n |
A state in a DFA is a proper subset of states of NFA of corresponding DFA.
→ No. of subsets with n elements = 2n
→ m ≤ 2n
Question 7 |
The following bit pattern represents a floating point number in IEEE 754 single precision format
110000011101000000000000000000000The value of the number in decimal form is
-10 | |
-13 | |
-26 | |
None of these |
Exponent bits - 10000011
Exponent can be added with 127 bias in IEEE single precision format then outval exponent
= 10000011 - 127
= 131 - 127
= 4
→ In IEEE format, an implied 1 is before mantissa, and hence the outval number is
→ 1.101 × 24 = -(11010)2 = -26
Question 8 |
Consider the following Boolean function of four variables
f(A,B,C,D) = Σ(2, 3, 6, 7, 8, 9, 10, 11, 12, 13)The function is
independent of one variable | |
independent of two variables | |
independent of three variable | |
dependent on all the variables |
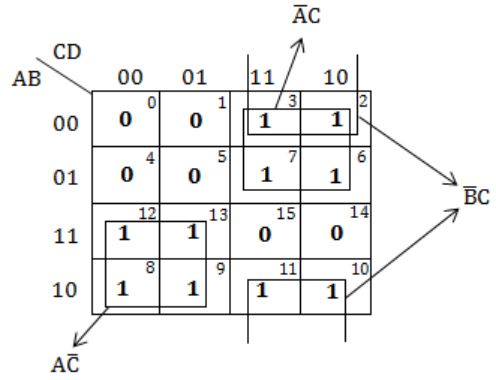
Independent of one variable '0'.
Question 9 |
What Boolean function does the circuit below realize ?

xz+x’z’ | |
xz’+x’z | |
x’y’+yz | |
xy+y’z’ |
= (x’z’ + xz)’
= x’z + xz’
Question 10 |
Arrange the following functions in increasing asymptotic order:
A. n1/3 B. en C. n7/4 D. n log9n E. 1.0000001n
A, D, C, E, B | |
D, A, C, E, B | |
A, C, D, E, B | |
A, C, D, B, E |
n1/3 < n log9 < n7/4 < 1.0000001n < en
Question 11 |
For problems X and Y, Y is NP-complete and X reduces to Y in polynomial time. Which of the following is TRUE?
If X can be solved in polynomial time, then so can Y | |
X is NP-complete | |
X is NP-hard | |
X is in NP, but not necessarily NP-complete |
Question 12 |
Which of the following is TRUE?
The cost of searching an AVL tree is θ (log n) but that of a binary search tree is O(n) | |
The cost of searching an AVL tree is θ (log n) but that of a complete binary tree is θ (n log n) | |
The cost of searching a binary search tree is O (log n) but that of an AVL tree is θ(n) | |
The cost of searching an AVL tree is θ (n log n) but that of a binary search tree is O(n) |
Question 13 |
Match the programming paradigms and languages given in the following table.

I-c, II-d, III-b, IV-a | |
I-a, II-d, III-c, IV-b | |
I-d, II-c, III-b, IV-a | |
I-c, II-d, III-a, IV-b |
Question 14 |
Consider the execution of the following commands in a shell on a linux operating system.
system bash$cat alpha Mathematics bash$in alpha beta bash$ rm alpha bash$cat >> beta << SAME Information Technology SANE bash$ cat betaThe output of the last command will be:
Mathematics Information Technology SAME. | |
Mathematics Information Technology. | |
Information Technology. | |
Information Technology SAME. |
Question 15 |
A processor that has carry, overflow and sign flag bits as part of its program status word (PSW) performs addition of the following two 2's complement numbers 01001101 and 11101001. After the execution of this addition operation, the status of the carry, overflow and sign flags, respectively will be:
1, 1, 0 | |
1, 0, 0 | |
0, 1, 0 | |
1, 0, 1 |

Carry flag = 1
Overflow flag = 0
Sign bit = 0 (MSB bit is 0)
Overflow flag:
In computer processors, the overflow flag is usually a single bit in a system status register used to indicate when an arithmetic overflow has occurred in an operation.
Question 16 |
A paging scheme uses a Translation Look-aside Buffer (TLB). A TLB-access takes 10 ns and a main memory access takes 50 ns. What is the effective access time(in ns) if the TLB hit ratio is 90% and there is no page-fault?
54 | |
60 | |
65 | |
75 |
= 10 + 0.1 × 50 + 50
= 10 + 5 + 50
= 65
Question 17 |
Find if the following statements in the context of software testing are TRUE or FALSE.
(S1) Statement coverage cannot guarantee execution of loops in a program under test.
(S2) Use of independent path testing criterion guarantees execution of each loop in a program under test more than once.
True, True | |
True, False | |
False, True | |
False, False |
Question 18 |
How many bytes of data can be sent in 15 seconds over a serial link with baud rate of 9600 in asynchronous mode with odd parity and two stop bits in the frame?
10,000 bytes | |
12,000 bytes | |
15,000 bytes | |
27,000 bytes |
1 bit for start bit, 8 bits for data, 1 bit for parity, 2 bits for stop bits i.e.,
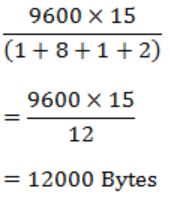
Question 19 |
Which of the following is TRUE only of XML but NOT HTML?
It is derived from SGML | |
It describes content and layout | |
It allows user defined tags | |
It is restricted only to be used with web browsers |
Question 20 |
Provider the best matching between the entries in the two columns given in the table below:

I-a, II-d, III-c, IV-b | |
I-b, II-d, III-c, IV-a | |
I-a, II-c, III-d, IV-b | |
I-b, II-c, III-d, IV-a |
(ii) Kazaa and DC++ are P2P applications.
(iii) P2P slip is a processor of PPP.
(iv) DNS allows caching of entries at local server.
Question 21 |
Which of the following first order formula is logically valid? Here α(x) is a first order formula with x as a free variable, and β is a first order formula with no free variable.
[β→(∃x,α(x))]→[∀x,β→α(x)] | |
[∃x,β→α(x)]→[β→(∀x,α(x))] | |
[(∃x,α(x))→β]→[∀x,α(x)→β] | |
[(∀x,α(x))→β]→[∀x,α(x)→β] |
L.H.S. : If there is an x such that α(x) is true, then β is true.
R.H.S. : For all x, if α(x) true, then β is true.
Here, the given LHS and RHS are to be same as β is a formula which can be independent of x (if β is true for one x, it is true for every x, and vice-versa).
Here, LHS = RHS
So, Option C is valid.
