GATE 2012
Question 1 |
Consider the following logical inferences.
- I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I2: If it rains then the cricket match will not be played.
It did not rain.
Inference: The cricket match was played.
Which of the following is TRUE?
Both I1 and I2 are correct inferences | |
I1 is correct but I2 is not a correct inference | |
I1 is not correct but I2 is a correct inference | |
Both I1 and I2 are not correct inferences |
The cricket match was played.
Let p = it rains
q = playing cricket/ match played
If (it rains) then (the match will not be played)
p ⇒ (∼q)
Inference: There was no rain. (i.e., p = F)
So for any F ⇒ (∼q) is true.
So this inference is valid.
I2: If it rains then the cricket match will not be played.
It did not rain.
p ⇒ (∼q)
Inference: The cricket match was played.
q = T
p ⇒ (∼q)
p ⇒ (∼T)
p ⇒ F
This is false for p = T, so this is not true.
Question 2 |
Which of the following is TRUE?
Every relation in 3NF is also in BCNF | |
A relation R is in 3NF if every non-prime attribute of R is fully functionally dependent on every key of R | |
Every relation in BCNF is also in 3NF | |
No relation can be in both BCNF and 3NF |
Question 3 |
What will be the output of the following C program segment?
char inchar = 'A';
switch (inchar)
{
case 'A' :
printf ("choice A n") ;
case 'B' :
printf ("choice B ") ;
case 'C' :
case 'D' :
case 'E' :
default:
printf ("No Choice") ;
}No Choice | |
Choice A | |
 | |
Program gives no output as it is erroneous |
So,
→ Choice A
→ Choice B. No choice. Is the output.
Question 4 |
Assuming P ≠ NP, which of the following is TRUE?
NP-complete = NP | |
NP-complete ∩ P = ∅ | |
NP-hard = NP | |
P = NP-complete |
The definition of NP-complete is,
A decision problem p is NP-complete if:
1. p is in NP, and
2. Every problem in NP is reducible to p in polynomial time.
It is given that assume P ≠ NP , hence NP-complete ∩ P = ∅ .
This is due to the fact that, if NP-complete ∩ P ≠ ∅ i.e. there are some problem (lets say problem P1) which is in P and in NP-complete also, then it means that P1 (NP-complete problem) can be solved in polynomial time also (as it is also in P class) and this implies that every NP problem can be solve in polynomial time, as we can convert every NP problem into NP-complete problem in polynomial time.
Which means that we can convert every NP problem to P1 and solve in polynomial time and hence P = NP, which is contradiction to the given assumption that P ≠ NP.
Question 5 |
The worst case running time to search for an element in a balanced binary search tree with n2n elements is
Θ (n log n) | |
Θ (n2n) | |
Θ (n) | |
Θ (log n) |
→ No of elements = n.2n then search time = (log n.2n)
= (log n + log 2n)
= (log n + n log 2)
= O(n)
Question 6 |
The truth table
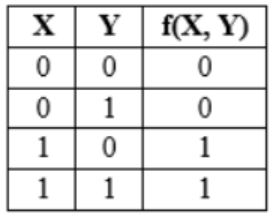
represents the Boolean function
X | |
X + Y | |
X ⊕ Y | |
Y |
Question 7 |
The decimal value 0.5 in IEEE single precision floating point representation has
fraction bits of 000…000 and exponent value of 0 | |
fraction bits of 000…000 and exponent value of −1 | |
fraction bits of 100…000 and exponent value of 0 | |
no exact representation |
So, value of the exponent = -1
and
fraction is 000…000 (Implicit representation)
Question 8 |
A process executes the code
fork(); fork(); fork();
The total number of child processes created is
3 | |
4 | |
7 | |
8 |
7 are child processes.
Question 9 |
Consider the function f(x) = sin(x) in the interval x ∈ [π/4, 7π/4]. The number and location(s) of the local minima of this function are
One, at π/2 | |
One, at 3π/2 | |
Two, at π/2 and 3π/2 | |
Two, at π/4 and 3π/2 |
f’(x) = cos x
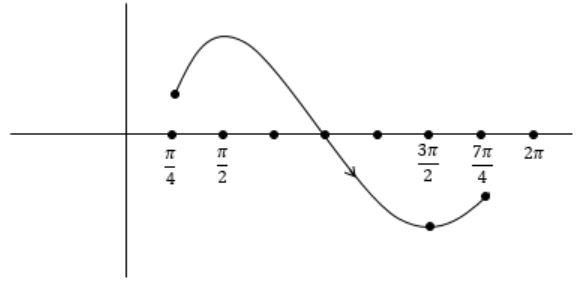
[just consider the given interval (π/4, 7π/4)]
f'(x) = 0 at π/2, 3π/2
To get local minima f ’’(x) > 0, f ’’(x) = - sin x
f ’’(x) at π/2, 3π/2
f ’’(x) = -1< 0 local maxima
f ’’ (3π/2) = 1 > 0 this is local minima
In the interval [π/4, π/2] the f(x) is increasing, so f(x) at π/4 is also a local minima.
So there are two local minima for f(x) at π/4, 3π/2.
Question 10 |
The protocol data unit (PDU) for the application layer in the Internet stack is
Segment | |
Datagram | |
Message | |
Frame |
Question 11 |
Let A be the 2×2 matrix with elements a11 = a12 = a21 = +1 and a22 = -1. Then the eigenvalues of the matrix A19 are
1024 and -1024 | |
1024√2 and -1024√2 | |
4√2 and -4√2 | |
512√2 and -512√2 |
The 2×2 matrix =
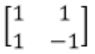
Cayley Hamilton theorem:
If matrix A has ‘λ’ as eigen value, An has eigen value as λn.
Eigen value of

|A-λI| = 0

-(1-λ)(1+λ)-1 = 0
-(1-λ2 )-1 = 0
-1 = 1-λ2
λ2 = 2
λ = ±√2
A19 has (√2)19 = 29×√2 (or) (-√2)19 = -512√2
= 512√2
Question 12 |
What is the complement of the language accepted by the NFA shown below?
Assume Σ={a} and ε is the empty string.
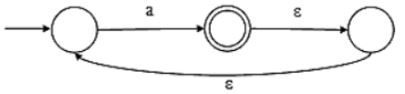
∅ | |
{ε} | |
a* | |
{a ,ε} |
Hence the complement of language is: {a* − a+} = {ϵ}
Question 13 |
What is the correct translation of the following statement into mathematical logic?
“Some real numbers are rational”
∃x (real(x) ∨ rational(x)) | |
∀x (real(x) → rational(x)) | |
∃x (real(x) ∧ rational(x)) | |
∃x (rational(x) → real(x)) |

∃x (real(x) ∧ rational(x))
(A) ∃x(real(x) ∨ rational(x))
means There exists some number, which are either real or rational.
(B) ∀x (real(x)→rational(x))
If a number is real then it is rational.
(D) ∃x (rational(x)→real(x))
There exists a number such that if it is rational then it is real.
Question 14 |
Given the basic ER and relational models, which of the following is INCORRECT?
An attribute of an entity can have more than one value | |
An attribute of an entity can be composite | |
In a row of a relational table, an attribute can have more than one value | |
In a row of a relational table, an attribute can have exactly one value or a NULL value |
Option (B): In ER model, the attribute which can be further broken down into some other attributes is called composite attribute.
Option (C): In Relational model, the intersection of one row and column should contain only one value. So, option (C) is INCORRECT.
Option (D): In Relational model, the intersection of one row and column should contain either exactly one value or NULL.
Question 15 |
Which of the following statements are TRUE about an SQL query?
-
P:An SQL query can contain a HAVING clause even if it does not have a GROUP BY clause.
Q:An SQL query can contain a HAVING clause even if it has a GROUP BY clause.
R: All attributes used in the GROUP BY clause must appear in the SELECT clause.
S: Not all attributes used in the GROUP BY clause need to appear in the SELECT clause
P and R | |
P and S | |
Q and R | |
Q and S |
The HAVING Clause enables you to specify conditions that filter which group results appear in the results. The WHERE clause places conditions on the selected columns, whereas the HAVING clause places conditions on groups created by the GROUP BY clause. So, we cannot use HAVING clause without GROUP BY clause.
Question 16 |
The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem with n discs is
T(n) = 2T(n - 2) + 2 | |
T(n) = 2T(n - 1) + n | |
T(n) = 2T(n/2) + 1 | |
T(n) = 2T(n - 1) + 1 |
T(n) = 2T(n – 1) + 1
= 2 [2T(n – 2) + 1] + 1
= 22 T(n – 2) + 3
⋮
= 2k T( n – k) + (2k – 1)
n – k = 1
= 2n-1 T(1) + (2n-1 – 1)
= 2n-1 + 2n-1 – 1
= 2n – 1
≌ O(2n)
