HCU PHD CS MAY 2014
Question 1 |
One way of showing that one string is equal to another string is to compare and match them character by character. What happens if we allow both the strings to be of infinite length?
The method fails because we can only show that the two strings are not equal.
| |
The method fails because we can only show that the two strings are equal. | |
The method works correctly and tells if the strings are equal or not. | |
The method works only if the strings are numeric. |
Question 2 |
In the C Programming Language, arrays can be defined in two ways. The first is static: int a[4000] [3000];
the second is dynamic: declare as int **a;
and then allocate memory using malloc() . Which of the following is TRUE?
In the first case, memory is contiguous while in the second case, memory is not contiguous.
| |
In the first case, elements may be accessed as a[i] [j], while in the second, they cannot be accessed so. | |
In the first case, the array elements are stored in row-major order, while in the second they are stored in column-major order. | |
None of the above. |
Question 2 Explanation:
In the first case the array is contiguoaus while in the second case array is not contiguos because in the second case the declaration is array of ponters to pointers.
Question 3 |
If flexibility is defined as having maximum choice in cache placement, which of the following is correctly ordered in ascending order of flexibility?
Direct Mapping, Set-Associative Mapping, Associative Mapping | |
Set-Associative Mapping, Direct Mapping, Associative Mapping | |
Associative Mapping, Set-Associative Mapping, Direct Mapping
| |
None of the above. |
Question 3 Explanation:
In direct mapping only choice is there.
In set associative mapping of set size k,there are k choices.
While in associative mapping the choice is any block of cache.
Hence ascending order of flexibility is ,
Direct mapping , Set associative Mapping, Associative mapping.
In set associative mapping of set size k,there are k choices.
While in associative mapping the choice is any block of cache.
Hence ascending order of flexibility is ,
Direct mapping , Set associative Mapping, Associative mapping.
Question 4 |
Heap sort may be considered as
Insertion sort done on a heap data structure instead of a list. | |
Selection sort done on a heap data structure instead of a list. | |
Bubble sort done on a heap data structure instead of a list. | |
None of the above. |
Question 4 Explanation:
When we do min or max heapify in heap sort, we get the min or max element in the root then we exchange it with the last element. And we repeat the procedure for the remaining element .
We do similar type in selection sort,we find min or max element and then we exchange that element with first element and we repeat the element with the remaining procedure .
We do similar type in selection sort,we find min or max element and then we exchange that element with first element and we repeat the element with the remaining procedure .
Question 5 |
Which of the following is NOT a feature of the Von Neumann architecture?
Storage space for programs. | |
Storage space for data | |
Unique next instruction for execution. | |
Separating instructions from data. |
Question 6 |
The correct result of Lexicographically sorting
109, 20, 119, 2,207, 27, 19
in ascending order is:
19, 109, 119, 2, 20, 27, 207 | |
109, 119, 19, 2,20,27,207 | |
109, 119, 19, 2,20,207,27 | |
2, 19, 20, 27, 109, 119 , 207 |
Question 6 Explanation:
Lexicographical sorting of numbers is similar to the Lexicographical sorting of words in a dictionary.
So the correct answer is,
109,119,19,2,20,207,27
So the correct answer is,
109,119,19,2,20,207,27
Question 7 |
All IP addresses in the range 186.220.64.0 to 186.220.71.254 are kept in a VLAN.
The correct netmask so that messages are broadcast only within this VLAN is
186.220.255.255 | |
186.220.248.0 | |
186.220.248.0 | |
186.220.8.0 |
Question 7 Explanation:
We have to select such subnet mask by which ANDing the both IP address we get the same network ID.
And option D gives same network ID after ANDing .The network ID we get is 186.220.0.0
Question 8 |
Which sentence can be generated by: S → aS | bA, A → d | ccA
aadb | |
bccddd | |
aabccd | |
None of the above |
Question 8 Explanation:
S ⟶ aS
⟶ aaS (∵ S ⟶ aS)
⟶ aabA (∵ S ⟶ bA)
⟶ aabccA (∵ A ⟶ ccA)
⟶ aabccd (∵ A ⟶ d)
⟶ aaS (∵ S ⟶ aS)
⟶ aabA (∵ S ⟶ bA)
⟶ aabccA (∵ A ⟶ ccA)
⟶ aabccd (∵ A ⟶ d)
Question 9 |
Which sort uses features of the key to operate in Linear time relative to the number
of elements in the array?
Quick Sort | |
Merge Sort | |
Radix Sort | |
Bubble Sort |
Question 9 Explanation:
Examples of sorting algorithms that run in linear time are counting sort, radix sort and bucket sort. Counting sort and radix sort assume that the input consists of integers in a small range.
Question 10 |
Convert FAFAFA in hexadecimal into octal.
76767676 | |
76737672 | |
76727672 | |
76575372 |
Question 10 Explanation:
Hexadecimal number consists of 4 bit binary no. An octal number is comprising of 3 bit binary no.
So first we will convert the Hexadecimal number into binary no. and then by taking each 3 bit from right side we will convert it into octal no.
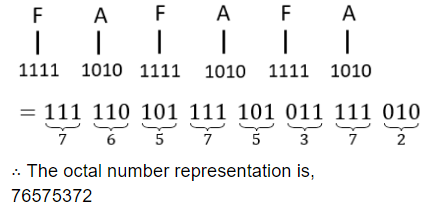
So first we will convert the Hexadecimal number into binary no. and then by taking each 3 bit from right side we will convert it into octal no.

Question 11 |
Which of the following decision procedures does NOT have exponential time complexity?
Graph-colouring Problem | |
Travelling Salesperson Problem | |
Hamiltonian Circuit Problem | |
Linear Programming Problem |
Question 12 |
Simplify the following boolean expression: 2xyz' + xy'z' + x'yz'?
xy + y'z' + x'y | |
xy + xz' + x'z' | |
(y + z')x | |
(x + y)z' |
Question 12 Explanation:
2xyz’ + xy’z’ + x’yz’
= xyz’ + xyz’ + xy’z’ + x’yz’
= xyz’ + x’yz’ + xyz’ + xy’z’
= yz’ (x + x’) + xz’ (y + y’)
= yz’ + xz’
= z’(y + x)
= xyz’ + xyz’ + xy’z’ + x’yz’
= xyz’ + x’yz’ + xyz’ + xy’z’
= yz’ (x + x’) + xz’ (y + y’)
= yz’ + xz’
= z’(y + x)
Question 13 |
Which of the following problems is solvable?
Determining if a universal Turing machine and some input will halt | |
Writing a universal Turing machine | |
Determining if a universal Turing machine can be written in fewer than k instructions for some k | |
Determining if an arbitrary Turing machine is a universal Turing machine |
Question 13 Explanation:
Universal Turing Machine is a machine which can simulate the work of other turing machine.Also universal TM can accept any other machine's input other than itself.
Now lets check option wise,
A) It is the halting problem of turing machine which is undecidable.
B) Universal turing machine cannot recognize its own action,so undecidable.
C) By rice’s theorem it is undecidable.
D) If a TM can simulate the work of any other TM, then it will be UTM. Here definite "yes" and "no" ans possible. So, will be decidable
Now lets check option wise,
A) It is the halting problem of turing machine which is undecidable.
B) Universal turing machine cannot recognize its own action,so undecidable.
C) By rice’s theorem it is undecidable.
D) If a TM can simulate the work of any other TM, then it will be UTM. Here definite "yes" and "no" ans possible. So, will be decidable
Question 14 |
How many possible bytes have exactly three bits on (i.e., bit=true)?
8*7 | |
8*7*6 | |
8*3
| |
None of the above |
Question 15 |
What is the value of F(4) using the following procedure?
function F(k: integer) : integer;
begin
if (k<3) then F:=k
else F := F(k-1)*f(k-2)+F(k-3);
end;
5 | |
6 | |
7 | |
8 |
Question 15 Explanation:
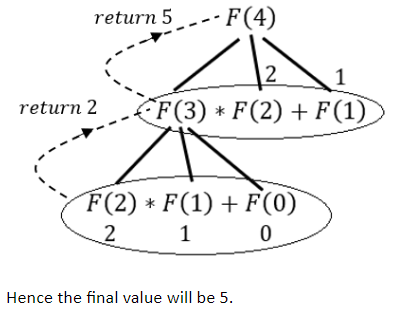
Question 16 |
Queues serve a major role in:
simulation of recursion | |
simulation of arbitrary linked lists | |
expression evaluation | |
simulation of limited resource allocation |
Question 16 Explanation:
Queues serve a major role in simulation of limited resource allocation .
Stack serves major role in simulation of recursion and expression evaluation.
Stack serves major role in simulation of recursion and expression evaluation.
Question 17 |
What is True for a complete bipartite graph K(3,3)?
it is a planar graph | |
it requires three colours to be minimally coloured | |
it is non-planar | |
it is isomorphic to K(2,4) |
Question 17 Explanation:
The graph K(5) and K(3,3) are two of the most important graphs within the subject of planarity in graph theory.Kuratowski’s theorem tells us that if we can find the subgraph in any graph that is homeomorphic to K(5) or K(3,3) then the graph is not planar,meaning its not possible for the edges to be redrawn such that they are none overlapping. Of course this theorem relies on the fact that K(5) and K(3,3) are themselves are not planar.
Question 18 |
A complete binary tree of level 5 has how many nodes?
15 | |
63 | |
25 | |
71 | |
None of the above |
Question 18 Explanation:
Tree with 5 levels of nodes has height 4. So the no. of nodes in a complete binary tree is of height 4 is
2^(4+1) - 1 = 2^5 - 1 = 31
2^(4+1) - 1 = 2^5 - 1 = 31
There are 18 questions to complete.
