ISRO-2017 December
Question 1 |
Suppose A is a finite set with n elements. The number of elements and the rank of the largest equivalence relation on A is
{n,1} | |
{n, n} | |
{n2, 1} | |
{1, n2} |
Question 1 Explanation:
Let us assume a set with 4 elements
S={1,2,3,4}
→ If a set is said to be equivalence, then the set must be
i) Reflexive
ii) Symmetric
iii) Transitive
i) Reflexive Relation: A relation ‘R’ on a set ‘A’ is said to be reflexive if (xRx)∀x∈A.
A = {1,2,3}

R = {(1,1), (2,2), (3,3)}
R = {(1,1), (2,2)} It is false.
R = {(1,1), (2,2), (3,3), (1,2)}
ii) Symmetric Relation: A relation on a set A is said to be symmetric if (xRy). Then (yRx)∀x,y∈A i.e., if ordered pair (x,y)∈R. Then (y,x)∈R ∀x,y∈A.
A={1,2,3}
R1={(1,2), (2,1)}
R2={(1,1), (2,2), (3,3), (1,2), (2,1), (2,3), (3,2)}
Transitive Relation:
A relation ‘R’ on a set ‘A’ is said to be transitive if (xRy) and (yRz), then (xRz)∀(x,y,z∈A).
A={1,2,3}
R1={ }
R2={(1,1)}
R3={(1,2), (3,1)}
R4={(1,2), (2,1), (1,1)}
⇾ A={1,2,3,4}
Largest ordered set is
S×S={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}
⇒ Total = 16 = 42 = n2
Smallest ordered set = {(1,1),(2,2),(3,3),(4,4)}
⇒ Total=4=n
Note: In question, they are clearly mentioned that Rank of an Equivalence relation is equal to the number of induced Equivalence classes. Since we have maximum number of ordered pairs(which are reflexive, symmetric and transitive ) in largest Equivalence relation, its rank is always 1.
S={1,2,3,4}
→ If a set is said to be equivalence, then the set must be
i) Reflexive
ii) Symmetric
iii) Transitive
i) Reflexive Relation: A relation ‘R’ on a set ‘A’ is said to be reflexive if (xRx)∀x∈A.
A = {1,2,3}

R = {(1,1), (2,2), (3,3)}
R = {(1,1), (2,2)} It is false.
R = {(1,1), (2,2), (3,3), (1,2)}
ii) Symmetric Relation: A relation on a set A is said to be symmetric if (xRy). Then (yRx)∀x,y∈A i.e., if ordered pair (x,y)∈R. Then (y,x)∈R ∀x,y∈A.
A={1,2,3}
R1={(1,2), (2,1)}
R2={(1,1), (2,2), (3,3), (1,2), (2,1), (2,3), (3,2)}
Transitive Relation:
A relation ‘R’ on a set ‘A’ is said to be transitive if (xRy) and (yRz), then (xRz)∀(x,y,z∈A).
A={1,2,3}
R1={ }
R2={(1,1)}
R3={(1,2), (3,1)}
R4={(1,2), (2,1), (1,1)}
⇾ A={1,2,3,4}
Largest ordered set is
S×S={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}
⇒ Total = 16 = 42 = n2
Smallest ordered set = {(1,1),(2,2),(3,3),(4,4)}
⇒ Total=4=n
Note: In question, they are clearly mentioned that Rank of an Equivalence relation is equal to the number of induced Equivalence classes. Since we have maximum number of ordered pairs(which are reflexive, symmetric and transitive ) in largest Equivalence relation, its rank is always 1.
Question 2 |
Consider the set of integers I. Let D denote “divides with an integer quotient” (e.g. 4D8 but 4D7). Then D is
Reflexive, not symmetric, transitive | |
Not reflexive, not antisymmetric, transitive | |
Reflexive, antisymmetric, transitive | |
Not reflexive, not antisymmetric, not transitive |
Question 2 Explanation:
Reflexive Relation:
A relation ‘R’ on a set ‘A’ is said to be reflexive if (xRx)∀x∈A.
Example: 4 D 8, 4 D 12, 4 D16, 4 D20…….(Here, D means divide)
8 D 16, 8 D 24……….
In this example, we didn’t get 4D4. So, it is not reflexive.
AntiSymmetric Relation:
For all x ∈ I, R(x,y) and R(y,x) then x=y is antisymmetric. We can easily make a violation as R(-2,2) and R(2,-2) are not antisymmetric.
It is violating. So, not antisymmetric relation.
Transitive relation:
A relation ‘R’ on a set ‘A’ is said to be transitive if (xRy) and (yRz), then (xRz)∀(x,y,z∈A).
Example: 4D8, 4D12, 4D16, 4D20…….(Here, D means divide)
8D16, 8D24……….
{ 4D8, 8D16, 1D16}. So, it is satisfied.
A relation ‘R’ on a set ‘A’ is said to be reflexive if (xRx)∀x∈A.
Example: 4 D 8, 4 D 12, 4 D16, 4 D20…….(Here, D means divide)
8 D 16, 8 D 24……….
In this example, we didn’t get 4D4. So, it is not reflexive.
AntiSymmetric Relation:
For all x ∈ I, R(x,y) and R(y,x) then x=y is antisymmetric. We can easily make a violation as R(-2,2) and R(2,-2) are not antisymmetric.
It is violating. So, not antisymmetric relation.
Transitive relation:
A relation ‘R’ on a set ‘A’ is said to be transitive if (xRy) and (yRz), then (xRz)∀(x,y,z∈A).
Example: 4D8, 4D12, 4D16, 4D20…….(Here, D means divide)
8D16, 8D24……….
{ 4D8, 8D16, 1D16}. So, it is satisfied.
Question 3 |
A bag contains 19 red balls and 19 black balls. Two balls are removed at a time repeatedly and discarded if they are of the same colour, but if they are different, black ball is discarded and red ball is returned to the bag. The probability that this process will terminate with one red ball is
1 | |
1/21 | |
0 | |
0.5 |
Question 3 Explanation:
Given data,
Step-1: Bag contains 19 Red(R) and 19 Blue(B) balls.
BB (or) RR happen we are discarded.
If we get BR (or) RB then B is discarded and R is returned.
Step-2: There are some conditions that,
→ If black balls will either come with black then both black balls are discarder.
→ If it will come with red then only black balls will be discarded.
→ Suppose 2 red balls will come together means we are discarding both red balls.
Step-3: As per the above constraints, total 19 Red balls it means odd number.
→ Among 19 only 18 will be discarded.
Step-3: Final content of bag at second last trail will be either R,B (or) R,R,R and finally in last
trail bag will left with one red ball in both the cases.
Step-1: Bag contains 19 Red(R) and 19 Blue(B) balls.
BB (or) RR happen we are discarded.
If we get BR (or) RB then B is discarded and R is returned.
Step-2: There are some conditions that,
→ If black balls will either come with black then both black balls are discarder.
→ If it will come with red then only black balls will be discarded.
→ Suppose 2 red balls will come together means we are discarding both red balls.
Step-3: As per the above constraints, total 19 Red balls it means odd number.
→ Among 19 only 18 will be discarded.
Step-3: Final content of bag at second last trail will be either R,B (or) R,R,R and finally in last
trail bag will left with one red ball in both the cases.
Question 4 |
If x = -1 and x = 2 are extreme points of f(x) = α log |x| + βx2 + x then
α = -6, β = -1/2 | |
α = 2, β = -1/2 | |
α = 2, β = 1/2 | |
α = -6, β =1/2 |
Question 4 Explanation:
Given data,
Step-1: x= -1 and x=2
f(x) = α log |x| + β x2 + x
f'(x)= α/x + 2βx + 1 = 0
Step-2: for extreme points f'(x)=0
α/x + 2βx + 1=0
Step-3: For x= -1 then we will get α+2β= 1 → (i)
For x= 2: then we will get α+8β= 2 → (ii)
from (i) and (ii) we can get the value of α=2 and β= -1/2
Step-1: x= -1 and x=2
f(x) = α log |x| + β x2 + x
f'(x)= α/x + 2βx + 1 = 0
Step-2: for extreme points f'(x)=0
α/x + 2βx + 1=0
Step-3: For x= -1 then we will get α+2β= 1 → (i)
For x= 2: then we will get α+8β= 2 → (ii)
from (i) and (ii) we can get the value of α=2 and β= -1/2
Question 5 |
Let f(x) = log|x| and g(x) = sin x . If A is the range of f(g(x)) and B is the range of g(f(x)) then A ∩ B is
[-1, 0] | |
[-1, 0) | |
[-∞, 0] | |
[-∞,1] |
Question 5 Explanation:
Given data,
Step-1: f(x) = log|x| and given range is [-∞ to +∞]
g(x) = sin(x) and given range is [-1,1]
Step-2: Given 2 variables are A and B
A= f(g(x))
= log|g(x)|
= log|sin(x)|
So, we will get A range is [-∞ ,0]
Step-3: B= g(f(x))
= sin(f(x))
= sin(log|x|)
So, we will get B range is [-1, 1]
Step-4: Common in both A and B is A∩B
A∩B = [-1, 0]
Key point: Ranges [ -1 ≤ sin(x) ≤ 1 and -∞ ≤ log|x| ≤ ∞ ]
Step-1: f(x) = log|x| and given range is [-∞ to +∞]
g(x) = sin(x) and given range is [-1,1]
Step-2: Given 2 variables are A and B
A= f(g(x))
= log|g(x)|
= log|sin(x)|
So, we will get A range is [-∞ ,0]
Step-3: B= g(f(x))
= sin(f(x))
= sin(log|x|)
So, we will get B range is [-1, 1]
Step-4: Common in both A and B is A∩B
A∩B = [-1, 0]
Key point: Ranges [ -1 ≤ sin(x) ≤ 1 and -∞ ≤ log|x| ≤ ∞ ]
There are 5 questions to complete.
ISRO DEC 2017 22- Soon
Question 1 |
Which of the following are context free?
A = {anbnambm | m, n>=0}
B = {anbnambn | m, n>=0}
C = {ambn | m≠2n,m, n>=0}
A = {anbnambm | m, n>=0}
B = {anbnambn | m, n>=0}
C = {ambn | m≠2n,m, n>=0}
A and B only | |
A and C only | |
B and C only | |
C only |
Question 1 Explanation:
Statement-A: When 'a' will comes as input. We will push it on the top of stack and when 'b' will comes as input after 'a' we will pop one 'a' for each 'b'.
This way language 'A' can be accepted by the push down automat. Hence A is CFL.
Statement-B: When last 'b' i.e., bn after am comes as input then top of the stack will contain am
So we can't compare an with anbn. Hence it is not CFL
Statement-C: It is a CFL
This way language 'A' can be accepted by the push down automat. Hence A is CFL.
Statement-B: When last 'b' i.e., bn after am comes as input then top of the stack will contain am
So we can't compare an with anbn. Hence it is not CFL
Statement-C: It is a CFL
Question 2 |
Let S be an NP-complete problem. Q and R are other two problems not known to be NP. Q is polynomial time reducible to S and S is polynomial time reducible to R. Which of the following statements is true?
R is NP-complete | |
R is NP-hard | |
Q is NP-complete | |
Q is NP-hard |
Question 2 Explanation:
NP-Hard- if it can be solved in polynomial time then all NP-Complete can be solved in polynomial time. If NP Hard problem is reducible to another problem in Polynomial Time, then that problem is also NP Hard which means every NP problem can be reduced to this problem in Polynomial Time.
Question 3 |
The number of structurally different possible binary trees with 4 nodes is
14 | |
12 | |
336 | |
168 |
Question 3 Explanation:
Finding number of binary tree, we are using catalan numbers formula
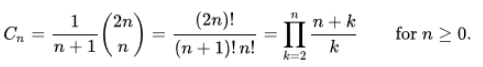
Here, n=4.
Total number of binary trees are 14.
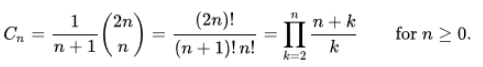
Here, n=4.
Total number of binary trees are 14.
Question 4 |
Using public key cryptography, X adds a digital signature σ to a message M, encrypts (M,σ) and sends it to Y, where it is decrypted. Which one of the following sequence of keys is used for operations?
Encryption : X’s private key followed by Y’s private key. Decryption : X’s public key followed by Y’s public key. | |
Encryption : X’s private key followed by Y’s public key; Decryption : X’s public key followed by Y’s private key | |
Encryption : X’s private key followed by Y’s public key; Decryption : Y’s private key followed by X’s public key. | |
Encryption : X’s public key followed by Y’s private key; Decryption : Y’s public key followed by X’s private key. |
Question 4 Explanation:

Encryption: Source has to encrypt with its private key for forming Digital signature for Authentication. Source has to encrypt the (M, σ) with Y’s public key to send it confidentially. Decryption: Destination Y has to decrypt first with its private key, then decrypt using source public key.
Question 5 |
Which of the following are used to generate a message digest by the network security protocols?
(P) SHA-256
(Q) AES
(R) DES
(S) MD5
(P) SHA-256
(Q) AES
(R) DES
(S) MD5
P and S only | |
P and Q only | |
R and S only | |
P and R only |
Question 5 Explanation:
To generate a message digest by the network security protocols we need SHA and MD5.
→ SHA-256 and SHA-512 are novel hash functions computed with 32-bit and 64-bit words, respectively. They use different shift amounts and additive constants, but their structures are otherwise virtually identical, differing only in the number of rounds.
→ The MD5 message-digest algorithm is a widely used hash function producing a 128-bit hash value. Although MD5 was initially designed to be used as a cryptographic hash function, it has been found to suffer from extensive vulnerabilities. It can still be used as a checksum to verify data integrity, but only against unintentional corruption. It remains suitable for other non-cryptographic purposes, for example for determining the partition for a particular key in a partitioned database.
→ SHA-256 and SHA-512 are novel hash functions computed with 32-bit and 64-bit words, respectively. They use different shift amounts and additive constants, but their structures are otherwise virtually identical, differing only in the number of rounds.
→ The MD5 message-digest algorithm is a widely used hash function producing a 128-bit hash value. Although MD5 was initially designed to be used as a cryptographic hash function, it has been found to suffer from extensive vulnerabilities. It can still be used as a checksum to verify data integrity, but only against unintentional corruption. It remains suitable for other non-cryptographic purposes, for example for determining the partition for a particular key in a partitioned database.
Question 6 |
In the IPv4 addressing format, the number of networks allowed under Class C addresses is
220 | |
224 | |
214 | |
221 |
Question 6 Explanation:
→ IP address belonging to class C are assigned to small-sized networks.
The network ID is 24 bits long.
The host ID is 8 bits long.
→ The higher order bits of the first octet of IP addresses of class C are always set to 110. The remaining 21 bits are used to determine network ID.
→ The 8 bits of host ID is used to determine the host in any network. The default subnet mask for class C is 255.255.255.x. Class C has a total of:
221 = 2097152 network address
28 – 2 = 254 host address
IP addresses belonging to class C ranges from 192.0.0.x – 223.255.255.x.
The network ID is 24 bits long.
The host ID is 8 bits long.
→ The higher order bits of the first octet of IP addresses of class C are always set to 110. The remaining 21 bits are used to determine network ID.
→ The 8 bits of host ID is used to determine the host in any network. The default subnet mask for class C is 255.255.255.x. Class C has a total of:
221 = 2097152 network address
28 – 2 = 254 host address
IP addresses belonging to class C ranges from 192.0.0.x – 223.255.255.x.
Question 7 |
An Internet Service Provider (ISP) has the following chunk of CIDR-based IP addresses available with it: 245.248.128.0/20. The ISP wants to give half of this chunk of addresses to Organization A, and a quarter to Organization B, while retaining the remaining with itself. Which of the following is a valid allocation of addresses to A and B?
245.248.136.0/21 and 245.248.128.0/22 | |
245.248.128.0/21 and 245.248.128.0/22 | |
245.248.132.0/22 and 245.248.132.0/21 | |
245.248.136.0/24 and 245.248.132.0/21 |
Question 7 Explanation:
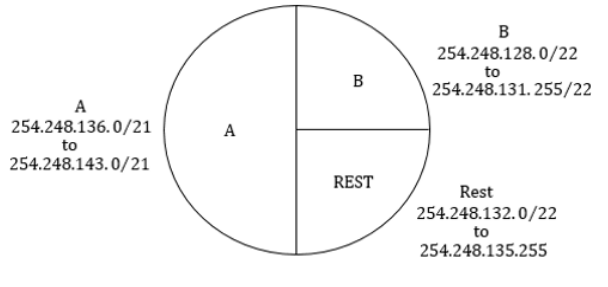
Question 8 |
Assume that Source S and Destination D are connected through an intermediate router R. How many times a packet has to visit the network layer and data link layer during a transmission from S to D?
Network layer – 4 times, Data link layer – 4 times | |
Network layer – 4 times, Data link layer – 6 times | |
Network layer – 2 times, Data link layer – 4 times | |
Network layer – 3 times, Data link layer – 4 times |
Question 8 Explanation:
Source and destination are hosts. The hosts have all layers but routers have only 3 layers
i.e physical,data link and network layer. The purpose of routers is to just pass on the packet between hosts or networks.
Therefore ,

Therefore ,

Question 9 |
Generally TCP is reliable and UDP is not reliable. DNS which has to be reliable uses UDP because
UDP is slower | |
DNS servers has to keep connections | |
DNS requests are generally very small and fit well within UDP segments | |
None of these |
Question 9 Explanation:
→ UDP is cheap.
→ UDP itself is not reliable, but higher level protocols - as DNS - may maintain reliability, e.g. by repeating the UDP datagram in the case of no response.
→ But the last is not the case for DNS. DNS itself uses sometimes besides UDP (as its primary protocol) the reliable Transmission Control Protocol (TCP).
→ The last is used when the response data size exceeds 512 bytes, and for tasks which require the reliable delivery (e.g. zone transfers).
→ UDP is much faster. TCP is slow as it requires 3 way handshake. The load on DNS servers is also an important factor. DNS servers (since they use UDP) don’t have keep connections.
→ DNS requests are generally very small and fit well within UDP segments.
→ UDP is not reliable, but reliability can added on application layer. An application can use UDP and can be reliable by using timeout and resend at application layer.
→ UDP itself is not reliable, but higher level protocols - as DNS - may maintain reliability, e.g. by repeating the UDP datagram in the case of no response.
→ But the last is not the case for DNS. DNS itself uses sometimes besides UDP (as its primary protocol) the reliable Transmission Control Protocol (TCP).
→ The last is used when the response data size exceeds 512 bytes, and for tasks which require the reliable delivery (e.g. zone transfers).
→ UDP is much faster. TCP is slow as it requires 3 way handshake. The load on DNS servers is also an important factor. DNS servers (since they use UDP) don’t have keep connections.
→ DNS requests are generally very small and fit well within UDP segments.
→ UDP is not reliable, but reliability can added on application layer. An application can use UDP and can be reliable by using timeout and resend at application layer.
Question 10 |
Consider the set of activities related to e-mail
A : Send an e-mail from a mail client to mail server
B : Download e-mail headers from mail box and retrieve mails from server to a cache
C : Checking e-mail through a web browser
The application level protocol used for each activity in the same sequence is
A : Send an e-mail from a mail client to mail server
B : Download e-mail headers from mail box and retrieve mails from server to a cache
C : Checking e-mail through a web browser
The application level protocol used for each activity in the same sequence is
SMTP, HTTPS, IMAP | |
SMTP, POP, IMAP | |
SMTP, IMAP, HTTPS | |
SMTP, IMAP, POP | |
None of the above |
Question 10 Explanation:
→ SMTP is used for connecting to outbound servers to send email while POP3 and IMAP are used to connect to incoming servers to retrieve messages.
→ POP download email headers from mailbox and retrieve mails from servers to a cache.
→ HTTPS checking email through a web browser.
→ POP download email headers from mailbox and retrieve mails from servers to a cache.
→ HTTPS checking email through a web browser.
Question 11 |
Station A uses 32 byte packets to transmit messages to Station B using a sliding window protocol. The round trip time delay between A and B is 40 ms and the bottleneck bandwidth on the path A and B is 64 kbps. What is the optimal window size that A should use?
5 | |
10 | |
40 | |
80 |
Question 11 Explanation:
Given data,
-- Round trip delay between A and B = 40ms
-- Station A using frame size = 32 bytes. 32 bytes=32*8 bits
-- Bottleneck bandwidth on the path A and B = 64kbps
-- Window size=?
Step-1: First we have to find transmission time
Transmission time= Frame size/bandwidth
= 32*8/(64) ms
= 4 ms
Step-2: We have to find window size.
Standard Utilization formula is = n/(1+2a)
where ‘a’ is Propagation time / transmission time
= n/(1+2a)
= n/(1+40/4)
= n/11
Maximum utilization is ‘n’ = 11
-- Round trip delay between A and B = 40ms
-- Station A using frame size = 32 bytes. 32 bytes=32*8 bits
-- Bottleneck bandwidth on the path A and B = 64kbps
-- Window size=?
Step-1: First we have to find transmission time
Transmission time= Frame size/bandwidth
= 32*8/(64) ms
= 4 ms
Step-2: We have to find window size.
Standard Utilization formula is = n/(1+2a)
where ‘a’ is Propagation time / transmission time
= n/(1+2a)
= n/(1+40/4)
= n/11
Maximum utilization is ‘n’ = 11
Question 12 |
A two way set associative cache memory unit with a capacity of 16 KB is built using a block size of 8 words. The word length is 32 bits. The physical address space is 4 GB. The number of bits in the TAG, SET fields are
20, 7 | |
19, 8 | |
20, 8 | |
21, 9 |
Question 12 Explanation:
2-way set associative it means 2 cache lines in one set
Physical Address =4GB
Cache Size =16KB
Block Size = 8 words = 8* 32 bits = 256 bits = 32 Bytes -------- because 1 word =32 bits
No.of cache lines /blocks = 16KB/ 32 B = 2^14/ 2^5= 2^9 i.e 512 lines
No of sets = No of cache lines / 2 ---------- because it is 2-way set-associative cache
= 2^9 /2 = 2^8 sets => 8 set bits
Now, because it is set-associative cache memory physical address generated by CPU is divided into 3 parts - first part indicate number of tag bits.
Second part indicates -no of bits required to address each set.
Third part indicates - no. of bits for block offset.
Let suppose tag bits = X
Therefore , we get
X+8+5 = 32 => X= 19 are the tag bits
Physical Address =4GB
Cache Size =16KB
Block Size = 8 words = 8* 32 bits = 256 bits = 32 Bytes -------- because 1 word =32 bits
No.of cache lines /blocks = 16KB/ 32 B = 2^14/ 2^5= 2^9 i.e 512 lines
No of sets = No of cache lines / 2 ---------- because it is 2-way set-associative cache
= 2^9 /2 = 2^8 sets => 8 set bits
Now, because it is set-associative cache memory physical address generated by CPU is divided into 3 parts - first part indicate number of tag bits.
Second part indicates -no of bits required to address each set.
Third part indicates - no. of bits for block offset.
Let suppose tag bits = X
Therefore , we get
X+8+5 = 32 => X= 19 are the tag bits
Question 13 |
A CPU has a 32 KB direct mapped cache with 128 byte block size. Suppose A is a 2 dimensional array of size 512×512 with elements that occupy 8 bytes each. Consider the code segment
for (i =0; i < 512; i++)
{
for (j =0; j < 512; j++)
{
x += A[i][j];
}
}
Assuming that array is stored in order A[0][0], A[0][1], A[0][2]……, the number of cache misses is
for (i =0; i < 512; i++)
{
for (j =0; j < 512; j++)
{
x += A[i][j];
}
}
Assuming that array is stored in order A[0][0], A[0][1], A[0][2]……, the number of cache misses is
16384 | |
512 | |
2048 | |
1024 |
Question 13 Explanation:
→ Access A in row major order.
→ No. of cache blocks=Cache size/Block size = 32KB / 128B = 32×210B / 128B = 215 / 27 = 256
→ No. of array elements in each block = Block size / Element size = 128B / 8B =16
→ Total misses for (P1)=Array size * No. of array elements / No. of cache blocks = (512×512) * 16 / 256=16384
→ No. of cache blocks=Cache size/Block size = 32KB / 128B = 32×210B / 128B = 215 / 27 = 256
→ No. of array elements in each block = Block size / Element size = 128B / 8B =16
→ Total misses for (P1)=Array size * No. of array elements / No. of cache blocks = (512×512) * 16 / 256=16384
Question 14 |
A computer with 32 bit word size uses 2s complement to represent numbers. The range of integers that can be represented by this computer is
–232 to 232 | |
–231 to 232-1 | |
–231 to 231-1 | |
–231-1 to 232-1 |
Question 14 Explanation:
Range of ‘n’ bit 2’s complement binary number is always –2(n-1) to 2(n-1)-1.
There are 14 questions to complete.
