ISRO CS 2015
Question 1 |
Which of the given number has its IEEE-754 32 bit floating point representation as

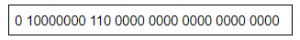
2.5 | |
3.0 | |
3.5 | |
4.5 |
Question 1 Explanation:
→ Sign bit S = 0 (It means positive number)
→ E=1000 0000B = 128D (in normalized form)
→ Fraction is 1.11B (with an implicit leading 1) = 1 + 1×2-1 + 1×2-2
= 1.75D
→ The number is +1.75 × 2(128-127)
= +3.5D
→ E=1000 0000B = 128D (in normalized form)
→ Fraction is 1.11B (with an implicit leading 1) = 1 + 1×2-1 + 1×2-2
= 1.75D
→ The number is +1.75 × 2(128-127)
= +3.5D
Question 2 |
The range of integers that can be represented by an n bit 2’s complement number system is:
– 2n – 1 to 2n – 1 – 1 | |
– (2n – 1 – 1) to (2n – 1 – 1) | |
– 2n – 1 to 2n – 1 | |
– (2n – 1 + 1) to (2n – 1 – 1) |
Question 2 Explanation:
In 2’s complement numbers, the range of integers are from -2n-1 to 2n-1 – 1
Question 3 |
How many 32K X 1 RAM chips are needed to provide a memory capacity of 256K-bytes?
8 | |
32 | |
64 | |
128 |
Question 3 Explanation:
Number of RAM chips required = Memory capacity / RAM chip capacity.
=(256K * 8) / (32K x 1)
=(256*1024*8) / (32*1024*1)
=64
=(256K * 8) / (32K x 1)
=(256*1024*8) / (32*1024*1)
=64
Question 4 |
A modulus -12 ring counter requires a minimum of
10 flip-flops | |
12 flip-flops | |
8 flip-flops | |
6 flip-flops |
Question 4 Explanation:
A ring counter is a type of counter composed of flip-flops connected into a shift register, with the output of the last flip-flop fed to the input of the first, making a "circular" or "ring" structure.
The “MODULO” or “MODULUS” of a counter is the number of states the counter counts or sequences through before repeating itself and a ring counter can be made to output any modulo number. A “mod-n” ring counter will require “n” number of flip-flops connected together to circulate a single data bit providing “n” different output states
So, modulus-12 requires , 12 flip-flops.
The “MODULO” or “MODULUS” of a counter is the number of states the counter counts or sequences through before repeating itself and a ring counter can be made to output any modulo number. A “mod-n” ring counter will require “n” number of flip-flops connected together to circulate a single data bit providing “n” different output states
So, modulus-12 requires , 12 flip-flops.
Question 5 |
The complement of the Boolean expression AB ( B’C + AC ) is
( A’ + B’ ) + ( B + C’ )( A’ + C’ ) | |
( A’ + B’ ) + ( BC’ + A’C’ ) | |
( A’ + B’ )( B + C’) + ( A + C’ ) | |
( A + B )( B’ + C )( A + C ) |
Question 5 Explanation:
→ Finding complement boolean expression, we require Demorgan’s law.
→ DeMorgan’s law and after complementing:
⇒ ( AB ( B’C + AC ))’
⇒ (A + B)’ + (B’C + AC)’
⇒ (A’ + B’) + ( B’C)’ (AC)’
⇒ (A’ + B’) + ( B + C’)(A’ + C’)
→ DeMorgan’s law and after complementing:
⇒ ( AB ( B’C + AC ))’
⇒ (A + B)’ + (B’C + AC)’
⇒ (A’ + B’) + ( B’C)’ (AC)’
⇒ (A’ + B’) + ( B + C’)(A’ + C’)
Question 6 |
The code which uses 7 bits to represent a character is
ASCII | |
BCD | |
EBCDIC | |
Gray |
Question 6 Explanation:
→ ISO/IEC 646, like ASCII, is a 7-bit character set. It does not make any additional codes available, so the same code points encoded different characters in different countries. Escape codes were defined to indicate which national variant applied to a piece of text, but they were rarely used, so it was often impossible to know what variant to work with and, therefore, which character a code represented, and in general, text-processing systems could cope with only one variant anyway.
→ Extended Binary Coded Decimal Interchange Code (EBCDIC) is an 8-bit binary code for numeric and alphanumeric characters.
→ BCD encoding uses 4 bits to represent each digit from the range 0 to 9 in its binary form.
→ In case of Gray codes, any number of bits can be used to represent a character, according to the requirement.
→ Extended Binary Coded Decimal Interchange Code (EBCDIC) is an 8-bit binary code for numeric and alphanumeric characters.
→ BCD encoding uses 4 bits to represent each digit from the range 0 to 9 in its binary form.
→ In case of Gray codes, any number of bits can be used to represent a character, according to the requirement.
Question 7 |
If half adders and full adders are implemented using gates, then for the addition of two 17 bit numbers (using minimum gates) the number of half adders and full adders required will be
0, 17 | |
16, 1 | |
1, 16 | |
8, 8 |
Question 7 Explanation:
1. An adder is a digital circuit that performs addition of numbers. The half adder adds two binary digits called as augend and addend and produces two outputs as sum and carry; XOR is applied to both inputs to produce sum and AND gate is applied to both inputs to produce carry.
2. The full adder adds 3 one bit numbers, where two can be referred to as operands and one can be referred to as bit carried in. And produces 2-bit output, and these can be referred to as output carry and sum.
Half adder is used to add two numbers of the least significant bits, so one half adder is required. In order to add remaining 16 bits of two numbers , we require 16 full adders
2. The full adder adds 3 one bit numbers, where two can be referred to as operands and one can be referred to as bit carried in. And produces 2-bit output, and these can be referred to as output carry and sum.
Half adder is used to add two numbers of the least significant bits, so one half adder is required. In order to add remaining 16 bits of two numbers , we require 16 full adders
Question 8 |
Minimum number of 2x1 multiplexers required to realize the following function,
f = A’B’C + A’B’C’
Assume that inputs are available only in true form and Boolean constant 1 and 0 are available.
f = A’B’C + A’B’C’
Assume that inputs are available only in true form and Boolean constant 1 and 0 are available.
1 | |
2 | |
3 | |
7 |
Question 8 Explanation:
Given function f = A’B’C + A’B’C’
=A’B’(C+C’) (C+C’=1)
=A’B’
=(A+B)’
So we can implement with minimum Two number of 2x1 multiplexers
=A’B’(C+C’) (C+C’=1)
=A’B’
=(A+B)’
So we can implement with minimum Two number of 2x1 multiplexers
Question 9 |
The number of 1’s in the binary representation of (3*4096 + 15*256 + 5*16 + 3) are:
8 | |
9 | |
10 | |
12 |
Question 9 Explanation:
Binary expression of (3*4096 + 15*256 + 5*16 + 3)
=(12,288+3840+80+3)
=(16211)10
=(0011111101010011)2
Total number of 1’s in binary representation is 10.
=(12,288+3840+80+3)
=(16211)10
=(0011111101010011)2
Total number of 1’s in binary representation is 10.
Question 10 |
The boolean expression AB + AB’+ A’C + AC is independent of the boolean variable
A | |
B | |
C | |
None of these |
Question 10 Explanation:
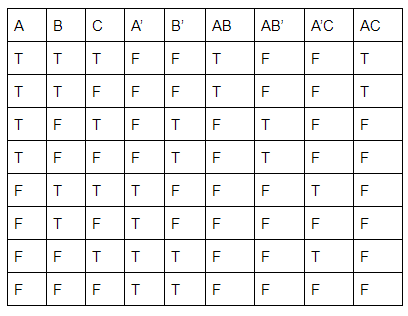
→ AB + AB' + A'C + AC
= A(B + B') + C(A + A')
= A+C
As the expression is independent of 'B'
Question 11 |
If the sequence of operations – push (1), push (2), pop, push (1), push (2), pop, pop, pop, push (2), pop are performed on a stack, the sequence of popped out values
2,2,1,1,2 | |
2,2,1,2,2 | |
2,1,2,2,1 | |
2,1,2,2,2
|
Question 11 Explanation:

Final Pop sequence: 22112
Question 12 |
A machine needs a minimum of 100 sec to sort 1000 names by quick sort. The minimum time needed to sort 100 names will be approximately
50.2 sec | |
6.7 sec | |
72.7 sec | |
11.2 sec |
Question 12 Explanation:
We need to find the minimum time to sort the names by using quick sort.
The Worst case time complexity is O(n2)
Average and best case time complexity is O(n logn)
Step-1: Time taken to sort 1000 names by quicksort
100= c*nlogn
= c*1000log1000
= 100
c=1/10log1000
Now, time taken to sort 100 names by quicksort,
=c*nlogn
= (1/10log1000)*100*log100
= 6.7
The Worst case time complexity is O(n2)
Average and best case time complexity is O(n logn)
Step-1: Time taken to sort 1000 names by quicksort
100= c*nlogn
= c*1000log1000
= 100
c=1/10log1000
Now, time taken to sort 100 names by quicksort,
=c*nlogn
= (1/10log1000)*100*log100
= 6.7
Question 13 |
Six files F1, F2, F3, F4, F5 and F6 have 100, 200, 50, 80, 120, 150 records respectively. In what order should they be stored so as to optimize act. Assume each file is accessed with the same frequency
F3, F4, F1, F5, F6, F2 | |
F2, F6, F5, F1, F4, F3 | |
F1, F2, F3, F4, F5, F6 | |
Ordering is immaterial as all files are accessed with the same frequency. |
Question 13 Explanation:
Optimal merge pattern will give the optimal result after performing sorted order. Every time it will take least frequency elements and performing merging.
→ Final order is F3, F4, F1, F5, F6, F2
→ Final order is F3, F4, F1, F5, F6, F2
Question 14 |
A hash table with ten buckets with one slot per bucket is shown in the following figure. The symbols S1 to S7 initially entered using a hashing function with linear probing. The maximum number of comparisons needed in searching an item that is not present is

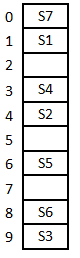
4 | |
5 | |
6 | |
3 |
Question 14 Explanation:
In this, maximum size of cluster = 4 (S6, S3, S7, S1)
→ Worst case of finding a number is equal to maximum size of cluster + 1(after searching all the cluster it enters into empty cluster)
→ Maximum no. of comparisons = 4+1
= 5
→ Worst case of finding a number is equal to maximum size of cluster + 1(after searching all the cluster it enters into empty cluster)
→ Maximum no. of comparisons = 4+1
= 5
Question 15 |
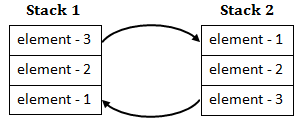
The queue data structure is to be realized by using stack. The number of stacks needed would be
It cannot be implemented | |
2 stacks | |
4 stacks | |
1 stack |
Question 15 Explanation:
Step-1: Pop elements from Stack-1 and push into Stack-2.
For this,
int x=element=stack-1,pop();
stack-2.push(element);

Step-2: Once the complete stack-1 gets copied to Stack-2, then we can simply call pop() on s2, it will remove the element-1.
So, A queue can be implemented using 2 stacks.
For this,
int x=element=stack-1,pop();
stack-2.push(element);
Step-2: Once the complete stack-1 gets copied to Stack-2, then we can simply call pop() on s2, it will remove the element-1.
So, A queue can be implemented using 2 stacks.
Question 16 |
Consider the following Relationship Entity Diagram(ERD)
 Which of the following possible relations will not hold if the above ERD is mapped into a relation model?
Which of the following possible relations will not hold if the above ERD is mapped into a relation model?
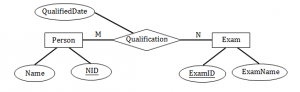 Which of the following possible relations will not hold if the above ERD is mapped into a relation model?
Which of the following possible relations will not hold if the above ERD is mapped into a relation model?Person (NID, Name) | |
Qualification (NID, ExamID, QualifiedDate) | |
Exam (ExamID, NID, ExamName) | |
Exam (ExamID, ExamName) |
Question 16 Explanation:
Given diagram is ER diagram , So any object, for example, entities, attributes of an entity, relationship sets, and attributes of relationship sets, can be represented with the help of an ER diagram.
We need to convert ER diagram to relational model.
There are two entities in the ER diagram named Person and Exam with attributes which are represented in ellipse.
Table name: Person

Now Create table for a relationship
Add the primary keys of all participating Entities as fields of table with their respective data types.
If relationship has any attribute, add each attribute as field of table.
Declare a primary key composing all the primary keys of participating entities.
Declare all foreign key constraints.
Table for “Qualification” relationship

We need to convert ER diagram to relational model.
There are two entities in the ER diagram named Person and Exam with attributes which are represented in ellipse.
Table name: Person

Now Create table for a relationship
Add the primary keys of all participating Entities as fields of table with their respective data types.
If relationship has any attribute, add each attribute as field of table.
Declare a primary key composing all the primary keys of participating entities.
Declare all foreign key constraints.
Table for “Qualification” relationship

Question 17 |
Consider the following log sequence of two transactions on a bank account, with initial balance 12000, that transfer 2000 to a mortgage payment and then apply a 5% interest.
- T1 start
- T1 B old=1200 new=10000
- T1 M old=0 new=2000
- T1 commit
- T2 start
- T2 B old=10000 new=10500
- T2 commit
We must redo log record 6 to set B to 10500 | |
We must undo log record 6 to set B to 10000 and then redo log records 2 and 3 | |
We need not redo log records 2 and 3 because transaction T1 has committed | |
We can apply redo and undo operations in arbitrary order because they are idempotent. |
Question 17 Explanation:
→ When the database system crashes after the transactions have committed then we need to redo the log records.
→ And if the database system crashes before the transactions have committed then we need to undo the log records.
So from above theory we can say that option (B) is the correct Solution.
→ And if the database system crashes before the transactions have committed then we need to undo the log records.
So from above theory we can say that option (B) is the correct Solution.
Question 18 |
Given a block can hold either 3 records or 10 key pointers. A database contains n records, then how many blocks do we need to hold the data file and the dense index
13n/30 | |
n/3 | |
n/10 | |
n/30 |
Question 18 Explanation:
Total number of records in the data base=n
Given block will hold either 3 records or 10 key pointers.
Number of blocks to store “n” records = n/3
Number of blocks to store dense file index = n/10
Total blocks to hold data file and dense index = n/3 + n/10 = 13n/30 blocks.
Given block will hold either 3 records or 10 key pointers.
Number of blocks to store “n” records = n/3
Number of blocks to store dense file index = n/10
Total blocks to hold data file and dense index = n/3 + n/10 = 13n/30 blocks.
Question 19 |
The correct syntax to write “Hi there” in Javascript is
jscript.write (“Hi There”); | |
document.write (“Hi There”); | |
print (“Hi There”); | |
print.jscript (“Hi There”); |
Question 19 Explanation:
JavaScript can "display" data in different ways:
Writing into an HTML element, using innerHTML.
Writing into the HTML output using document.write().
Writing into an alert box, using window.alert().
Writing into the browser console, using console.log().
Writing into an HTML element, using innerHTML.
Writing into the HTML output using document.write().
Writing into an alert box, using window.alert().
Writing into the browser console, using console.log().
Question 20 |
Let R = (A, B, C, D, E, F) be a relation schema with the following dependencies
C→ F, E→ A, EC→ D, A→ B. Which of the following is a key of R?
C→ F, E→ A, EC→ D, A→ B. Which of the following is a key of R?
CD | |
EC | |
AE | |
AC |
Question 20 Explanation:
Here, simple way to solve this question is,
First we have to find the right hand side values of a dependencies. Check whether it cover all variables in a relation .
In right hand side, CE are missing. It means definitely CE should be there in candidate key.
(CE)+=(A,B,C,D,E,F).
Remaining all are not satisfying candidate key properties.
First we have to find the right hand side values of a dependencies. Check whether it cover all variables in a relation .
In right hand side, CE are missing. It means definitely CE should be there in candidate key.
(CE)+=(A,B,C,D,E,F).
Remaining all are not satisfying candidate key properties.
There are 20 questions to complete.
