Nielit Scientific Assistance CS 15-10-2017
Question 1 |
A decimal has 25 digits. the number of bits needed for its equivalent binary representation is approximately
50 | |
74 | |
40 | |
None of the above |
Question 1 Explanation:
Consider three digits(1,2,3) of decimal numbers.Maximum number, we can generate by that three digits are 10 3 -1 which is 999.
Then, Decimal number has 25 digits, so maximum number is 10 25 -1
Similarly, in the binary representation with “n” bits the maximum number is 2 25 -1
So we can write 10 25 –1 = 2 n – 1 → 10 25 = 2 n
After taking log 2 on both sides
log 2 2 n =log 2 10 25
n log 2 2=25 log 2 10
n = 25 log 2 10
n = 25 x 3.3 [ log 2 2=1 & log 2 10 =3.322]
n = 82.5
Note: Original question paper given option D is 60. But actual answer is 82.5.
Then, Decimal number has 25 digits, so maximum number is 10 25 -1
Similarly, in the binary representation with “n” bits the maximum number is 2 25 -1
So we can write 10 25 –1 = 2 n – 1 → 10 25 = 2 n
After taking log 2 on both sides
log 2 2 n =log 2 10 25
n log 2 2=25 log 2 10
n = 25 log 2 10
n = 25 x 3.3 [ log 2 2=1 & log 2 10 =3.322]
n = 82.5
Note: Original question paper given option D is 60. But actual answer is 82.5.
Question 2 |
Which of the following is minimum error code?
Octal code | |
Binary Code | |
Gray code | |
Excess-3 Code |
Question 2 Explanation:
→ "Gray code" as an alternative name is "reflected binary code". one of those also lists "minimum error code" and "cyclic permutation code" among the names.
→ Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.
→ Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.
Question 3 |
Match list I with list II and select the correct answer using the codes given below the lists.



1 2 3 4 | |
3 2 4 1 | |
2 3 1 4 | |
1 4 2 3 |
Question 3 Explanation:
3 address instruction:
Two operand locations and a result location are explicitly contained in the instruction word.
e.g., Y = A − B
2 address instruction:
One of the addresses is used to specify both an operand and the result location.
e.g., Y = Y + X
1 address instruction:
Two addresses are implied in the instruction and accumulator based operations.
e.g., A CC = A CC + X
0 address instructions:
They are applicable to a special memory organization called a stack. It interact with a stack using push and pop operations. All addresses are implied as in register based operations.
T = Tap(T − 1 )
Two operand locations and a result location are explicitly contained in the instruction word.
e.g., Y = A − B
2 address instruction:
One of the addresses is used to specify both an operand and the result location.
e.g., Y = Y + X
1 address instruction:
Two addresses are implied in the instruction and accumulator based operations.
e.g., A CC = A CC + X
0 address instructions:
They are applicable to a special memory organization called a stack. It interact with a stack using push and pop operations. All addresses are implied as in register based operations.
T = Tap(T − 1 )
Question 4 |
A binary search tree contains the values- 1,2,3,4,5,6,7 and 8. The tree is traverses in preorder and the values are printed out. Which of the following sequences is a valid output?
5 3 1 2 4 7 8 6 | |
5 3 1 2 6 4 9 7 | |
5 3 2 4 1 6 7 8 | |
5 3 1 2 4 7 6 8 |
Question 4 Explanation:
Preorder traversal yields (Root, left, right)
Option D:
Let draw binary search tree for the given sequence,

After traversing through this tree we will get same sequence.
Option D:
Let draw binary search tree for the given sequence,
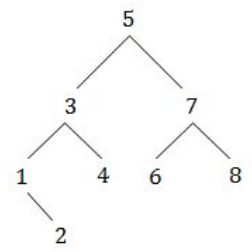
After traversing through this tree we will get same sequence.
Question 5 |
The number of the edges in a regular graph of degree 'd' and 'n' vertices is____
Maximum of n,d | |
n+d | |
nd | |
nd/2 |
Question 5 Explanation:
Sum of degree of vertices = 2*no. of edges
d*n = 2*|E|
∴ |E| = (d*n)/2
d*n = 2*|E|
∴ |E| = (d*n)/2
Question 6 |
Consider the following C code segment:
int IsPrime(n)
{
int i,n;
for(i=2;i<= √n;i++)
if(n%i == 0)
{
printf(“Not Prime\n”);
return 0;
}
return 1;
}
Let T(n) denotes the number of times the for loop is executed by the program on input n.
Which of the following is TRUE?
int IsPrime(n)
{
int i,n;
for(i=2;i<= √n;i++)
if(n%i == 0)
{
printf(“Not Prime\n”);
return 0;
}
return 1;
}
Let T(n) denotes the number of times the for loop is executed by the program on input n.
Which of the following is TRUE?
T(n) = O( √n) and T(n) = Ω ( √n) | |
T(n) = O( √n) and T(n) = Ω (1) | |
T(n) = O(n) and T(n) = Ω ( √n) | |
None of the above |
Question 6 Explanation:
Then the time complexity is Best Case : Ω(1) & Worst Case: O(√n)
Question 7 |
A language L for which there exists a TM,, 'T', that accepts every word in L and either rejects or loops for every word that is not in L, is said to be
recursive | |
recursively enumerable | |
NP-Hard | |
None of the above |
Question 7 Explanation:
A language L for which there exists a TM,, 'T', that accepts every word in L and either rejects or loops for every word that is not in L, is said to be recursively enumerable
Question 8 |
Synthesized attribute can easily be simulated by an
LL grammar | |
ambiguous grammar | |
LR grammar | |
none of the above |
Question 8 Explanation:
● A Synthesized attribute is an attribute of the nonterminal on the left-hand side of a production.
● Synthesized attributes represent information that is being passed up the parse tree.
● LR-attributed grammars allow the attributes to be evaluated on LR parsing. As a result, attribute evaluation in LR-attributed grammars can be incorporated conveniently in bottom-up parsing.
● Synthesized attributes represent information that is being passed up the parse tree.
● LR-attributed grammars allow the attributes to be evaluated on LR parsing. As a result, attribute evaluation in LR-attributed grammars can be incorporated conveniently in bottom-up parsing.
Question 9 |
The logic of pumping lemma us a good example of
The pigeonhole principle | |
The divide and conquer technique | |
recursion | |
Iteration |
Question 9 Explanation:
→ The pigeonhole principle is nothing more than the obvious remark: if you have fewer pigeon holes than pigeons and you put every pigeon in a pigeon hole, then there must result at least one pigeon hole with more than one pigeon. It is surprising how useful this can be as a proof strategy.
→ In the theory of formal languages in computability theory, a pumping lemma or pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of times, with the resulting string remaining in that language. The proofs of these lemmas typically require counting arguments such as the pigeonhole principle.
→ In the theory of formal languages in computability theory, a pumping lemma or pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of times, with the resulting string remaining in that language. The proofs of these lemmas typically require counting arguments such as the pigeonhole principle.
Question 10 |
Given relations R(w,x) and S(y,z) the result of
SELECT DISTINCT w,x from R<S
R has no duplicates and S is non empty | |
R and S have no duplicates | |
S has no duplicates and R is non empty | |
R and S has the same number of tuples |
Question 10 Explanation:
r has no duplicate, if r can have duplicates it can be remove in the final state. s in non-empty if s is empty then r*s becomes empty.
Question 11 |
E-R model uses this symbol to represent weak entity set?
Dotted rectangle | |
Diamond | |
Doubly outlined rectangle | |
None of these |
Question 11 Explanation:
→ A weak entity is an entity that cannot be uniquely identified by its attributes alone.
→ It must use a foreign key in conjunction with its attributes to create a primary key.
→ The foreign key is typically a primary key of an entity it is related to.

→ It must use a foreign key in conjunction with its attributes to create a primary key.
→ The foreign key is typically a primary key of an entity it is related to.
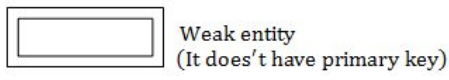
Question 12 |
By open domain CASE tools we mean
tools available in open domain | |
Software packages which can be downloaded from the internet | |
Software packages to aid each phase of the systems analysis and design which an be downloaded free of cost from the internet | |
Source codes of CASE tools |
Question 12 Explanation:
● Tools are also in the open domain which can be downloaded and used.
● They do not usually have very good user interfaces.
● They do not usually have very good user interfaces.
Question 13 |
If P is risk probability, L is loss, then is computed as
RE=P/L | |
RE=P+L | |
RE=P*L | |
RE=2*P*L |
Question 13 Explanation:
Risk Exposure(RE) is determined using the following relationship
RE = P*L
where P is the probability of occurrence for a risk, and L is the cost to the project should the risk occur.
where P is the probability of occurrence for a risk, and L is the cost to the project should the risk occur.
Question 14 |
A can is filled with 5 paise coins. Another can is filled with 10 paise coins. Another can is filled with 25 paise coins. All the cans are given wrong labels. If the can labeled 25 paise is not having the 10 paise coins, what will the can, labeled 10 paise have?
25 paise | |
5 paise | |
10 paise | |
cannot be determined |
Question 14 Explanation:
A diagram will make it easy to comprehend.

It is easy to find that the can labeled 25 Paise must have 5 paise coins in it. So, the can labeled 10 Paise, must have 25 Paise coins in it.

It is easy to find that the can labeled 25 Paise must have 5 paise coins in it. So, the can labeled 10 Paise, must have 25 Paise coins in it.
Question 15 |
The possible number of boolean function of 3 variables X,Y and Z such that f(X,Y,Z)=f(X',Y',Z')
8 | |
16 | |
64 | |
32 |
Question 15 Explanation:
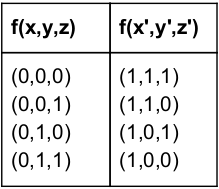
→ Like above other input combinations also repeat after these inputs.
→ We have 4 input pairs and produces output either 0 or 1.
→ Total functions possible=2*2*2*2 (or) 2 4 =16
There are 15 questions to complete.
Scientific Assistance CS 15-10-2017
Question 1 |
The difference between the compound interest and the simple earned at the end of 3 rd year on a sum of money at a rate of 10% per annul is Rs. 77.5. What is the sum?
Rs. 3,500 | |
Rs. 2,500 | |
Rs. 3,000 | |
Rs. 2,000 |
Question 1 Explanation:
Let principal be ‘x’
S.I = P T R / 100
S.I = X * 3 * 10 / 100
C.I = [ P (1 + (R / 100)T) - P]
C.I = [ X (1+ (10 / 100)3) - X]
C.I = 331X / 1000
Difference between Compound interest and Simple interest is 77.5
( 331X / 1000 ) - ( 3X / 10) = 77.5
31x / 1000 = 77.5
x = 2500.
S.I = P T R / 100
S.I = X * 3 * 10 / 100
C.I = [ P (1 + (R / 100)T) - P]
C.I = [ X (1+ (10 / 100)3) - X]
C.I = 331X / 1000
Difference between Compound interest and Simple interest is 77.5
( 331X / 1000 ) - ( 3X / 10) = 77.5
31x / 1000 = 77.5
x = 2500.
Question 2 |
Aamir and Birju can cut 5000g of wood in 20 min. Birju and Charles can cut 5000g of wood in 40 min. Charles and Aamir cut 5 kg of wood in 30 min. How much time Charles will take to cut 5 kg wood alone?
120 min | |
48 min | |
240 min | |
120 min |
Question 2 Explanation:
Here in this question 5000g means 5kg only
So from that question Aamir (A) Birju (B) Charles (C)
Let Aamir, Birju and Charles alone can complete the work in A, B and C minutes respectively, then
1 min. work of (A+B)=1/20, (B+C)=1/40 and (C+A)=1/30
A + B + C = 13/240
1 min. work of C = (A+B+C) - (A+B) = 13/240 - 1/20 = 1/240
So C alone can complete the work in 240 min.
So from that question Aamir (A) Birju (B) Charles (C)
Let Aamir, Birju and Charles alone can complete the work in A, B and C minutes respectively, then
1 min. work of (A+B)=1/20, (B+C)=1/40 and (C+A)=1/30
A + B + C = 13/240
1 min. work of C = (A+B+C) - (A+B) = 13/240 - 1/20 = 1/240
So C alone can complete the work in 240 min.
Question 3 |
An alloy contains copper and zinc in the ratio 5 : 3 and another contains copper and tin in the ratio 8 : 5, If equal weights of the two are melted together to form a 3 rd alloy, find the weight of tin per kg in the new alloy.
40/129 | |
5/13 | |
5/26 | |
28/5 |
Question 3 Explanation:
Amount of copper in first alloy is 5x/8 and zinc is 3x/8.
Amount of copper in second alloy is 8x/13 and tin is 5x/13.
So after mixing tin is available in 2 alloy only that means in 3rd alloy 5x/13/2x
Tin present in 3rd alloy is 5/26.
Amount of copper in second alloy is 8x/13 and tin is 5x/13.
So after mixing tin is available in 2 alloy only that means in 3rd alloy 5x/13/2x
Tin present in 3rd alloy is 5/26.
Question 4 |
X is a whole number. If the only common factors of X and X2 are 1 and X, then X is _______
1 | |
a perfect square | |
an odd number | |
a prime number |
Question 4 Explanation:
A number that is divisible only by itself and 1 is called prime number.
Question 5 |
Line AB is 24 metres in length and tangent to the inner one of the two concentric circles at point C, Points A and B lie on the circumference of the outer circle. It is known that the radii of the two circles are integers. The radius of the outer circle is
13m | |
5 m | |
7 m | |
4m |
Question 5 Explanation:

Given data,
AB=24cm
CB=12cm
θC=5cm(Assume)
θB=5 2 +12 2 =169
θB=13cm
Note: They forgot to mention the value 5. If we are considering value=5 then answer should be A.
Question 6 |
Monisha is working with a real estate agent to find a location for the kids’ toy store she plans to open in her town. She is looking for a place that is either in the centre or not too far from the centre of town. It should also be attractive for the right kind of footfall too. Which of the following locations should Monisha’s agent call to her attention?
a storefront in a new high-rise building near the train station in the center of town whose occupants are mainly young, childless professionals who use the train to commute to their offices each day | |
a little shop three blocks away from the town’s main street, located across the street from an elementary school and next door to an ice cream store | |
a stand-alone storefront on a quiet residential street ten blocks away from the town’s center | |
a storefront in a small a strip mall located on the outskirts of town that is also occupied by a pharmacy and a dry cleaner |
Question 6 Explanation:
This option is both near the center of town and in a location where children and their parents are sure to be around. This is the only option that meets both of Monisha’s requirements.
Question 7 |
Reading is a psycholinguistic guessing game. To read critically is a skill as it is a demanding process. One must slow down one’s reading and, with a pencil in hand, perform specific operations on the text. Mark up the text with reactions, conclusions and questions. When one reads, one becomes an active participant.
critical reading is a slow, dull, but essential process. | |
the best critical reading happens at critical times in a person’s life. | |
readers should get in the habit of questioning the truth of what they read. | |
critical reading requires thoughtful and careful attention |
Question 7 Explanation:
Option-A FALSE: The author never says that reading is dull.
Option-B,C FALSE: Not related to given paragraph.
Option-D TRUE: The author stresses the need to read critically by performing thoughtful and careful operations on the text.
Option-B,C FALSE: Not related to given paragraph.
Option-D TRUE: The author stresses the need to read critically by performing thoughtful and careful operations on the text.
Question 8 |
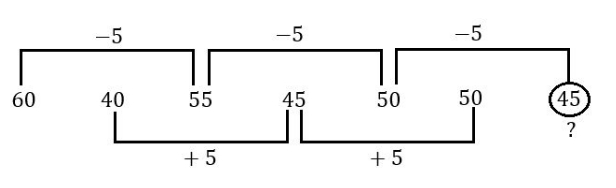
Find the missing term:
60, 40, 55, 45, 50, 50,?
60, 40, 55, 45, 50, 50,?
45 | |
50 | |
55 | |
60 |
Question 8 Explanation:
Question 9 |
Find the missing alphabet:
T, r, O, m, J,?
T, r, O, m, J,?
h | |
i | |
I | |
g |
Question 9 Explanation:
In between r and T there is letter is s
Likewise m and O letter is n
Same h is the next letter to fit in that sequence
Likewise m and O letter is n
Same h is the next letter to fit in that sequence
Question 10 |
Here are some words translated from an artificial language.
Qmelaqali means fruitcake
Qalitiimmeo means cakewalk
Useguamao means buttercup
Which word could mean “cupcake”?
Qmelaqali means fruitcake
Qalitiimmeo means cakewalk
Useguamao means buttercup
Which word could mean “cupcake”?
qalitiiqali | |
amaotiimmeo | |
pakitreft | |
amaoqali |
Question 10 Explanation:
Qmelaqali→ fruitcake
We can divide artificial language into parts.
Qmela→ fruit
qali→ cake
Qalitiimmeo→ cakewalk
We can divide artificial language into parts.
Qali→ cake
tiimmeo→ walk
Useguamao → buttercup
We can divide artificial language into parts.
Usegu→ butter
amao→ cup
cupcake→ ?
amao→ cup
qali→ cake
So, option-D is correct answer.
We can divide artificial language into parts.
Qmela→ fruit
qali→ cake
Qalitiimmeo→ cakewalk
We can divide artificial language into parts.
Qali→ cake
tiimmeo→ walk
Useguamao → buttercup
We can divide artificial language into parts.
Usegu→ butter
amao→ cup
cupcake→ ?
amao→ cup
qali→ cake
So, option-D is correct answer.
Question 11 |
A man walks 5 Km towards south and then turns to the right. After walking 3 Km he turns to the left and walks 5 Km. Now in which direction is he from the starting place?
West | |
South | |
North-East | |
South- West |
Question 11 Explanation:
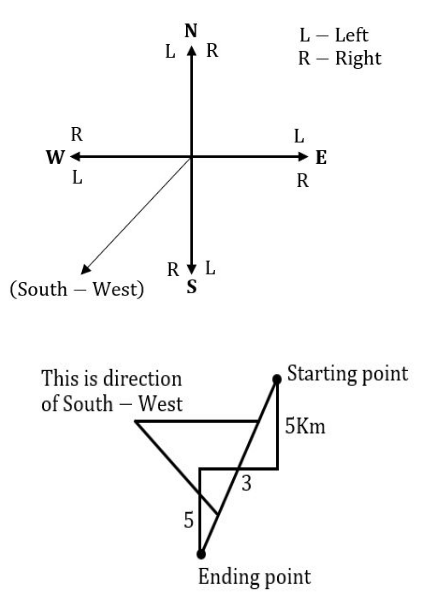
Question 12 |
If the consonants in the word ‘DROVE’ are first arranged alphabetically and the vowels are put in between two pairs of consonants in the alphabetical order, which of the following will be the fourth from the right end after the rearrangement?
D | |
E | |
R | |
O |
Question 12 Explanation:
In the word DROVE we have two vowels
Those are O and E
After consonants are arranged in alphabetically we got the word like DRV
But we have two place vowels in between two pairs of consonants we got finally DEROV
So right from fourth letter is E
Those are O and E
After consonants are arranged in alphabetically we got the word like DRV
But we have two place vowels in between two pairs of consonants we got finally DEROV
So right from fourth letter is E
Question 13 |
There is a queue in a ticketing office. Amanda is 10 th from the front while Murthy is 25 th from behind and Marta is just in the middle of the two. If there be 50 persons in the queue. What position does Marta occupy from the front?
16 | |
18 | |
15 | |
17 |
Question 13 Explanation:

Question 14 |
There are five janitors. Pali, Qureshi, Rohan, Sant and Timber. They all have a different height, Qureshi is shorter than only Timber and Sant is shorter than Pali and Qureshi. Who among them is the shortest?
Rohan | |
Sant | |
Pali | |
Data inadequate |
Question 14 Explanation:
From that question we can decide Pali Quereshi sant and timber but Rohan is not mentioned there. So Data inadequate is answer.
Question 15 |
A $ B means A is the father of B; A # B means A is the sister of B; A * B means A is the daughter of B and A @ B means A is the brother of B. Which of the following indicates that M is the wife of Q?
Q $ R # T @ M | |
Q $ R @ T # M | |
Q $ R * T # M | |
Q $ R @ T * M |
Question 15 Explanation:
Q $ R means R’s father is Q
R @ T means T’s brother is R
T * M means M’s Daughter T
Finally M’s Daughter is T and T’s Brother is R and R’s father is Q so Q’s wife is M.
R @ T means T’s brother is R
T * M means M’s Daughter T
Finally M’s Daughter is T and T’s Brother is R and R’s father is Q so Q’s wife is M.
There are 15 questions to complete.
