UGC NET CS 2014 Dec-Paper-2
Question 1 |
Consider a set A = {1, 2, 3, ........, 1000}. How many members of A shall be divisible by 3 or by 5 or by both 3 and 5 ?
533 | |
599 | |
467 | |
66 |
Question 1 Explanation:
Method-1:
Given data,
-- Set A={1, 2, 3, ........, 1000}
-- Set A shall be divisible by 3=?
-- Set A shall be divisible by 5=?
-- Set A shall be divisible by 3 and 5=?
Step-1: To find divisible by 3 numbers are
=⌊1000/3⌋
= 333
Step-2: To find divisible by 5 numbers are
=⌊1000/5⌋
= 200
Step-3: To find divisible by 3 and 5 numbers are
=⌊1000/(3*5)⌋
= 66
These 66 is already part of 333 and 200. So, we have to exclude it from the list.
Total= 333+200-66
= 467
Note: We are using floor because excluding fraction value.
Method-2:
The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467
Note: Getting this idea in exam hall is very difficult. So, better follow method-1 ratherhan method-2
Given data,
-- Set A={1, 2, 3, ........, 1000}
-- Set A shall be divisible by 3=?
-- Set A shall be divisible by 5=?
-- Set A shall be divisible by 3 and 5=?
Step-1: To find divisible by 3 numbers are
=⌊1000/3⌋
= 333
Step-2: To find divisible by 5 numbers are
=⌊1000/5⌋
= 200
Step-3: To find divisible by 3 and 5 numbers are
=⌊1000/(3*5)⌋
= 66
These 66 is already part of 333 and 200. So, we have to exclude it from the list.
Total= 333+200-66
= 467
Note: We are using floor because excluding fraction value.
Method-2:
The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467
Note: Getting this idea in exam hall is very difficult. So, better follow method-1 ratherhan method-2
Question 2 |
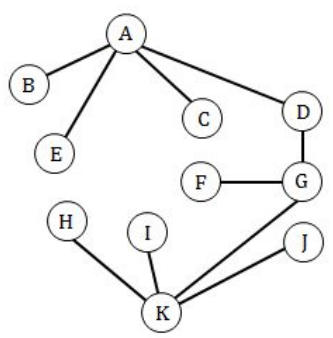
A certain tree has two vertices of degree 4, one vertex of degree 3 and one vertex of degree 2. If the other vertices have degree 1, how many vertices are there in the graph ?
5 | |
n-3 | |
20 | |
11 |
Question 2 Explanation:
Method-1:
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees

B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees
B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Question 3 |
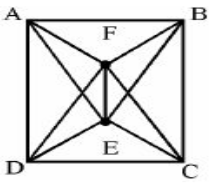
Consider the Graph shown below :

This graph is a __________.
This graph is a __________.
Complete Graph | |
Bipartite Graph | |
Hamiltonian Graph | |
All of the above |
Question 3 Explanation:
Option-A: It is not complete graph because it won’t have n(n-1)/2 edges.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once.

Hence, Option-C is correct answer.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once.
Hence, Option-C is correct answer.
Question 4 |
A computer program selects an integer in the set {k : 1 ≤ k ≤ 10,00,000} at random and prints out the result. This process is repeated 1 million times. What is the probability that the value k=1 appears in the printout at least once ?
0.5 | |
0.704 | |
0.632121 | |
0.68 |
Question 4 Explanation:
Probability that the value k=1 appears in the printout at least once is
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121
Hence answer is option C
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121
Hence answer is option C
Question 5 |
If we define the functions f, g and h that map R into R by :
f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72, then the value of the composite functions ho(gof) and (hog)of are given as
x 8 – 71 and x 8 – 71 | |
x 8 – 73 and x8 – 73 | |
x 8 + 71 and x 8 + 71 | |
x 8 + 73 and x 8 + 73 |
Question 5 Explanation:
Given f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73
Hence, option-D is the correct answer
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73
Hence, option-D is the correct answer
Question 6 |
The BCD adder to add two decimal digits needs minimum of
6 full adders and 2 half adders | |
5 full adders and 3 half adders | |
4 full adders and 3 half adders | |
5 full adders and 2 half adders |
Question 6 Explanation:
→ Each digit is represented by a 4-bit BCD code.
→ To add two 4-bit number, we need 1 Half Adder(to add LSBs) and 3 Full Adders(remaining three bits of both number along with carry bits).
→ To make the resultant Sum as valid BCD sum, we need to add 0110 to the sum.
→ This can be done with 1 Half adder and 2 Full Adder
(Note: LSB bit of 0110 is always zero. So there is no need of ADDER to add LSBs.)
→ Here, Half adder is used to add next significant bits.
Total 5 Full Adders and 2 Half Adders are needed
→ To add two 4-bit number, we need 1 Half Adder(to add LSBs) and 3 Full Adders(remaining three bits of both number along with carry bits).
→ To make the resultant Sum as valid BCD sum, we need to add 0110 to the sum.
→ This can be done with 1 Half adder and 2 Full Adder
(Note: LSB bit of 0110 is always zero. So there is no need of ADDER to add LSBs.)
→ Here, Half adder is used to add next significant bits.
Total 5 Full Adders and 2 Half Adders are needed
Question 7 |
The Excess-3 decimal code is a self-complementing code because
The binary sum of a code and its 9’s complement is equal to 9. | |
It is a weighted code | |
Complement can be generated by inverting each bit pattern | |
The binary sum of a code and its 10’s complement is equal to 9 |
Question 7 Explanation:
The Excess-3 decimal code is a self-complementing code because complement can be generated by inverting each bit pattern.

Question 8 |
How many PUSH and POP operations will be needed to evaluate the following expression by reverse polish notation in a stack machine (A * B) + (C * D/E) ?
4 PUSH and 3 POP instructions | |
5 PUSH and 4 POP instructions | |
6 PUSH and 2 POP instructions | |
5 PUSH and 3 POP instructions |
Question 8 Explanation:
Given infix notation, we have to change infix notation into postfix notation.
after converting postfix notation the notations are ab* cde /* +

Total 5 PUSH and 4 POP operations performed.
after converting postfix notation the notations are ab* cde /* +

Total 5 PUSH and 4 POP operations performed.
Question 9 |
The range of representable normalized numbers in the floating point binary fractional representation in a 32-bit word with 1-bit sign, 8-bit excess 128 biased exponent and 23-bit mantissa is
2 -128 to (1 – 2 –23 ) * 2 127 | |
(1 – 2 –23 ) * 2 -127 to 2 128 | |
(1 – 2 –23 ) * 2 –127 to 2 23> | |
2 –129 to (1 – 2 –23 ) * 2 127 |
Question 9 Explanation:
The range of representable normalized numbers in the floating point binary fractional representation in a 32-bit word with 1-bit sign, 8-bit excess 128 biased exponent and 23-bit mantissa is 2 –129 to (1 – 2 –23 ) * 2 127
Question 10 |
The size of the ROM required to build an 8-bit adder/subtractor with mode control, carry input, carry output and two’s complement overflow output is given as
2 16 * 8 | |
2 18 * 10 | |
2 16 * 10 | |
2 18 * 8 |
Question 10 Explanation:
The size of the ROM required to build an 8-bit adder/subtractor with mode control, carry input, carry output and two’s complement overflow output is given as 2 18 * 10.
Question 11 |
What will be the output of the following ‘C’ code ?
main( )
{
int x=128;
printf (“\n%d”, 1 + x++);
}
main( )
{
int x=128;
printf (“\n%d”, 1 + x++);
}
128 | |
129 | |
130 | |
131 |
Question 11 Explanation:
In this program we are using post increment. Post increment will send the value before updating the value.
printf(“\n%d”, 1 + x++); /* x=128 */
Here, 1+128=129
printf(“\n%d”, 1 + x++); /* x=128 */
Here, 1+128=129
Question 12 |
What does the following expression means ?
char *(*(*a[N]) ( )) ( );
a pointer to a function returning array of n pointers to function returning character pointers. | |
a function return array of N pointers to functions returning pointers to characters | |
an array of n pointers to function returning pointers to characters | |
an array of n pointers to function returning pointers to functions returning pointers to characters. |
Question 12 Explanation:
char *(*(*a[N]) ( )) ( ); /* an array of n pointers to function returning pointers to functions returning pointers to characters */
There are 12 questions to complete.
