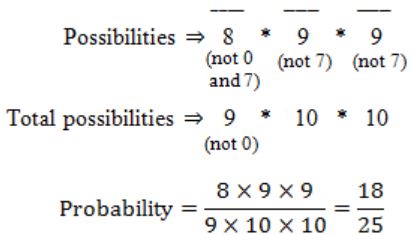GATE 1995

Question 1

A single instruction to clear the lower four bits of the accumulator in 8085 assembly language?

A
XRI OFH
B
ANI FOH
C
XRI FOH
D
ANI OFH
Computer-OrganizationMicroprocessor
Question 1 Explanation: 
Here, we use the AND as a accumulator with immediate. F leaves the high nibble whatever it is, 0 clears the lower nibble.
→ The XOR's don't reliably clear random bits and ANI OF clears the upper nibble, not the lower nibble.
Question 2

Which of the following statements is true?

A
ROM is a Read/Write memory
B
PC points to the last instruction that was executed
C
Stack works on the principle of LIFO
D
All instructions affect the flags
Operating-SystemsGeneral
Question 2 Explanation: 
We know that stack works on the principle of LIFO.
Question 3

In a vectored interrupt

A
the branch address is assigned to a fixed location in memory
B
the interrupt source supplies the branch information to the processor through an interrupt vector
C
the branch address is obtained from a register in the processor
D
none of the above
Computer-OrganizationInterrupt
Question 3 Explanation: 
A vectored interrupt is a processing technique in which the interrupting device directs the processor to the appropriate interrupt service routine vector.
Question 4

In the following Pascal program segment, what is the value of X after the execution of the program segment?
X:=-10; Y:=20;
If X > Y then if X < 0 then X:=abs(X) else X:=2*X;

A
10
B
-20
C
-10
D
None
ProgrammingPASCAL-Programming
Question 4 Explanation: 
X is remains unchanged. As the if condition is becomes false.
X = -10
Question 5

Merge sort uses

A
Divide and conquer strategy
B
Backtracking approach
C
Heuristic search
D
Greedy approach
AlgorithmsSorting
Question 5 Explanation: 
Merge sort uses the divide and conquer strategy.
Question 6

The principle of locality justifies the use of

A
interrupts
B
DMA
C
Polling
D
Cache Memory
Computer-OrganizationGeneral
Question 6 Explanation: 
The locality of reference is also known as principle of locality.
→ The things which are used more frequently those are stored in locality of reference.
→ For this purpose we use the cache memory.
Question 7

In a paged segmented scheme of memory management, the segment table itself must have a page table because

A
the segment table is often too large to fit in one page
B
each segment is spread over a number of pages
C
segment tables point to page table and not to the physical locations of the segment
D
the processor’s description base register points to a page table
E
Both A and B
Operating-SystemsMemory-Management
Question 7 Explanation: 
The segment table is often too large to fit in one page. This is true and the segment table can be divided into pages. Thus page table for each segment table, pages are created.
Segment paging is different from paged segmentation.
Question 8

Which of the following page replacement algorithms suffers from Belady’s anamoly?

A
Optimal replacement
B
LRU
C
FIFO
D
Both (A) and (C)
Operating-SystemsPage-Replacement-Algorithm
Question 8 Explanation: 
FIFO is suffers from Belady's Anamoly.
Question 9

In some programming languages, an identifier is permitted to be a letter following by any number of letters or digits. If L and D denote the sets of letters and digits respectively, which of the following expressions defines an identifier?

A
(L ∪ D)+
B
L(L ∪ D)*
C
(L⋅D)*
D
L⋅(L⋅D)*
Theory-of-ComputationRegular-Expression
Question 9 Explanation: 
Which is to be letter followed by any number of letters (or) digits
L(L ∪ D)*
Question 10

Consider a grammar with the following productions

S → a∝b|b∝c| aB
S → ∝S|b
S → ∝b b|ab
S ∝ → bd b|b

The above grammar is:

A
Context free
B
Regular
C
Context sensitive
D
LR(k)
Theory-of-ComputationGeneral
Question 10 Explanation: 
S ∝→ [violates context free]
Because LHS must be single non-terminal symbol.
S ∝→ b [violates CSG]
→ Length of RHS production must be atleast same as that of LHS.
Extra information is added to the state by redefining iteams to include a terminal symbol as second component in this type of grammar.
Ex: [A → αβa]
A → αβ is a production, a is a terminal (or) right end marker $, such an object is called LR(k).
So, answer is (D) i.e., LR(k).
Question 11

What are x and y in the following macro definition?

 macro Add x,y
 Load y
 Mul x
 Store y
 end macro
A
Variables
B
Identifiers
C
Actual parameters
D
Formal parameters
Computer-OrganizationMicroprocessor
Question 11 Explanation: 
Formal arguments (or) formal parameters is a special kind of variables used in subroutine to refer to one of pieces of data provided as input to the subroutine.
Question 12

What is the distance of the following code 000000, 010101, 000111, 011001, 111111?

A
2
B
3
C
4
D
1
Computer-NetworksError-Detection
Question 12 Explanation: 
Distance = Minimum hamming distance = 2
010101 ⊕ 011001 = 001100
Question 13

Which of the following strings can definitely be said to be tokens without looking at the next input character while compiling a Pascal program? 

 I. begin           II. program           III. <>
A
I
B
II
C
III
D
All of the above
ProgrammingPASCAL-Programming
Question 13 Explanation: 
Note: Out of syllabus.
Question 14

A linker is given object modules for a set of programs that were compiled separately. What information need to be included in an object module?

A
Object code
B
Relocation bits
C
Names and locations of all external symbols defined in the object module
D
Absolute addresses of internal symbols
Compiler-DesignRun-Time-Environment
Question 14 Explanation: 
In object module it includes names and locations of all external symbols defined in the object module.
To link to external symbols it must know the location of external symbols.
Question 15

Which scheduling policy is most suitable for a time shared operating system?

A
Shortest Job First
B
Round Robin
C
First Come First Serve
D
Elevator
Operating-SystemsCPU-Scheduling
Question 15 Explanation: 
In Round robin, we use the time quantum based on this execution can be done. Then it is said to be time shared operating system.
Question 16

For merging two sorted lists of sizes m and n into a sorted list of size m+n, we required comparisons of

A
O(m)
B
O(n)
C
O(m+n)
D
O(logm+logn)
Question 16 Explanation: 
In best case, no. of comparisons is Min(m,n).
In worst case, no. of comparisons is m+n-1.
Then we require O(m+n) comparisons to merging two sorted lists.
Question 17

A binary tree T has n leaf nodes. The number of nodes of degree 2 in T is:

A
log2 n
B
n - 1
C
n
D
2n
Question 17 Explanation: 
A binary tree is a tree data structure in which each node has atmost two child nodes.
The no. of subtrees of a node is called the degree of the node. In a binary tree, all nodes have degree 0, 1 and 2.
The degree of a tree is the maximum degree of a node in the tree. A binary tree is of degree 2.
The number of nodes of degree 2 in T is "n - 1".
Question 18

The probability that a number selected at random between 100 and 999 (both inclusive) will not contain the digit 7 is:

A
16/25
B
(9/10)3
C
27/75
D
18/25
Engineering-MathematicsProbability
Question 18 Explanation: 
There are 18 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access