GATE 1998
Question 1 |
A die is rolled three times. The probability that exactly one odd number turns up among the three outcomes is
1/6 | |
3/8 | |
1/8 | |
1/2 |
Total no. of possibilities are 8.
Probability of getting exactly one odd = 3/8
Question 2 |
Consider the following set of equations
x + 2y = 5
4x + 8y = 12
3x + 6y + 3z = 15 This set
has unique solution | |
has no solutions | |
has finite number of solutions | |
has infinite number of solutions |

Question 3 |
Which of the following statements applies to the bisection method used for finding roots of functions:
converges within a few iterations | |
guaranteed to work for all continuous functions | |
is faster than the Newton-Raphson method | |
requires that there be no error in determining the sign of the function
|
Question 4 |
Consider the function y = |x| in the interval [-1,1]. In this interval, the function is
continuous and differentiable | |
continuous but not differentiable | |
differentiable but not continuous | |
neither continuous nor differentiable |
→ The left side values of x=0 be negative and right side values are positive.
→ If the function is said to be differentiable then left side and right side values are to be same.
Question 5 |
What is the converse of the following assertion?
I stay only if you go.
I stay if you go | |
If I stay then you go | |
If you do not go then I do not stay | |
If I do not stay then you go |
⇒ i.e., A→B
Where A = If I stay; B = you go
Converse for (A→B) is (B→A)
⇒ If you go then I stay.
Question 6 |
Suppose A is a finite set with n elements. The number of elements in the largest equivalence relation of A is
n | |
n2 | |
1 | |
n+1 |
⇒ n×n
⇒ n2
Question 7 |
Let R1 and R2 be two equivalence relations on a set. Consider the following assertions:
- (i) R1 ∪ R2 is an equivalence relation
(ii) R1 ∩ R2 is an equivalence relation
Which of the following is correct?
Both assertions are true | |
Assertion (i) is true but assertion (ii) is not true | |
Assertion (ii) is true but assertion (i) is not true | |
Neither (i) nor (ii) is true |
(i) R1 ∩ R2 is also transitive.
(ii) R1 ∪ R2 is need not to be transitive.
Question 8 |
The number of functions from an m element set to an n element set is
m + n | |
mn | |
nm | |
m*n |
n×n×n×n×...×n (m times)
= nm
Question 9 |
If the regular set A is represented by A = (01 + 1)* and the regular set ‘B’ is represented by B = ((01)*1*)*, which of the following is true?
A ⊂ B | |
B ⊂ A | |
A and B are incomparable | |
A = B |
Question 10 |
Both A and B are equal, which generates strings over {0,1}, while 0 is followed by 1.
The numbers 1, 2, 4, 8, ……………., 2n, ………… written in binary | |
The numbers 1, 2, 4, ………………., 2n, …………..written in unary | |
The set of binary string in which the number of zeros is the same as the number of ones | |
The set {1, 101, 11011, 1110111, ………..} |
10, 100, 1000, 10000 .... = 10*
which is regular and recognized by deterministic finite automata.
Question 11 |
Regarding the power of recognition of languages, which of the following statements is false?
The non-deterministic finite-state automata are equivalent to deterministic finite-state automata. | |
Non-deterministic Push-down automata are equivalent to deterministic Push- down automata. | |
Non-deterministic Turing machines are equivalent to deterministic Push-down automata. | |
Both B and C |
C: Power (TM) > NPDA > DPDA.
Question 12 |
The string 1101 does not belong to the set represented by
110*(0 + 1) | |
1 ( 0 + 1)* 101 | |
(10)* (01)* (00 + 11)* | |
Both C and D |
C & D are not generate string 1101.
Question 13 |
What happens when a bit-string is XORed with itself n-times as shown:
[B⊕(B⊕(B⊕(B........ n times)]
complements when n is even | |
complements when n is odd | |
divides by 2n always | |
remains unchanged when n is even |
Consider:
B⊕(B⊕B)
= B⊕0
= 0 (if consider n times it remains unchanged)
Question 14 |
A multiplexor with a 4 bit data select input is a
4:1 multiplexor | |
2:1 multiplexor | |
16:1 multiplexor | |
8:1 multiplexor |
For 4 bit data it selects 24 : 1 = 16: 1 input
Question 15 |
The threshold level for logic 1 in the TTL family is
any voltage above 2.5 V | |
any voltage between 0.8 V and 5.0 V | |
any voltage below 5.0 V | |
any voltage below Vcc but above 2.8 V |
Question 16 |
In serial communication employing 8 data bits, a parity bit and 2 stop bits, the minimum band rate required to sustain a transfer rate of 300 characters per second is
2400 band | |
19200 band | |
4800 band | |
1200 band |
(8+2+1+1) * 300
= 3600
Minimum band rate required is 4800 band.
Question 17 |
The octal representation of an integer is (342)8. If this were to be treated as an eight-bit integer is an 8085 based computer, its decimal equivalent is
226 | |
-98 | |
76 | |
-30 |
If this can be treated as 8 bit integer, then the first becomes sign bit i.e., '1' then the number is negative.
8085 uses 2's complement then
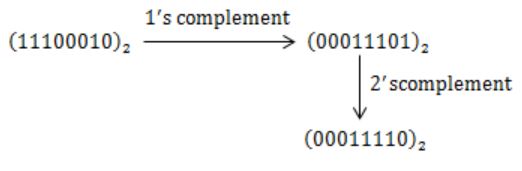
⇒ -30
Question 18 |
Which of the following devices should get higher priority in assigning interrupts?
Hard disk | |
Printer | |
Keyboard | |
Floppy disk |
Question 19 |
Which of the following addressing modes permits relocation without any change whatsoever in the code?
Indirect addressing | |
Indexed addressing | |
Base register addressing | |
PC relative addressing |
Question 20 |
Which of the following is true?
Unless enabled, a CPU will not be able to process interrupts. | |
Loop instructions cannot be interrupted till they complete. | |
A processor checks for interrupts before executing a new instruction. | |
Only level triggered interrupts are possible on microprocessors. |
Option 'C' also false. A processor checks for the interrupt before fetching an instruction.
