GATE 2006
Question 1 |
Consider the polynomial p(x) = a0 + a1x + a2x2 + a3x3, where ai ≠ 0, ∀i. The minimum number of multiplications needed to evaluate p on an input x is:
3 | |
4 | |
6 | |
9 |
p(x) = a0 + a1x + a2x2 + a3x3 where ai≠0
This can be written as
p(x) = a0 +x( a1 + a2x + a3x2)=a0+(a1+(a2+a3x)x)x
Total no. of multiplications required is 3
i.e., a3x = K.....(i)
(a2+K)x = M..... (ii)
(a1+M)x=N...... (iii)
Question 2 |
Let X, Y, Z be sets of sizes x, y and z respectively. Let W = X×Y and E be the set of all subsets of W. The number of functions from Z to E is:
Z2xy | |
Z×2xy | |
Z2x+y | |
2xyz |
A set ‘P’ consists of m elements and ‘Q’ consists of n elements then total number of function from P to Q is mn.
⇒ E be the no. of subsets of W = 2|w| = 2|xxy| = 2xy
No. of function from Z to E is = (2xy)z = (2xy)z = 2xyz
Question 3 |
The set {1, 2, 3, 5, 7, 8, 9} under multiplication modulo 10 is not a group. Given below are four plausible reasons. Which one of them is false?
It is not closed | |
2 does not have an inverse | |
3 does not have an inverse | |
8 does not have an inverse |
Option A:
It is not closed under multiplication. After multiplication modulo (10) we get ‘0’. The ‘0’ is not present in the set.
(2*5)%10 ⇒ 10%10 = 0
Option B:
2 does not have an inverse such as
(2*x)%10 ≠ 1
Option C:
3 have an inverse such that
(3*7)%10 = 1
Option D:
8 does not have an inverse such that
(8*x)%10 ≠ 1
Question 4 |
A relation R is defined on ordered pairs of integers as follows: (x,y) R(u,v) if x < u and y > v. Then R is: Then R is:
Neither a Partial Order nor an Equivalence Relation | |
A Partial Order but not a Total Order | |
A Total Order | |
An Equivalence Relation |
i) Symmetric
ii) Reflexive
iii) Transitive
If a relation is partial order relation then it must be
i) Reflexive
ii) Anti-symmetric
iii) Transitive
If a relation is total order relation then it must be
i) Reflexive
ii) Symmetric
iii) Transitive
iv) Comparability
Given ordered pairs are (x,y)R(u,v) if (x
Here <, > are using while using these symbol between (x,y) and (y,v) then they are not satisfy the reflexive relation. If they uses (x<=u) and (y>=u) then reflexive relation can satisfies.
So, given relation cannot be a Equivalence. Total order relation or partial order relation.
Question 5 |
For which one of the following reasons does Internet Protocol (IP) use the time-to- live (TTL) field in the IP datagram header?
Ensure packets reach destination within that time | |
Discard packets that reach later than that time | |
Prevent packets from looping indefinitely | |
Limit the time for which a packet gets queued in intermediate routers |
Question 6 |
Consider three CPU-intensive processes, which require 10, 20 and 30 time units and arrive at times 0, 2 and 6, respectively. How many context switches are needed if the operating system implements a shortest remaining time first scheduling algorithm? Do not count the context switches at time zero and at the end.
1 | |
2 | |
3 | |
4 |
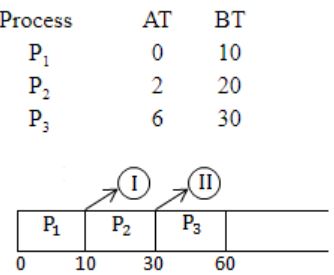
Total no.of context switches is 2.
Question 7 |
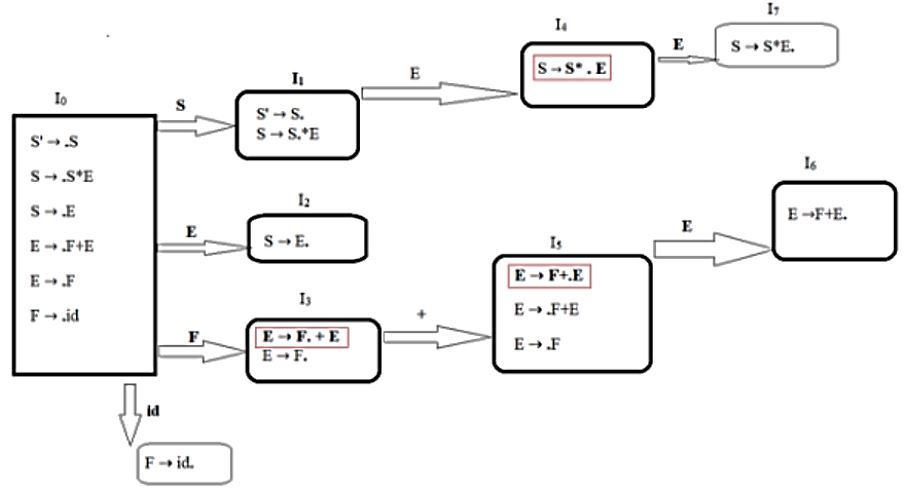
Consider the following grammar.
S → S * E S → E E → F + E E → F F → id
Consider the following LR(0) items corresponding to the grammar above.
(i) S → S * .E (ii) E → F. + E (iii) E → F + .E
Given the items above, which two of them will appear in the same set in the canonical sets-of-items for the grammar?
(i) and (ii) | |
(ii) and (iii) | |
(i) and (iii) | |
None of the above |
Question 8 |
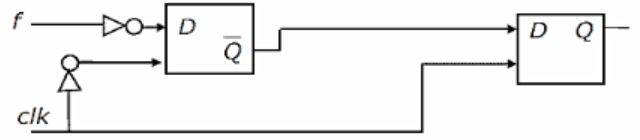
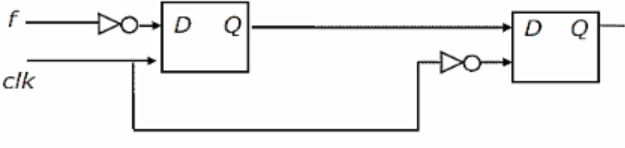
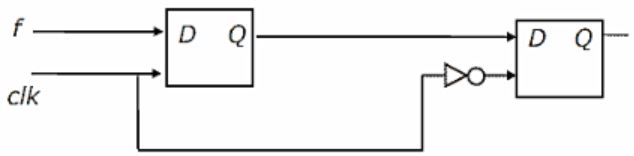
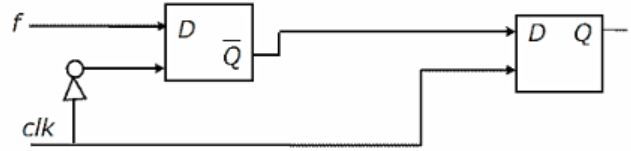
You are given a free running clock with a duty cycle of 50% and a digital waveform f which changes only at the negative edge of the clock. Which one of the following circuits (using clocked D flip-flops) will delay the phase of f by 180°?
 | |
 | |
 | |
 |
50% of duty cycle means, the wave is 1 for half of the time and 0 for the other half of the time. It is a usual digital signal with 1 and 0.
The waveform f changes for every negative edge, that means f value alters from 1 to 0 or 0 to 1 for every negative edge of the clock.
Now the problem is that we need to find the circuit which produces a phase shift of 180, which means the output is 0 when f is 1 and output is 1 when f is 0.
Like the below image.
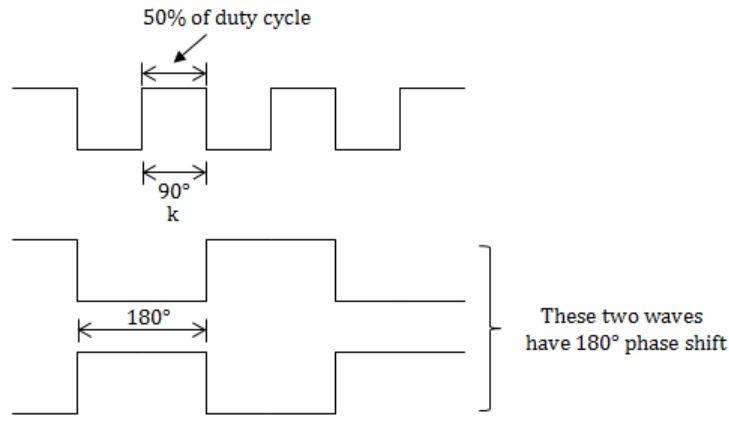
Now to find the answer we can choose elimination method.
F changes for negative edge, so that output too should change at negative edge. i.e if f becomes 0, then at the same time output should become 1, vice versa.
So, whenever input changes, at the same point of time output too should change. As input changes on negative edge, the output should be changed at negative edge only.
To have the above behaviour, the second D flip-flop which produces the final output should be negative edge triggered. because whatever the 2nd flip-flop produces, that is the output of the complete circuit.
So, we can eliminate option a, d.
Now either b or c can be answer.
How the flip-flop chain works in option b and c is as below.
—> F changes at negative edge.
—> But flip-flop1 responds at next positive edge.
—> After this flip-flop2 responds at next negative edge.
That means flip-flop2 produces the same input which is given to flip-flop now after a positive edge and a negative edge, that means a delay of one clock cycle, which is 180 degrees phase shift for the waveform of f.
Option b) we are giving f’, so that the output is f’ with 180 degrees phase shift.
Option c) we are giving f, so that the output is f with 180 degrees phase shift.
Hence option C is the answer.
Question 9 |
A CPU has 24-bit instructions. A program starts at address 300 (in decimal). Which one of the following is a legal program counter (all values in decimal)?
400 | |
500 | |
600 | |
700 |
So finally we can say that the values in the program counter will always be the multiple of 3.
Hence, option (C) is correct.
Question 10 |
In a binary max heap containing n numbers, the smallest element can be found in time
O(n) | |
O(log n) | |
O(log log n) | |
O(1) |
We have to search all the elements to reach the smallest element and heap using linear search.
To traverse all elements using linear search will take O(n) time.
Question 11 |
n-1 | |
2n-2 | |
 | |
n2 |
2) Weight of the minimum spanning tree = 2|2 - 1| + 2|3 - 2| + 2|4 - 3| + 2|5 - 4| .... + 2| n - (n-1) | = 2n - 2
Question 12 |
To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:
Queue | |
Stack | |
Heap | |
B-Tree |
Question 13 |
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. The root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i+1]. To be able to store any binary tree on n vertices the minimum size of X should be.
log2n | |
n | |
2n+1 | |
2n-1 |
Note: Assume level numbers are start with 0.
Question 14 |
Which one of the following in place sorting algorithms needs the minimum number of swaps?
Quick sort | |
Insertion sort | |
Selection sort | |
Heap sort |
Question 15 |
Consider the following C-program fragment in which i, j and n are integer variables.
for (i = n, j = 0; i >0; i /= 2, j += i);
Let val(j) denote the value stored in the variable j after termination of the for loop. Which one of the following is true?
val(j) = θ(logn) | |
val(j) = θ(√n) | |
val(j) = θ(n) | |
val(j) = θ(n logn) |
Question 16 |
Let S be an NP-complete problem and Q and R be two other problems not known to be in NP. Q is polynomial time reducible to S and S is polynomial-time reducible to R. Which one of the following statements is true?
R is NP-complete | |
R is NP-hard | |
Q is NP-complete | |
Q is NP-hard |
Question 17 |
An element in an array X is called a leader if it is greater than all elements to the right of it in X. The best algorithm to find all leaders in an array
Solves it in linear time using a left to right pass of the array | |
Solves it in linear time using a right to left pass of the array | |
Solves it using divide and conquer in time θ(nlogn) | |
Solves it in time θ(n2) |
Question 18 |
We are given a set X = {x1, .... xn} where xi = 2i. A sample S ⊆ X is drawn by selecting each xi independently with probability pi = 1/2. The expected value of the smallest number in sample S is:
1/n | |
2 | |
√n | |
n |
The given probability Pi is for selection of each item independently with probability 1/2.
Now, Probability for x1 to be smallest in S = 1/2
Now, Probability for x2 to be smallest in S = Probability of x1 not being in S × Probability of x2 being in S
= 1/2 × 1/2
Similarly, Probability xi to be smallest = (1/2)i
Now the Expected value is
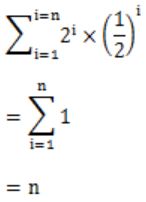
Question 19 |
Let L1 = {0n+m1n0m|n,m ≥ 0}, L2 = {0n+m1n+m0m|n,m ≥ 0}, and L3 = {0n+m1n+m0n+m|n,m ≥ 0}. Which of these languages are NOT context free?
L1 only | |
L3 only | |
L1 and L2 | |
L2 and L3 |
But for L2 and L3 PDA implementation is not possible. The reason is, in L2 there are two comparison at a time, first the number of 0’s in beginning should be equal to 1’s and then 0’s after 1’s must be less than or equal to number of 1’s. Suppose for initial 0’s and 1’s are matched by using stack then after matching stack will become empty and then we cannot determine the later 0’s are equal to or less than number of 1’s. Hence PDA implementation is not possible. Similarly L3 also has the similar reason.
Question 20 |
Consider the following log sequence of two transactions on a bank account, with initial balance 12000, that transfer 2000 to a mortgage payment and then apply a 5% interest.
1. T1 start
2. T1 B old=12000 new=10000
3. T1 M old=0 new=2000
4. T1 commit
5. T2 start
6. T2 B old=10000 new=10500
7. T2 commit
Suppose the database system crashes just before log record 7 is written. When the system is restarted, which one statement is true of the recovery procedure?
We must redo log record 6 to set B to 10500.
| |
We must undo log record 6 to set B to 10000 and then redo log records 2 and 3.
| |
We need not redo log records 2 and 3 because transaction T1 has committed.
| |
We can apply redo and undo operations in arbitrary order because they are idempotent. |
So from above theory we can say that option (B) is the correct answer.
Question 21 |
For each element in a set of size 2n, an unbiased coin is tossed. The 2n coin tosses are independent. An element is chosen if the corresponding coin toss were head. The probability that exactly n elements are chosen is:
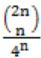 | |
 | |
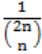 | |
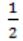 |
No. of elements selected = n
Probability of getting head = ½
Probability of n heads out of 2n coin tosses is
2nCn*(1/2)n*(1/2)n = 2nCn/4n
