ISRO CS 2020
Question 1 |
An array of two byte integers is stored in big endian machine in byte addresses as shown below. What will be its storage pattern in little endian machine?
Address Data
0 X 104 78
0 X 103 56
0 X 102 34
0 X 101 12
Address Data
0 X 104 78
0 X 103 56
0 X 102 34
0 X 101 12
0 X 104 12 0 X 103 56 0 X 102 34 0 X 101 12 | |
0 X 104 12 0 X 103 34 0 X 102 56 0 X 101 78 | |
0 X 104 56 0 X 103 78 0 X 102 12 0 X 101 34 | |
0 X 104 56 0 X 103 12 0 X 102 78 0 X 101 34 |
Question 1 Explanation:
In little endian the LSB parts of the data are stored first, whereas in big endian the MSB parts are stored first.
In the given question each integer is two bytes. 0x101, 0x102 are part of one word.
In the big endian 0x101 has 12 and 0x102 has 34. In the little endian 0x101 will have 34 and 0x102 will have 12.
Similarly in the big endian 0x103 has 56 and 0x104 has 78...in the little endian 0x103 will have 78 and 0x104 will have 56.
In the given question each integer is two bytes. 0x101, 0x102 are part of one word.
In the big endian 0x101 has 12 and 0x102 has 34. In the little endian 0x101 will have 34 and 0x102 will have 12.
Similarly in the big endian 0x103 has 56 and 0x104 has 78...in the little endian 0x103 will have 78 and 0x104 will have 56.
Question 2 |
A non-pipelined CPU has 12 general purpose registers(R0, R1, R2,........R12). Following operations are supported
ADD Ra, Rb, Rr Add Ra to Rb and store the result in Rr
MUL Ra, Rb, Rr Multiply Ra to Rb and store the result in Rr
MUL operations takes two clock cycles, ADD takes one clock cycle.
Calculate the minimum number of clock cycles required to compute the value of the expression XY+XYZ+YZ. The variables X, Y, Z are initially available in registers R0, R1 and R2 contents of these registers must not be modified.
ADD Ra, Rb, Rr Add Ra to Rb and store the result in Rr
MUL Ra, Rb, Rr Multiply Ra to Rb and store the result in Rr
MUL operations takes two clock cycles, ADD takes one clock cycle.
Calculate the minimum number of clock cycles required to compute the value of the expression XY+XYZ+YZ. The variables X, Y, Z are initially available in registers R0, R1 and R2 contents of these registers must not be modified.
5 | |
6 | |
7 | |
8 |
Question 2 Explanation:
To calculate XY+XYZ+YZ, we need at least 3 multiplication operations and 2 ADD operations.
Assuming R0 = X, R1 = Y, R2 = Z.
MUL R3, R0, R1
MUL R4, R3, R2
ADD R5, R4, R3
MUL R6, R1, R2
ADD R7, R5, R6
Total we need 3 multiplication operations and 2 add operations.
Total cycles needed = 3*2+2 = 8
Assuming R0 = X, R1 = Y, R2 = Z.
MUL R3, R0, R1
MUL R4, R3, R2
ADD R5, R4, R3
MUL R6, R1, R2
ADD R7, R5, R6
Total we need 3 multiplication operations and 2 add operations.
Total cycles needed = 3*2+2 = 8
Question 3 |
Minimum number of NAND gates required to implement the following binary equation
4 | |
5 | |
3 | |
6 |
Question 3 Explanation:
AND-OR (or SOP)realization is easily convertible into NAND-NAND realization.
NOT-OR is equivalent to NAND.
Y = (A’+B’) (C+D)
Y = (A’+B’)C + (A’+B’)D
Let X= (A’+B’) , Y= C, and Z= D
One NAND gate is needed for implementing X= (A’ + B’).
Y= XY + XZ
Y= [(XY)’ (XZ)’]’
Three NAND gates are needed for [(XY)’ (XZ)’]’.
Total Four NAND gates are required to implement thY = (A’+B’) (C+D).
NOT-OR is equivalent to NAND.
Y = (A’+B’) (C+D)
Y = (A’+B’)C + (A’+B’)D
Let X= (A’+B’) , Y= C, and Z= D
One NAND gate is needed for implementing X= (A’ + B’).
Y= XY + XZ
Y= [(XY)’ (XZ)’]’
Three NAND gates are needed for [(XY)’ (XZ)’]’.
Total Four NAND gates are required to implement thY = (A’+B’) (C+D).
Question 4 |
If ABCD is a 4-bit binary number, then what is code generated by the following circuit?
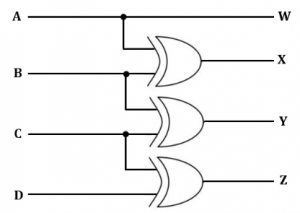
BCD code | |
Gray code | |
8421 code | |
Excess-3 code |
Question 4 Explanation:
In a Gray code, two successive values differ in only one bit.
The given circuit takes ABCD as input and produce WXYZ as its corresponding gray code.
W = A,
X = A ⊕ B,
Y = B ⊕ C,
Z = C ⊕ D.
The given circuit takes ABCD as input and produce WXYZ as its corresponding gray code.
W = A,
X = A ⊕ B,
Y = B ⊕ C,
Z = C ⊕ D.
Question 5 |
The number of tokens in the following C code segment is
switch(inputvalue)
{
case 1;b=c*d; break;
Default : b = b++ ; break;
}
switch(inputvalue)
{
case 1;b=c*d; break;
Default : b = b++ ; break;
}
27 | |
29 | |
26 | |
24 |
Question 5 Explanation:
Switch1(2 inputvalue3 )4
{5
Case6 17 :8 b9 =10 c11 *12 d13 ;14 break15 ;16
Default17 :18 b19 =20 b21 ++22 ;23 break24 ;25
}26
{5
Case6 17 :8 b9 =10 c11 *12 d13 ;14 break15 ;16
Default17 :18 b19 =20 b21 ++22 ;23 break24 ;25
}26
Question 6 |
In a two-pass assembler, resolution of subroutine calls and inclusion of labels in the symbol table is done during
Second pass | |
First pass and second pass respectively | |
Second pass and first pass respectively | |
First pass |
Question 6 Explanation:
In two pass assembler, each pass scans the program, the first pass generates the symbol table and the second pass generates the machine code.
So, inclusion of labels in symbol table is done in first pass and resolution of subroutine is done in second pass.
So, inclusion of labels in symbol table is done in first pass and resolution of subroutine is done in second pass.
Question 7 |
What is the in-order successor of 15 in the given binary search tree?
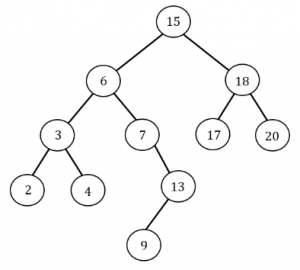
18 | |
6 | |
17 | |
20 |
Question 7 Explanation:
In Binary Tree, Inorder successor of a node is the next node in Inorder traversal of the Binary Tree. Inorder Successor is NULL for the last node in Inorder traversal.
In Binary Search Tree, Inorder Successor of an input node can also be defined as the node with the smallest key greater than the key of input node. So, it is sometimes important to find next node in sorted order.
Hence next node in sorted order for 15 is 17.
In Binary Search Tree, Inorder Successor of an input node can also be defined as the node with the smallest key greater than the key of input node. So, it is sometimes important to find next node in sorted order.
Hence next node in sorted order for 15 is 17.
Question 8 |
The minimum height of an AVL tree with n nodes is
Ceil (log2 (n+1)) | |
1.44 log2n | |
Floor (log2 (n+1)) | |
1.64 log2n |
Question 8 Explanation:
Minimum: ceil(log2(n+1))
Maximum: floor(1.44*log2(n+2)-.328)
Node: Option B is most appropriate among all.
Maximum: floor(1.44*log2(n+2)-.328)
Node: Option B is most appropriate among all.
Question 9 |
The master theorem
Assumes the subproblems are unequal sizes | |
Can be used if the subproblems are of equal size | |
Cannot be used for divide and conquer algorithms | |
Cannot be used for asymptotic complexity analysis |
Question 9 Explanation:
FALSE: The master theorem assumes the subproblems are equal sizes.
TRUE: It can be used if the subproblems are of equal size and unequal size.
FALSE: It can be used for divide and conquer algorithms
FALSE: It can be used for asymptotic complexity analysis
TRUE: It can be used if the subproblems are of equal size and unequal size.
FALSE: It can be used for divide and conquer algorithms
FALSE: It can be used for asymptotic complexity analysis
Question 10 |
Raymond’s tree based algorithm ensures
No starvation, but deadlock may occur in rare clases | |
No deadlock but starvation may occur | |
Neither deadlock nor starvation can occur | |
Deadlock may occur in cases where the process is already starved |
Question 10 Explanation:
This algorithm creates a tree data structure and hence avoids a cycle. Therefore, deadlock is not possible. A site can enter the critical section on receiving the token even when its request is not on the top of the request queue. Hence, starvation is possible.
Question 11 |
Which of the following algorithms defines time quantum?
Shortest job scheduling algorithm | |
Round robin scheduling algorithm | |
Priority scheduling algorithm | |
Multilevel queue scheduling algorithm |
Question 11 Explanation:
Round Robin uses time quantum to fairly allocate CPU for each process in the system.
Question 12 |
Dispatch latency is defined as
The speed of dispatching a process from running to the ready state | |
The time of dispatching a process from running to ready state and keeping the CPU idle | |
The time to stop one process and start running another one | |
None of these |
Question 12 Explanation:
The time it takes for the dispatcher to stop one process and start another is known as the dispatch latency
Question 13 |
An aid to determine the deadlock occurrence is
Resource allocation graph | |
Starvation graph | |
Inversion graph | |
None of the above |
Question 13 Explanation:
Resource allocation graph (RAG) is a diagrammatic representation of processes and the resources in a system. Visually one can determine the occurrence of deadlock using RAG.
Question 14 |
Consider the following page reference string
1 2 3 4 2 1 5 6 2 1 2 3 7 6 3 2 1 2 3 6
What are the minimum number of frames required to get a single page fault for the above sequence assuming LRU replacement strategy?
1 2 3 4 2 1 5 6 2 1 2 3 7 6 3 2 1 2 3 6
What are the minimum number of frames required to get a single page fault for the above sequence assuming LRU replacement strategy?
7 | |
4 | |
6 | |
5 |
Question 14 Explanation:
The minimum number of frames required are 6. If we use 4 frames or 5 frames, we get more than one-page fault using LRU page replacement algorithm.
Question 15 |
Three CPU-bound tasks with execution times of 15, 12 and 5 time units respectively arrive at times , t and 8, respectively. If the operating system implements a shortest remaining time first scheduling algorithm, what should be the value of t to have 4 context switches?
Ignore the context switches at time 0 and at the end.
Ignore the context switches at time 0 and at the end.
0 < t < 3 | |
t = 0 | |
t <= 3 | |
3 < t < 8 |
Question 15 Explanation:
In the question it asked to find the arrival time (t) of process (P2), such that the number of context switches is exactly 4 using SRTF scheduling algorithm. It can be simply verified by taking t=1 and t=2, which causes 4 context switches. So, 0< t < 3. At, t=0 and and t >=3, no of context switches are not exactly 4.
Question 16 |
Context free languages are closed under
Union , intersection | |
Union , kleene closure | |
Intersection, complement | |
Complement, kleene closure |
Question 16 Explanation:
CFL are closed under Union and Kleene closure but not closed under complement,
intersection.
Question 17 |
Which of the following is true?
Every subset of a regular set is regular | |
Every finite subset of non-regular set is regular | |
The union of two non regular set is not regular | |
Infinite union of finite set is regular |
Question 17 Explanation:
Every finite subset of any set is always regular because of finiteness.
Question 18 |
The language which is generated by the grammar S aSa | bSb | a | b over the alphabet {a,b} is the set of
Strings that begin and end with the same symbol | |
All odd and even length palindromes | |
All odd length palindromes | |
All even length palindromes |
Question 18 Explanation:
The grammar generates {a, b, aaa, aba, bab, bbb, aaaaa, aabaa, …}
So the grammar generate odd length palindrome.
So the grammar generate odd length palindrome.
Question 19 |
Which of the following classes of languages can validate an IPv4 address in dotted decimal format? It is to be ensured that the decimal values lie between 0 and 255.
RE and higher | |
CFG and higher | |
CSG and higher | |
Recursively enumerable language |
Question 19 Explanation:
To ensure that decimal value lie between 0 and 255 we can make finite automata as
number of decimal values between 0 and 255 is finite. So RE (regular) and higher is correct.
Question 20 |
Minimum number of states required in DFA accepting binary strings not ending in “101” is
3 | |
4 | |
5 | |
6 |
Question 20 Explanation:
There are 20 questions to complete.