UGC NET CS 2016 Aug- paper-2
Question 1 |
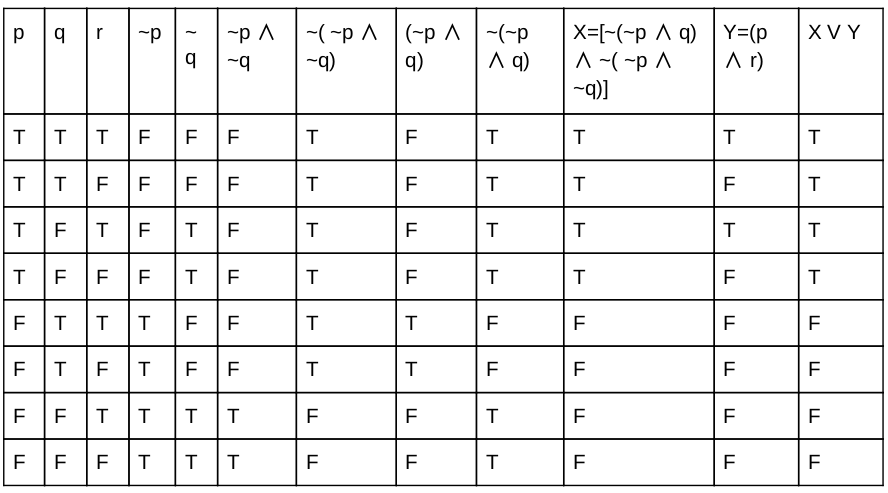
The Boolean function [~(~p ∧ q) ∧ ~( ~p ∧ ~q)] ∨ (p ∧ r) is equal to the Boolean function:
q | |
p ∧ r | |
p ∨ q | |
p |
Question 1 Explanation:
Question 2 |
Let us assume that you construct ordered tree to represent the compound proposition (~ (p ∧ q)) ↔ (~ p ∨ ~ q) Then, the prefix expression and post-fix expression determined using this ordered tree are given as ____ and _____ respectively.
↔~∧pq∨ ~ ~ pq, pq∧~p~q~∨↔ | |
↔~∧pq∨ ~ p~q, pq∧~p~q~∨↔ | |
↔~∧pq∨ ~ ~ pq, pq∧~p~~q∨↔ | |
↔~∧pq∨ ~ p~ q, pq∧~p~ ~q∨↔ |
Question 2 Explanation:
Step-1: Given compound proposition is
(~(p ∧ q))↔(~ p ∨ ~ q)
It is clearly specifying that
↔ is a root
(~(p ∧ q)) is left subtree
(~p ∨ ~q) is right subtree.
Step-2: Finally the tree is looks like
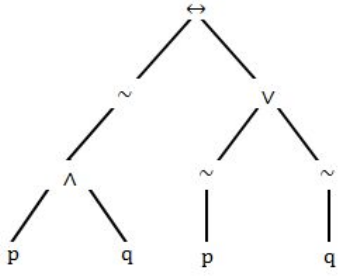
Step-3: Prefix operation traverse through Root,left and Right ↔~∧pq∨ ~ p~q Step-4: Postfix operation traverse through Left,Right and Root.
pq∧~p~q~∨↔
(~(p ∧ q))↔(~ p ∨ ~ q)
It is clearly specifying that
↔ is a root
(~(p ∧ q)) is left subtree
(~p ∨ ~q) is right subtree.
Step-2: Finally the tree is looks like

Step-3: Prefix operation traverse through Root,left and Right ↔~∧pq∨ ~ p~q Step-4: Postfix operation traverse through Left,Right and Root.
pq∧~p~q~∨↔
Question 3 |
Let A and B be sets in a finite universal set U. Given the following:
|A – B|, |A ⊕ B|, |A| + |B| and |A ∪ B|
Which of the following is in order of increasing size ?
|A – B| ≤ |A ⊕ B| ≤ |A| + |B| ≤ |A ∪ B| | |
|A ⊕ B| ≤ |A – B| ≤ |A ∪ B| ≤ |A| + |B| | |
|A ⊕ B| ≤ |A| + |B| ≤ |A – B| ≤ |A ∪ B| | |
|A – B| ≤ |A ⊕ B| ≤ |A ∪ B| ≤ |A| + |B| |
Question 3 Explanation:
Step-1: Let A and B be sets in a finite universal set U.
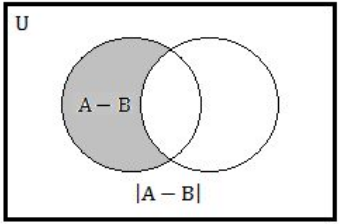
Step-2: |A–B| we can also write into |A|-|A ∩ B| and equivalent Venn diagram is
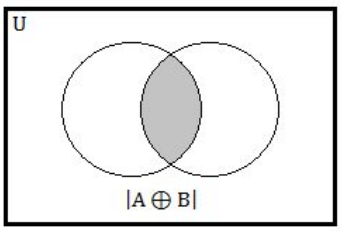
Step-3: |A⊕B| We can also write into |A|+|B|- 2|A∩B| and equivalent Venn diagram is
Step-4: |A| + |B| We can represented into |A| + |B| and equivalent Venn diagram is
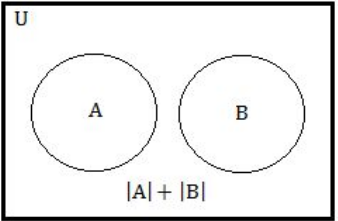
Step-5: |A∪B| We can also write into |A|+|B|- |A∩B| and equivalent Venn diagram is
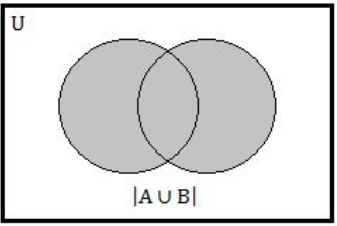
Step-6: |A – B| ≤ |A ⊕ B| ≤ |A ∪ B| ≤ |A| + |B| is correct order.
Step-2: |A–B| we can also write into |A|-|A ∩ B| and equivalent Venn diagram is

Step-3: |A⊕B| We can also write into |A|+|B|- 2|A∩B| and equivalent Venn diagram is

Step-4: |A| + |B| We can represented into |A| + |B| and equivalent Venn diagram is

Step-5: |A∪B| We can also write into |A|+|B|- |A∩B| and equivalent Venn diagram is

Step-6: |A – B| ≤ |A ⊕ B| ≤ |A ∪ B| ≤ |A| + |B| is correct order.
Question 4 |
What is the probability that a randomly selected bit string of length 10 is a palindrome?
1/64 | |
1/32 | |
1/8 | |
1⁄4 |
Question 4 Explanation:
Palindrome is a number that remains the same when its digits are reversed.
Ex: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121...,
Step-1: Here, string length is 10. If we consider first 5 numbers as random choices like 0 or 1.
Remaining 5 numbers are fixed. Total number of possibilities are 2 10 . But we are only considering first 5 choices. The probability is 2 5 .
Step-2: The probability 2 5 /2 10
= 1/2 5
= 1/32
Ex: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121...,
Step-1: Here, string length is 10. If we consider first 5 numbers as random choices like 0 or 1.
Remaining 5 numbers are fixed. Total number of possibilities are 2 10 . But we are only considering first 5 choices. The probability is 2 5 .
Step-2: The probability 2 5 /2 10
= 1/2 5
= 1/32
Question 5 |
Given the following graphs:
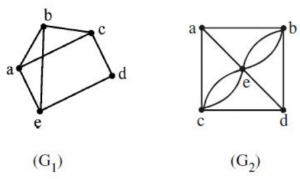
Which of the following is correct?

Which of the following is correct?
G 1 contains Euler circuit and G 2 does not contain Euler circuit. | |
G 1 does not contain Euler circuit and G 2 contains Euler circuit. | |
Both G 1 and G 2 do not contain Euler circuit. | |
Both G 1 and G 2 contain Euler circuit. |
Question 5 Explanation:

Step-1: G1 have odd number of vertices. So, it is not euler circuit.
Step-2: G2 also have odd number of vertices. So, it not euler circuit.
Question 6 |
The octal number 326.4 is equivalent to
(214.2) 10 and (D6.8)) 16 | |
(212.5) 10 and (D6.8)) 16 | |
(214.5) 10 and (D6.8)) 16 | |
(214.5) 10 and (D6.4)) 16 |
Question 6 Explanation:
(326.4) 8 = ( ?)
Step1: First convert given octal no. to binary number because it will be easier to solve this way.
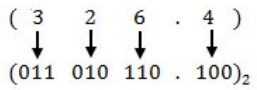
Step 2: Now convert above binary no. into decimal .
(011010110.100) 2
= ( 1 * 2 7 ) + ( 1 × 2 6 ) + ( 1 × 2 4 ) + ( 1 × 2 2 ) + ( 1 × 2 1 ) · [ 1 × ( 1/2) ]
= (214.5) 10
(326.4) 8 = (?) 16 Step 1: Convert given octal no. into binary no.
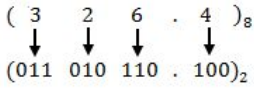
Step 2: Now convert above binary no. into decimal .
(011010110.100) 2
= ( 1 * 2 7 ) + ( 1 × 2 6 ) + ( 1 × 2 4 ) + ( 1 × 2 2 ) + ( 1 × 2 1 ) · [ 1 × ( 1/2) ]
= (214.5) 10
(326.4) 8 = (?) 16
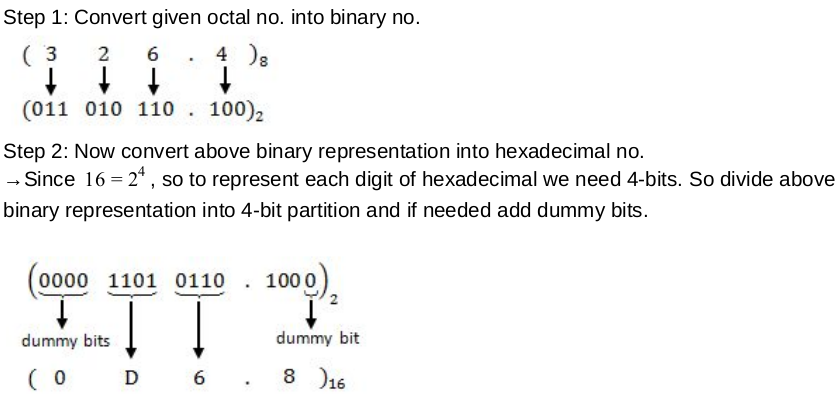
Step1: First convert given octal no. to binary number because it will be easier to solve this way.

Step 2: Now convert above binary no. into decimal .
(011010110.100) 2
= ( 1 * 2 7 ) + ( 1 × 2 6 ) + ( 1 × 2 4 ) + ( 1 × 2 2 ) + ( 1 × 2 1 ) · [ 1 × ( 1/2) ]
= (214.5) 10
(326.4) 8 = (?) 16 Step 1: Convert given octal no. into binary no.

Step 2: Now convert above binary no. into decimal .
(011010110.100) 2
= ( 1 * 2 7 ) + ( 1 × 2 6 ) + ( 1 × 2 4 ) + ( 1 × 2 2 ) + ( 1 × 2 1 ) · [ 1 × ( 1/2) ]
= (214.5) 10
(326.4) 8 = (?) 16

Question 7 |
Which of the following is the most efficient to perform arithmetic operations on the numbers?
Sign-magnitude | |
1’s complement | |
2’s complement | |
9’s complement |
Question 7 Explanation:
2’s complement has single representation for zero , but Sign-magnitude, 1’s complement and 9’s complement have two representations for 0 (i.e., both positive zero and negative zero).
While doing arithmetic operations like addition or subtraction using 1's complement(or 9's complement), we have to add an extra carry bit, i.e 1 to the result to get the correct answer. 2's complement doesn't require such extra calculation.
Question 8 |
The Karnaugh map for a Boolean function is given as
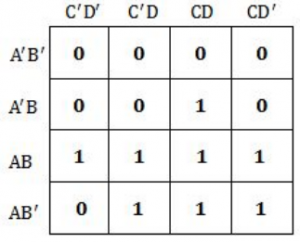
The simplified Boolean equation for the above Karnaugh Map is

The simplified Boolean equation for the above Karnaugh Map is
AB + CD + AB’ + AD | |
AB + AC + AD + BCD | |
AB + AD + BC + ACD | |
AB + AC + BC + BCD |
Question 8 Explanation:
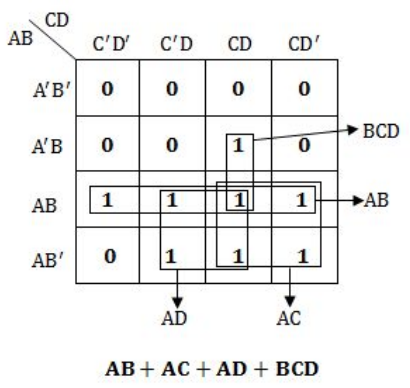
Question 9 |
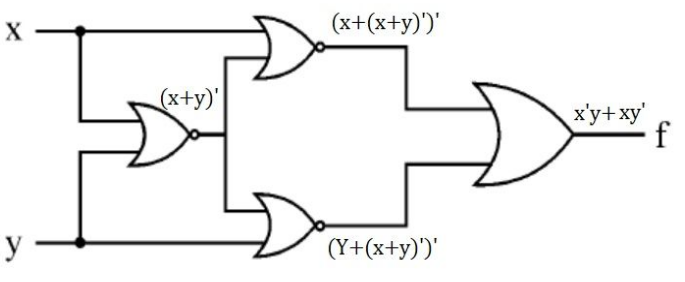
Which of the following logic operations is performed by the following given combinational circuit?


EXCLUSIVE-OR | |
EXCLUSIVE-NOR | |
NAND | |
NOR |
Question 9 Explanation:

Question 10 |
Match the following:


a-iii, b-ii, c-iv, d-i | |
a-ii, b-iv, c-i, d-iii | |
a-ii, b-i, c-iv, d-iii | |
a-iii, b-i, c-iv, d-ii |
Question 10 Explanation:
a. Controlled Inverter : A circuit that transmits a binary word or its1’s complement.
b. Full adder : A circuit that can add 3 bits. It adds two data bits(ai,bi) and also carry bit(ci).
c. Half adder : A logic circuit that adds 2 bits(ai,bi).
d. Binary adder : A circuit that can add two binary numbers(A and B). Collection of Full adders form a binary adder.
b. Full adder : A circuit that can add 3 bits. It adds two data bits(ai,bi) and also carry bit(ci).
c. Half adder : A logic circuit that adds 2 bits(ai,bi).
d. Binary adder : A circuit that can add two binary numbers(A and B). Collection of Full adders form a binary adder.
Question 11 |
Given i= 0, j = 1, k = –1, x = 0.5, y = 0.0 What is the output of given ‘C’ expression ?
x * 3 && 3 || j | k
x * 3 && 3 || j | k
-1 | |
0 | |
1 | |
2 |
Question 11 Explanation:
Step-1: Evaluate x * 3 because multiplication has more priority than remaining operators x * 3→ 1.5
Step-2: && is logical AND. Both the statements are TRUE, then it returns 1 otherwise 0.
1.5 && 3 is TRUE. So, it returns 1.
Step-3: j | k is bitwise OR operator. It returns -1.
Step-4: ((x * 3) && 3) || (j | k) islogical OR operator. It returns 1
Note: The precedence is ((x * 3) && 3) || (j | k)
Step-2: && is logical AND. Both the statements are TRUE, then it returns 1 otherwise 0.
1.5 && 3 is TRUE. So, it returns 1.
Step-3: j | k is bitwise OR operator. It returns -1.
Step-4: ((x * 3) && 3) || (j | k) islogical OR operator. It returns 1
Note: The precedence is ((x * 3) && 3) || (j | k)
Question 12 |
The following ‘C’ statement :
int *f [ ] ( );
declares:
A function returning a pointer to an array of integers. | |
Array of functions returning pointers to integers. | |
A function returning an array of pointers to integers. | |
An illegal statement. |
Question 12 Explanation:
int *f [ ] ( ); It declares array of functions returning pointers to integers.
There are 12 questions to complete.
