GATE 2008
Question 1 |
equals1 | |
-1 | |
∞ | |
-∞ |
Question 1 Explanation:
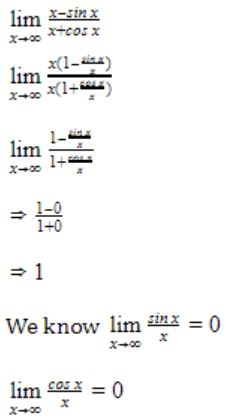
Question 2 |
If P, Q, R are subsets of the universal set U, then (P∩Q∩R) ∪ (Pc∩Q∩R) ∪ Qc ∪ Rc is
Qc ∪ Rc | |
P ∪ Qc ∪ Rc | |
Pc ∪ Qc ∪ Rc | |
U |
Question 2 Explanation:
Given,
(P∩Q∩R)∪(Pc∩Q∩R)∪Qc∪Rc
It can be written as the p.q.r + p'.q.r +q' + r'
=> (p+p').q.r + q' + r'
=> q.r + (q'+r')
=> q.r + q' + r' = 1 i.e., U
(P∩Q∩R)∪(Pc∩Q∩R)∪Qc∪Rc
It can be written as the p.q.r + p'.q.r +q' + r'
=> (p+p').q.r + q' + r'
=> q.r + (q'+r')
=> q.r + q' + r' = 1 i.e., U
Question 3 |
The following system of equations
-
x1 + x2 + 2x3 = 1
x1 + 2x2 + 3x3 = 2
x1 + 4x2 + ax3 = 4
has a unique solution. The only possible value(s) for a is/are
0 | |
either 0 or 1 | |
one of 0, 1 or -1 | |
any real number |
Question 3 Explanation:
The conjugate matrix [A|B] is
When a-5 = 0, then rank(A) = rank[A|B]<3,
So infinite number of solutions.
But, it is given that the given system has unique solution i.e., rank(A) = rank[A|B] = 3 will be retain only if a-5 ≠ 0.
When a-5 = 0, then rank(A) = rank[A|B]<3,
So infinite number of solutions.
But, it is given that the given system has unique solution i.e., rank(A) = rank[A|B] = 3 will be retain only if a-5 ≠ 0.
Question 4 |
In the IEEE floating point representation, the hexadecimal value 0×00000000 corresponds to
the normalized value 2 - 127 | |
the normalized value 2 - 126 | |
the normalized value + 0 | |
the special value + 0 |
Question 4 Explanation:
Value is ±0 if M=0 and E=0.
Question 5 |
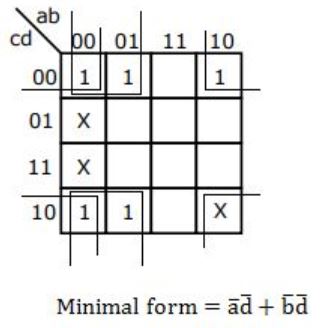
In the Karnaugh map shown below, X denotes a don’t care term. What is the minimal form of the function represented by the Karnaugh map?
 | |
 | |
 | |
 |
Question 5 Explanation:
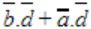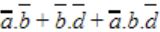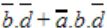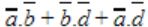Question 6 |
Let r denote number system radix. The only value(s) of r that satisfy the equation 
is/are
decimal 10 | |
decimal 11 | |
decimal 10 and 11 | |
any value > 2 |
Question 6 Explanation:
√121r = 11r
(r2 + 2r + 1)1/2 = r + 1
(r + 1)2 * 1/2 = r + 1
r + 1 = r + 1 Any value of r will satisfy the above equation. But the radix should be greater than 2 because the 121 has 2. So r > 2 is correct.
(r2 + 2r + 1)1/2 = r + 1
(r + 1)2 * 1/2 = r + 1
r + 1 = r + 1 Any value of r will satisfy the above equation. But the radix should be greater than 2 because the 121 has 2. So r > 2 is correct.
Question 7 |
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity
θ(n) | |
θ(m) | |
θ(m+n) | |
θ(mn) |
Question 7 Explanation:
To find the number of connected components using either BFS or DFS time complexity is θ(m+n).
Suppose if we are using Adjacency matrix means it takes θ(n2).
Suppose if we are using Adjacency matrix means it takes θ(n2).
Question 8 |
Given f1, f3 and f in canonical sum of products form (in decimal) for the circuit
- f1 = Σm(4,5,6,7,8)
f3 = Σm(1,6,15)
f = Σm(1,6,8,15)
then f2 is
Σm(4,6) | |
Σm(4,8) | |
Σm(6,8) | |
Σm(4,6,8) |
Question 8 Explanation:
f = f1* f2 + f3
f1*f2 is intersection of minterms of f1 and f2
f = (f1*f2) + f3 is union of minterms of (f1*f2) and f3
Σm(1,6,8,15) = Σm(4,5,6,7,8) * f2 + Σm(1,6,15)
Options A, B and D have minterm m4 which result in Σm(1,4,6,15), Σm(1,4,6,8, 15) and Σm(1,4,6,8, 15)respectively and they are not equal to f.
Option C : If f2 = Σm(6,8)
RHS: Σm(4,5,6,7,8) * Σm(6,8) + Σm(1,6,15)
= Σm(6,8) + Σm(1,6,15)
= Σm(1,6,8,15)
= f = LHS
f1*f2 is intersection of minterms of f1 and f2
f = (f1*f2) + f3 is union of minterms of (f1*f2) and f3
Σm(1,6,8,15) = Σm(4,5,6,7,8) * f2 + Σm(1,6,15)
Options A, B and D have minterm m4 which result in Σm(1,4,6,15), Σm(1,4,6,8, 15) and Σm(1,4,6,8, 15)respectively and they are not equal to f.
Option C : If f2 = Σm(6,8)
RHS: Σm(4,5,6,7,8) * Σm(6,8) + Σm(1,6,15)
= Σm(6,8) + Σm(1,6,15)
= Σm(1,6,8,15)
= f = LHS
Question 9 |
Which of the following is true for the language {ap|p is a prime} ?
It is not accepted by a Turing Machine | |
It is regular but not context-free
| |
It is context-free but not regular | |
It is neither regular nor context-free, but accepted by a Turing machine |
Question 9 Explanation:
Finding prime number cannot be done by FA or PDA, so it cannot be regular or CFL. This language can be recognized by LBA, hence it can be accepted by Turing Machine.
Question 10 |
Which of the following are decidable?
-
I. Whether the intersection of two regular languages is infinite
II. Whether a given context-free language is regular
III. Whether two push-down automata accept the same language
IV. Whether a given grammar is context-free
I and II | |
I and IV | |
II and III | |
II and IV |
Question 10 Explanation:
The intersection of two regular languages is always a regular language (by closure property of regular language) and testing infiniteness of regular language is decidable. Hence statement I is decidable.
Statement IV is also decidable, we need to check that whether the given grammar satisfies the CFG rule (TYPE 2 grammar productions).
But statements II and III are undecidable, as there doesn’t exist any algorithm to check whether a given context-free language is regular and whether two push-down automata accept the same language.
Statement IV is also decidable, we need to check that whether the given grammar satisfies the CFG rule (TYPE 2 grammar productions).
But statements II and III are undecidable, as there doesn’t exist any algorithm to check whether a given context-free language is regular and whether two push-down automata accept the same language.
Question 11 |
Which of the following describes a handle (as applicable to LR-parsing) appropriately?
It is the position in a sentential form where the next shift or reduce operation will occur.
| |
It is non-terminal whose production will be used for reduction in the next step. | |
It is a production that may be used for reduction in a future step along with a position in the sentential form where the next shift or reduce operation will occur.
| |
It is the production p that will be used for reduction in the next step along with a position in the sentential form where the right hand side of the production may be found.
|
Question 11 Explanation:
A handle is the production p that will be used for reduction in the next step along with a position in the sentential form where the right hand side of the production may be found.
Question 12 |
Some code optimizations are carried out on the intermediate code because
They enhance the portability of the compiler to other target processors | |
Program analysis is more accurate on intermediate code than on machine code
| |
The information from dataflow analysis cannot otherwise be used for optimization | |
The information from the front end cannot otherwise be used for optimization |
Question 12 Explanation:
The code-optimization on intermediate code generation will always enhance the portability of the compiler to target processors. The main reason behind this is, as the intermediate code is independent of the target processor on which the code will be executed, so the compiler is able to optimize the intermediate code more conveniently without bothering the underlying architecture of target processor.
Question 13 |
If L and 
are recursively enumerable, then L is
regular | |
context-free | |
context-sensitive | |
recursive |
Question 13 Explanation:
If L is recursive enumerable, then it implies that there exist a Turing Machine (lets say M1) which always HALT for the strings which is in L.
If are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of
Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
If
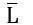are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of
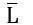Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
Question 14 |
What is the maximum size of data that the application layer can pass on to the TCP layer below?
Any size | |
216 bytes-size of TCP header | |
216 bytes | |
1500 bytes |
Question 14 Explanation:
Application Layer - Any size
Transport Layer - 65515 byte
Network layer - 65535 byte
Data link layer - 1500 byte
Transport Layer - 65515 byte
Network layer - 65535 byte
Data link layer - 1500 byte
Question 15 |
Which of the following tuple relational calculus expression(s) is/are equivalent to ∀t ∈ r(P(t))?
- I. ¬∃t ∈ r(P(t))
II. ∃t ∉ r(P(t))
III. ¬∃t ∈ r(¬P(t))
IV. ∃t ∉ r(¬P(t))
I only | |
II only | |
III only | |
III and IV only |
Question 15 Explanation:
Demorgan law:
∀xP(x) ≡ ∼∃x(∼P(x))
∼∀x(∼P(x)) ≡ ∃x(P(x))
Given: ∀t ∈ r(P(t))------ (1)
As per Demorgan law
(1) ⇒ ∼∃t ∈ r(∼P(t))
which is option (III).
∀xP(x) ≡ ∼∃x(∼P(x))
∼∀x(∼P(x)) ≡ ∃x(P(x))
Given: ∀t ∈ r(P(t))------ (1)
As per Demorgan law
(1) ⇒ ∼∃t ∈ r(∼P(t))
which is option (III).
Question 16 |
A clustering index is defined on the fields which are of type
non-key and ordering | |
non-key and non-ordering | |
key and ordering
| |
key and non-ordering
|
Question 16 Explanation:
Create index files, fields could be non-key attributes and which are in ordered form so as to form clusters easily.
Question 17 |
Which of the following system calls results in the sending of SYN packets?
socket | |
bind | |
listen | |
connect |
Question 17 Explanation:
When connect( ) is called by client, following three way handshake happens to establish the connection in TCP.
1) The client requests a connection by sending a SYN (synchronize) message to the server.
2) The server acknowledges this request by sending SYN-ACK back to the client.
3) The client responds with an ACK, and the connection is established.
1) The client requests a connection by sending a SYN (synchronize) message to the server.
2) The server acknowledges this request by sending SYN-ACK back to the client.
3) The client responds with an ACK, and the connection is established.
Question 18 |
Which combination of the integer variables x, y and z makes the variable a get the value 4 in the following expression?
a = (x > y) ? ((x > z) ? x : z) : ((y > z) ? y : z)
x = 3, y = 4, z = 2 | |
x = 6, y = 5, z = 3 | |
x = 6, y = 3, z = 5 | |
x = 5, y = 4, z = 5 |
Question 18 Explanation:
Required final output value of a=4.
→ We can directly eliminate the options B & C, because none of the variable can assign a value 4.
→ Given explanation is
a = (x>y)?((x>z)?x:z):((y>z)?y:z)
Option A:
x=3; y=4; z=2
a=(3>4)? ⇒ No
Then evaluate second expression ⇒ (4>2)?Yes
⇒a=y
a=4 (True)
Option D:
x=5; y=4; z=5
a=(5>4) ⇒ Yes
Then evaluate first expression ⇒ (5>5)? No
⇒ a=z ⇒ a=5 (Not true)
⇒ Answer is Option A.
→ We can directly eliminate the options B & C, because none of the variable can assign a value 4.
→ Given explanation is
a = (x>y)?((x>z)?x:z):((y>z)?y:z)
Option A:
x=3; y=4; z=2
a=(3>4)? ⇒ No
Then evaluate second expression ⇒ (4>2)?Yes
⇒a=y
a=4 (True)
Option D:
x=5; y=4; z=5
a=(5>4) ⇒ Yes
Then evaluate first expression ⇒ (5>5)? No
⇒ a=z ⇒ a=5 (Not true)
⇒ Answer is Option A.
Question 19 |
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
MNOPQR | |
NQMPOR | |
QMNPRO | |
QMNPOR |
Question 19 Explanation:
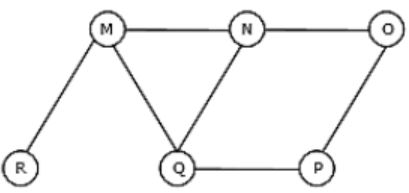
Option C: QMNPRO
→ Queue starts with Q then neighbours of Q is MNP and it is matching with the given string .
→ Now , Next node to be considered is M . Neighbours of M are N, Q and R , but N and Q are already in Queue. So, R is matching with one given string
→ Now, next node to be considered is N. Neighbours of N are M, Q and O, but M and Q are already in Queue. So, O is matching with a given string.
Hence , Option C is Correct.
Similarly, check for option (D).
Question 20 |
The data blocks of a very large file in the Unix file system are allocated using
contiguous allocation | |
linked allocation | |
indexed allocation | |
an extension of indexed allocation |
Question 20 Explanation:
An Unix file system can utilizes an extension of indexed allocation. Because it uses direct blocks, single indirect blocks, double indirect blocks and triple indirect blocks.
Question 21 |
The minimum number of equal length subintervals needed to approximate 
to an accuracy of atleast 
using the trapezoidal rule is
1000e | |
1000 | |
100e | |
100 |
Question 21 Explanation:
Note: Out of syllabus.
There are 21 questions to complete.