APPSC-2016-DL-CS
Question 1 |
The minimum number of edges of a graph containing n vertices and c connected components is
n-c | |
c | |
c(n-1) | |
n/c |
Question 1 Explanation:
We have to find a minimum no. of edges. So for c connected components let's assume c-1 independent vertices which are also c-1 components and remaining 1 component will contain n-(c-1) vertices or n-c+1 vertices. So for minimum no. of edges will be no. of vertices in the single component (which contains n-c+1 vertices) -1, which is
(n-c+1)-1 = n-c
Question 2 |
In first order predicate logic, ∼∀x P(x) is equivalent to Options:
∼∃x P(x) | |
∃x ∼P(x) | |
∀x ∼P(x) | |
the given expression is not a well formed |
Question 2 Explanation:
∼∀x P(x) = ∃x ∼P(x)
Question 3 |
How many different 6-member committees can be formed from 6 men and 4 women with a restriction that each committee should include an equal number of men and women
120 | |
80 | |
420 | |
6045 |
Question 3 Explanation:
Given data,
Committee members=6,
Mens=6
Women=4
Equal numbers of men and women are= ?
3 men out of 6, 3 women out of 4
⇒ 6C3 * 4C3 ways
⇒ 20 * 4
⇒ 80
Note: There are 3 possibilities to consider an equal number of men and women.
Choose 4 men and 4 women then we get 6C4 * 4C4 ways = 15
Choose 2 men and 2 women then we get 6C2 * 4C2 ways = 90
Choose 3 men and 3 women then we get 6C3 * 4C3 ways = 80
Committee members=6,
Mens=6
Women=4
Equal numbers of men and women are= ?
3 men out of 6, 3 women out of 4
⇒ 6C3 * 4C3 ways
⇒ 20 * 4
⇒ 80
Note: There are 3 possibilities to consider an equal number of men and women.
Choose 4 men and 4 women then we get 6C4 * 4C4 ways = 15
Choose 2 men and 2 women then we get 6C2 * 4C2 ways = 90
Choose 3 men and 3 women then we get 6C3 * 4C3 ways = 80
Question 4 |
Consider 4-character long codes generated by using an alphabet consisting of 8-characters with no restriction on the number of repetitions of a character in a code. How many codes at least one character repeated?
2416 | |
6720 | |
1680 | |
4096 |
Question 5 |
How many distinct Boolean functions can be formed from ‘n’ Boolean variables?
n2 | |
2n2 | |
2n | |
2 to the power of 2n |
Question 5 Explanation:
Each “boolean” variable has two possible values i.e 0 and 1.
Number of variables= n
Number of input combinations is 2n.
Each “boolean” function has two possible outputs i.e 0 and 1.
Number of boolean functions possible is 22^n.
Formula: The number of m-ary functions possible with n k-ary variables is mk^n.
Number of variables= n
Number of input combinations is 2n.
Each “boolean” function has two possible outputs i.e 0 and 1.
Number of boolean functions possible is 22^n.
Formula: The number of m-ary functions possible with n k-ary variables is mk^n.
Question 6 |
In order for a function to be invertible, it should be _______
one-one | |
onto | |
both one-one and onto | |
into |
Question 6 Explanation:
A function is invertible if and only if it is both one-one and onto.
Question 7 |
What is the maximum value of the function f(x)=x2-3x+5 in the internal [0,5]?
15 | |
5 | |
3 | |
9 |
Question 7 Explanation:

Question 8 |
In an IT company, given that the probability of finding an employee with programming skills is 0.7, documentation skills is 0.6, and if the probability of finding an employee with either of the skills is 0.9, then what is the probability of finding an employee with both the skills?
0.42 | |
0.5 | |
0.4 | |
0.8 |
Question 8 Explanation:
Let A = probability of finding an employee with programming skills
Let B = probability of finding an employee with documentation skill
So A=0.7
B=0.6
AUB=0.9
Hence ,A∩B = A + B - (AUB)
= 0.7+0.6-0.9
= 0.4
Let B = probability of finding an employee with documentation skill
So A=0.7
B=0.6
AUB=0.9
Hence ,A∩B = A + B - (AUB)
= 0.7+0.6-0.9
= 0.4
Question 9 |
Let A, B and C are finite sets. Which of the following options is TRUE, if X=((A∩B)-(B∩C)) and Y=(A-(A∩C))-(A-B)?
X⊂Y | |
X⊃Y | |
X=Y | |
X-Y≠φ and Y-X≠φ |
Question 9 Explanation:
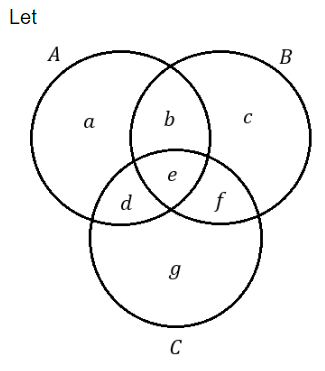
Now,
x=((AB)-(BC))
=(b,c)-(e,f))
=b
y=(A-(AC))-(A-B)
=((a,b,d,e)-(d,e))-(a,d)
=(a,b)-(a,d)
=b
Hence, x=y
Question 10 |
Which of the following options is TRUE with regard to a relation R defined on ordered pairs of integers as given below: (x,y) R (low,up) if x>low and y<up?
R is totally ordered | |
R is partially ordered but not totally ordered
| |
R is an equivalence relation | |
R is neither partially ordered nor an equivalence relation |
Question 10 Explanation:
If a relation is equivalence then it must be
i) Symmetric
ii) Reflexive
iii) Transitive
If a relation is a partial order relation then it must be
i) Reflexive
ii) Anti-symmetric
iii) Transitive
If a relation is total order relation then it must be
i) Reflexive
ii) Symmetric
iii) Transitive
iv) Comparability
Given ordered pairs are (x,y)R(low,up) if (x,up).
Here < , > are using while using these symbols between (x,y) and (y,up) then they are not satisfy the reflexive relation. If they use (x< =low) and (y >=low) then reflexive relation can satisfies.
So, given relation cannot be an Equivalence. Total order relation or partial order relation.
i) Symmetric
ii) Reflexive
iii) Transitive
If a relation is a partial order relation then it must be
i) Reflexive
ii) Anti-symmetric
iii) Transitive
If a relation is total order relation then it must be
i) Reflexive
ii) Symmetric
iii) Transitive
iv) Comparability
Given ordered pairs are (x,y)R(low,up) if (x,up).
Here < , > are using while using these symbols between (x,y) and (y,up) then they are not satisfy the reflexive relation. If they use (x< =low) and (y >=low) then reflexive relation can satisfies.
So, given relation cannot be an Equivalence. Total order relation or partial order relation.
Question 11 |
The Hasse diagram representing a lattice, P when turned upside-down represents the poset, Q. Poset Q is a ______
dual of P | |
Greatest Upper Bound of P | |
Lattice | |
dual of P and Lattice |
Question 11 Explanation:
The Hasse diagram representing a lattice, P when turned upside-down represents the poset Q which is dual of P and lattice.
Question 12 |
A pair of dice is tossed twice. What is the probability of scoring 9 at least in one of the two times?
16/81 | |
17/81 | |
1/36 | |
64/81 |
Question 12 Explanation:
We will use binomial distribution here.
Total possible outcomes will be 6*6=36
Lets first calculate probability of getting sum as 9. We will get sum as 9 when first dice and second dice will have number (3,6) ,(4,5) ,(5,4) ,(6,3). So total 4 possibility are there out of 36.
So Let probability of getting sum as 9 = P(A) = 4/36 = 1/9
Now
Probability of scoring 9 at least in one of the two times
= Probability of scoring 9 exactly one time + Probability of scoring 9 exactly two times

Total possible outcomes will be 6*6=36
Lets first calculate probability of getting sum as 9. We will get sum as 9 when first dice and second dice will have number (3,6) ,(4,5) ,(5,4) ,(6,3). So total 4 possibility are there out of 36.
So Let probability of getting sum as 9 = P(A) = 4/36 = 1/9
Now
Probability of scoring 9 at least in one of the two times
= Probability of scoring 9 exactly one time + Probability of scoring 9 exactly two times

Question 13 |
Which of the following probability distributions is applicable to consider the problem of estimating the probability of exactly two defective items manufactured in an industry in a batch of 20 items, if the probability of manufacture defect is 0.1?
Poisson distribution | |
Binomial distribution | |
Uniform distribution | |
Gaussian distribution |
Question 13 Explanation:
Binomial distribution will be used.
And will be calculated as
20C2 = (0.1)2 (0.9)18
Question 14 |
The propositional expression [(∼P∨Q)→(Q→P)] is
a tautology | |
not a tautology | |
contradiction | |
not a well-formed formula |
Question 14 Explanation:
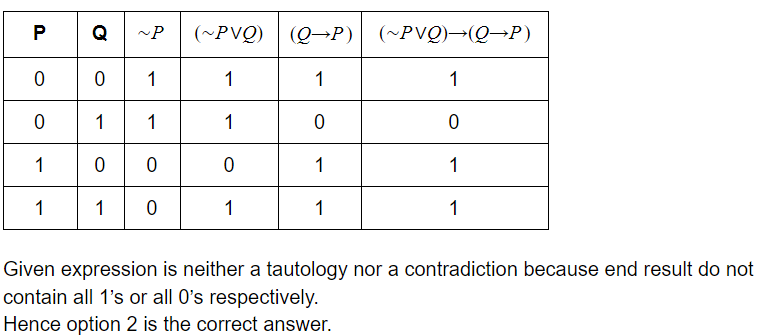
Question 15 |
The maximum number of non-zero elements of a n×n matrix whose [i,j]th element is equal to 0 for all i<j is
n(n-1)/2 | |
n(n+1)/2 | |
n2 | |
n |
Question 15 Explanation:
From given description we can conclude that all the elements above the diagonal are 0. So we can say that,
1st row will have 1 non-zero element,
2nd row will have 2 non zero elements,
3rd row will have 3 non-zero elements ,
:
:
:
nth row will contain n non-zero elements.
Therefore total no. of non-zero elements are,
1+2+3+...........+n = n(n+1)/2
1st row will have 1 non-zero element,
2nd row will have 2 non zero elements,
3rd row will have 3 non-zero elements ,
:
:
:
nth row will contain n non-zero elements.
Therefore total no. of non-zero elements are,
1+2+3+...........+n = n(n+1)/2
Question 16 |
At a given moment a queue contains stored in it. If the capacity of the queue is 6 then which of the following sequence of operations results in a modified queue contents?
delete a, b; and insert e,a,f; | |
insert e,a,f and delete a,b | |
insert e, delete b and insert f
| |
insert e,f, move a to place it between e and f, then delete b
|
Question 17 |
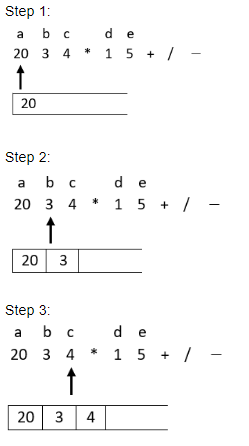
The value of the postfix expression abc*de+/- where a=20, b=3, c=4, d=1 and e=5 is
134 | |
-22 | |
48 | |
18 |
Question 17 Explanation:
Here we will start traversing the expression from left to right and if an operand is encountered then it will be pushed on the top of stack and if an operator is encountered then top two elements will be popped off from the top of stack and current operator is applied on those two operands and then in the end the result of operation will be pushed back on the top of stack. This procedure continues till the whole expression is traversed.


Step: 7
Hence option 4 is the correct answer.

Step: 7
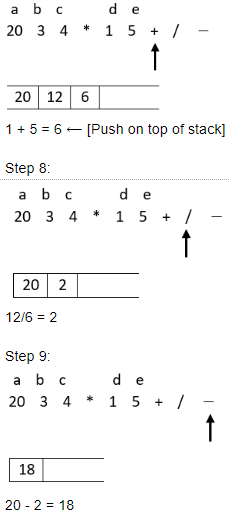
Hence option 4 is the correct answer.
Question 18 |
Consider optimal implementation of two stacks growing in opposite directions in a single array A[n]. If t1 and t2 denote the stack pointers, which of the following, checks for stack full condition?
t2=(n-1) or t1=(n-1) | |
t1=n/2 or t2=(n-1) | |
t1=0 and t2=(n-1) | |
t2=t1+1 |
Question 18 Explanation:
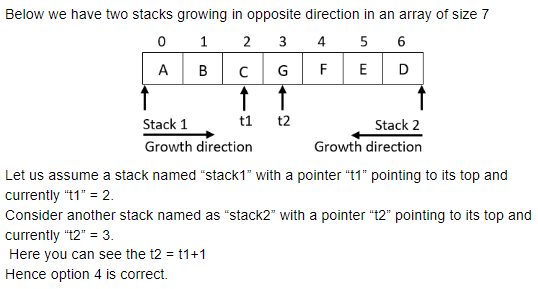
Question 19 |
Which of the following types of the linked list is fastest to delete a node pointed by ‘p’ from a large collection of nodes constituting the list?
doubly linked list | |
singly linked list | |
singly linked circular list | |
singly linked list with header node |
Question 19 Explanation:
Worst case of deleting a node from a linked list is when we are on the last node of the list and we want to delete (n-1)th node from the list. In this case above lists will have the following time complexity:
Doubly linked list: Since it is doubly linked list so last node will have pointer to its previous node(i.e “n-1” ) node. So (n-1)th node can be deleted in O(1) time. Single Linked List: Since in this no node have a pointer to its previous node so even if we have a pointer on last node of the list we have to traverse (n-1) nodes of the given linked list in order to delete (n-1)th node. Hence its time complexity will be O(n). singly linked circular list: For above scenario since the list is unidirect so we have to traverse (n-1) elements in best case in order to delete (n-1)th node even after having a pointer to nth node.
singly linked list with header node is nothing but Single linked list only. So its time complexity will also be O(n).
Hence Doubly linked list is giving best time complexity to delete a node pointed by ‘p’ from a large collection of nodes constituting the list.
Doubly linked list: Since it is doubly linked list so last node will have pointer to its previous node(i.e “n-1” ) node. So (n-1)th node can be deleted in O(1) time. Single Linked List: Since in this no node have a pointer to its previous node so even if we have a pointer on last node of the list we have to traverse (n-1) nodes of the given linked list in order to delete (n-1)th node. Hence its time complexity will be O(n). singly linked circular list: For above scenario since the list is unidirect so we have to traverse (n-1) elements in best case in order to delete (n-1)th node even after having a pointer to nth node.
singly linked list with header node is nothing but Single linked list only. So its time complexity will also be O(n).
Hence Doubly linked list is giving best time complexity to delete a node pointed by ‘p’ from a large collection of nodes constituting the list.
Question 20 |
Singly linked circular list with header pointing to the last node is the data structure preferred in the context of
insertion of a node at a position ‘p’ | |
deletion of a node pointed by ‘p’ | |
reversing the order of the nodes in the list
| |
concatenating two lists into one list |
Question 20 Explanation:
Singly linked circular list with header pointing to the last node is the data structure preferred in the context of concatenating two lists into one list, because it can be done in O(1) time.
Question 21 |
If the inorder and preorder sequence of nodes of a binary tree are CABDFEHG and DCBAGEFH respectively, then the post order sequence is
ABCDEFGH | |
HFEGABCD | |
ABCFHEGD | |
AFHBECGD |
Question 21 Explanation:
Inorder: CABDFEHG
Preorder: DCBAGEFH

Hence, Post-order of above tree will be: ABCFHEGD. Hence, Post-order of above tree will be: ABCFHEGD.
Preorder: DCBAGEFH
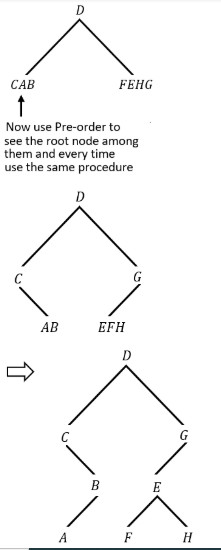
Hence, Post-order of above tree will be: ABCFHEGD. Hence, Post-order of above tree will be: ABCFHEGD.
Question 22 |
Construct a Max-heap dynamically to accomodate a stream of eight integers, 48,34,68,32,19,25,61,53 as a descending priority queue. The leaf node that is farthest from the root is ______
19 | |
68 | |
48 | |
32 |
Question 22 Explanation:
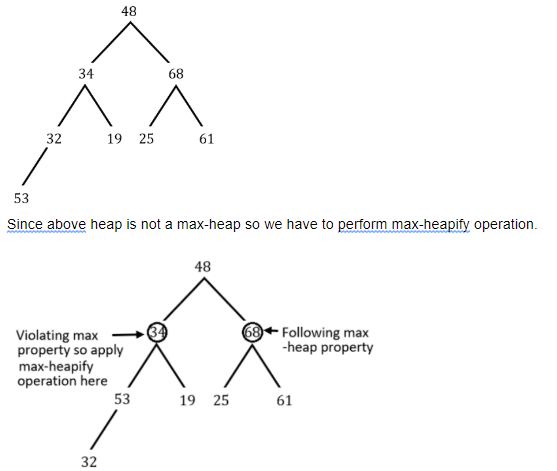

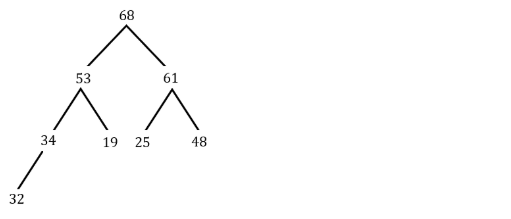
Question 23 |
Which of the following algorithms is fastest to find shortest path from a source node to a destination node in an un-weighted connected graph?
Warshall’s algorithm | |
Floyd’s algorithm | |
Breadth First Traversal | |
Depth First Traversal |
Question 23 Explanation:
warshall algorithm will take O(n^3) time.
Floyd’s algorithm will take O(n^3) time.
Breadth First traversal will take O(m+n) time.
Depth first traversal will work only if the graph is tree.
Hence among the given options Breadth first traversal is best.
Floyd’s algorithm will take O(n^3) time.
Breadth First traversal will take O(m+n) time.
Depth first traversal will work only if the graph is tree.
Hence among the given options Breadth first traversal is best.
Question 24 |
Which of the following algorithms doesn’t require Priority queue for its implementation?
Kruskal’s algorithm | |
Prim’s algorithm | |
Huffman code generation algorithm
| |
Warshall’s algorithm |
Question 24 Explanation:
Kruskal’s ,prims , and huffman code generation algorithm require priority queue. But in floyd warshall we use matrix .
Question 25 |
Consider a large disk file containing records each of considerable size and an identification key. Which of the following methods is suitable to organize the file for faster access to a record given its key?
Apply Keysorting and maintain an index to the randomly ordered disk file | |
Sort the records of the disk file using Merge sort | |
Sort the records of the disk file using Quick sort | |
Apply keysorting and accordingly sort the records of the disk file |
Question 25 Explanation:
Using Primary key indexing all records can be accessed faster.Primary key indexing is based on a key attribute where all the elements of key attribute are arranged in sorted manner.
Question 26 |
Which of the following is preferred to organize very large indexed sequential access disk files for both interactive random access and co-sequential batch processing of its records?
Hashing | |
B-Trees | |
Simple Index | |
B+ Trees |
Question 26 Explanation:
B-tree and B+ Tree are suitable to organize very large indexed sequential access disk files for interactive random access but since in B+ tree each leaf node have a pointer to its next leaf node then it makes the access of co-sequential batch processing of its records easier.
Question 27 |
Which of the following probability distribution functions is used to predict the number of collisions in terms of packing density of a Hash table?
Gaussian distribution | |
Poisson distribution | |
Uniform distribution | |
Binomial distribution |
Question 28 |
The best case time complexity of insertion sort algorithms is ______
O(n) | |
O(1) | |
O(n2) | |
O(n log n) |
Question 28 Explanation:
The best case of insertion sort is when all the elements given in array are already sorted. In that case when insertion sort is applied only one comparison is made for each element of the array. Hence if we have n-elements the n-comparisons will be made. Hence the time complexity will be O(n)
Question 29 |
Which of the following is NOT used for time complexity estimation of an algorithm?
L Hospital Rule
| |
Method of Backward Substitution | |
Master’s theorem | |
Composite Trapezoidal Rule |
Question 29 Explanation:
L hospitals Rule, method of back ward substitution and masters theorem is used for time complexity estimation of an algorithm . But Composite trapezoidal rule gives us a technique to approximate the integral on a given interval [a, b] and not used for time complexity estimation of an algorithm.
Question 30 |
Which type of algorithm design strategy is used in Quick-hull algorithm to find the smallest convex polygon that contains ‘n’ given points in a plane?
Greedy Approach | |
Divide and Conquer approach | |
Dynamic programming | |
Transform and Conquer approach |
Question 30 Explanation:
The QuickHull algorithm is a Divide and Conquer algorithm similar to QuickSort.
Question 31 |
Applying Gaussian Elimination method for solving linear equations isDynamic programming an example of ______
Dynamic programming | |
Greedy approach | |
Transform and Conquer approach | |
Divide and Conquer approach |
Question 31 Explanation:
Gaussian elimination method is transform and conquer approach.This algorithm solves a system of linear equations by first transforming it to another system with a special property that makes finding a solution quite easy.
Question 32 |
Time complexity of an algorithm whose recurrence equation is T(n)=4T(n/2)+n2 and T(1)=1 is expressed as ______
O(n2) | |
O(n2 log n) | |
O(n3) | |
O(n log n) |
Question 32 Explanation:
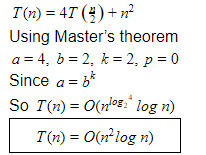
Question 33 |
Twice-around the spanning tree algorithm for solving the Travelling Salesman Problem with Euclidean distances is a ______
2-approximation algorithm | |
1.5 approximation algorithm
| |
1.25 approximation algorithm | |
2.5 approximation algorithm |
Question 34 |
Which of the following problems belong to the class of NP-Complete problems?
Knapsack Problem | |
Hamiltonian Circuit problem | |
Eulerian Circuit Problem | |
Graph Coloring problem |
Question 34 Explanation:
NP Problem: Each input to the problem should be associated with a set of solutions of polynomial length, whose validity can be tested in polynomial time. The complexity class of problems of this form is called NP, an abbreviation for "nondeterministic polynomial time".
NP-Hard: A problem is said to be NP-hard if everything in NP can be transformed in polynomial time into it.
A problem is NP-complete if it is both in NP and NP-hard. The NP-complete problems represent the hardest problems in NP.
The list below contains some well-known problems that are NP-complete when expressed as decision problems.
Boolean satisfiability problem (SAT)
Knapsack problem
Hamiltonian path problem
Travelling salesman problem (decision version)
Subgraph isomorphism problem
Subset sum problem
Clique problem
Vertex cover problem
Independent set problem
Dominating set problem
Graph coloring problem
NP-Hard: A problem is said to be NP-hard if everything in NP can be transformed in polynomial time into it.
A problem is NP-complete if it is both in NP and NP-hard. The NP-complete problems represent the hardest problems in NP.
The list below contains some well-known problems that are NP-complete when expressed as decision problems.
Boolean satisfiability problem (SAT)
Knapsack problem
Hamiltonian path problem
Travelling salesman problem (decision version)
Subgraph isomorphism problem
Subset sum problem
Clique problem
Vertex cover problem
Independent set problem
Dominating set problem
Graph coloring problem
Question 35 |
Which of the following sorting algorithms does in-place sorting with minimal space overhead?
Merge sort | |
Radix sort | |
Heap sort | |
Address Calculation Sort |
Question 35 Explanation:
In-Place sorting algorithm is one which requires only O(1) space in order to sort n-elements.
Merge sort has space complexity of O(n). Hence it is not an in-place sorting algorithm.
Merge sort has space complexity of O(n). Hence it is not an in-place sorting algorithm.
Question 36 |
The principle of replacing a function irrespective of the context is called ______
Static binding | |
referential transparency | |
orthogonality | |
locality of reference |
Question 37 |
Which of the following predicate expressions represent the statement “None of the Students have failed in the test”?
∼∃x(Student(x)∧∼Failed(x)) | |
∼∀x(∼Student(x)∧∼Failed(x)) | |
∀x(∼Student(x)∧FAiled(x)) | |
∼∃x(Student(x)∧Failed(x)) |
There are 37 questions to complete.
