GATE 1994
Question 1 |
FORTRAN implementation do not permit recursion because
they use static allocation for variables | |
they use dynamic allocation for variables | |
stacks are not available on all machines | |
it is not possible to implement recursion on all machines |
→ Recursion requires dynamic allocation of data.
Question 2 |
Let A and B be real symmetric matrices of size n × n. Then which one of the following is true?
AA′ = 1 | |
A = A-1 | |
AB = BA | |
(AB)' = BA |

Question 3 |
Backward Euler method for solving the differential equation dy/dx = f(x,y) is specified by, (choose one of the following).
yn+1 = yn + hf(xn, yn) | |
yn+1 = yn + hf(xn+1, yn+1) | |
yn+1 = yn-1 + 2hf(xn, yn) | |
yn+1 = (1 + h) f(xn+1, yn+1) |
With initial value y(x0) = y0. Here the function f and the initial data x0 and y0 are known. The function y depends on the real variable x and is unknown. A numerical method produces a sequence y0, y1, y2, ....... such that yn approximates y(x0 + nh) where h is called the step size.
→ The backward Euler method is helpful to compute the approximations i.e.,
yn+1 = yn + hf(x n+1, yn+1)
Question 4 |
Let A and B be any two arbitrary events, then, which one of the following is true?
P(A∩B) = P(A)P(B) | |
P(A∪B) = P(A) + P(B) | |
P(A|B) = P(A∩B)P(B) | |
P(A∪B) ≤ P(A) + P(B) |
(B) Happens when A and B are mutually exclusive.
(C) Not happens.
(D) P(A∪B) ≤ P(A) + P(B) is true because P(A∪B) = P(A) + P(B) - P(A∩B).
Question 5 |
An unrestricted use of the “goto” statement is harmful because
it makes it more difficult to verify programs | |
it increases the running time of the programs | |
it increases the memory required for the programs
| |
it results in the compiler generating longer machine code |
Question 6 |
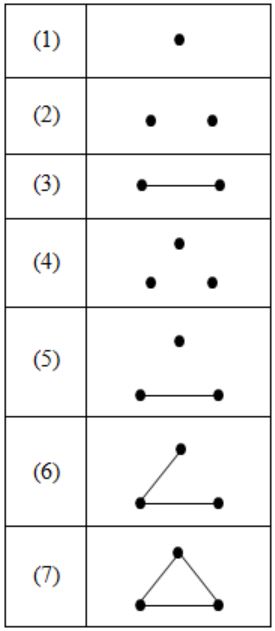
The number of distinct simple graphs with upto three nodes is
15 | |
10 | |
7 | |
9 |
Question 7 |
The recurrence relation that arises in relation with the complexity of binary search is:
T(n) = T(n/2) + k, k a constant | |
T(n) = 2T(n/2) + k, k a constant | |
T(n) = T(n/2) + log n | |
T(n) = T(n/2) + n |
∴ T(n) = 2T(n/2) + k, k a constant
Question 8 |
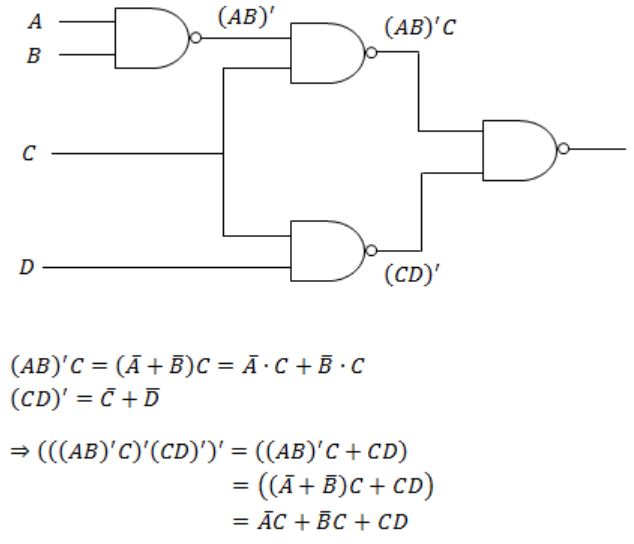
The logic expression for the output of the circuit shown in figure below is:

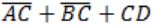 | |
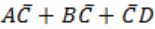 | |
 | |
 | |
None of the above. |
Question 9 |
The tank of matrix is:
0 | |
1 | |
2 | |
3 |

Question 10 |
Some group (G,o) is known to be abelian. Then, which one of the following is true for G?
g = g-1 for every g ∈ G | |
g = g2 for every g ∈ G | |
(goh)2 = g2oh2 for every g,h ∈ G | |
G is of finite order |
For Abelian group, commutative also holds
i.e., (aob) = (boa)
Consider option (C):
(goh)2 = (goh)o(gog)
= (hog)o(goh)
= (ho(gog)oh)
= ((hog2)oh)
= (g2oh)oh
= g2o(hoh)
= g2oh2 [True]
Question 11 |
In a compact single dimensional array representation for lower triangular matrices (i.e all the elements above the diagonal are zero) of size n × n, non-zero elements (i.e elements of the lower triangle) of each row are stored one after another, starting from the first row, the index of the (i, j)th element of the lower triangular matrix in this new representation is:
i + j | |
i + j - 1 | |
j + i(i-1)/2 | |
i + j(j-1)/2 |
If we assume array index starting from 1 then, ith row contains i number of non-zero elements. Before ith row there are (i-1) rows, (1 to i-1) and in total these rows has 1+2+3......+(i-1) = i(i-1)/2 elements.
Now at ith row, the jth element will be at j position.
So the index of (i, j)th element of lower triangular matrix in this new representation is
j = i(i-1)/2
Question 12 |
Generation of intermediate code based on an abstract machine model is useful in compilers because
it makes implementation of lexical analysis and syntax analysis easier | |
syntax-directed translations can be written for intermediate code generation | |
it enhances the portability of the front end of the compiler | |
it is not possible to generate code for real machines directly from high level language programs |
Question 13 |
A memory page containing a heavily used variable that was initialized very early and is in constant use is removed when
LRU page replacement algorithm is used | |
FIFO page replacement algorithm is used | |
LFU page replacement algorithm is used | |
None of the above |
In LRU which can eliminate (or) removed which is least recently used.
In LFU the frequency of the page is more. So it is in constant use so cannot be replaced.
Question 14 |
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1, 2, 3, 4, 5 in that order?
3, 4, 5, 1, 2 | |
3, 4, 5, 2, 1 | |
1, 5, 2, 3, 4 | |
5, 4, 3, 1, 2 |
→ Remaining options are not possible.
Question 15 |
The number of substrings (of all lengths inclusive) that can be formed from a character string of length n is
n | |
n2 | |
n(n-1)/2 | |
n(n+1)/2 |
n = 1
(n-1) = 2
(n-2) = 3
So, Total = n(n+1)/2
Question 16 |
Which of the following conversions is not possible (algorithmically)?
Regular grammar to context free grammar | |
Non-deterministic FSA to deterministic FSA | |
Non-deterministic PDA to deterministic PDA | |
Non-deterministic Turing machine to deterministic Turing machine |
Question 17 |
Linked lists are not suitable data structures of which one of the following problems?
Insertion sort | |
Binary search | |
Radix sort | |
Polynomial manipulation
|
Question 18 |
Which of the following features cannot be captured by context-free grammars?
Syntax of if-then-else statements | |
Syntax of recursive procedures | |
Whether a variable has been declared before its use | |
Variable names of arbitrary length |
Syntactic rules not checking the meaningful things such as if a variable is declared before it use (or) not.
Like this, things are handled by semantic analysis phase.
