GATE 1999
Question 1 |
There is a sample point at which X has the value 5. | |
There is a sample point at which X has value greater than 5. | |
There is a sample point at which X has a value greater than or equal to 5. | |
None of the above |
E(X) = x1P1 + x2P2 + ... + xnPn
In question, E(X) is given as 5.
E(X) = 5, 0≤Pi≤1
P1 + P2 + ... + Pn = 1 [Probability]
Therefore, E(X) = 5 is possible only if atleast one of the xi value is greater than 5.
Question 2 |
n2 | |
2n | |
2n (2) | |
None of the above |
n×n = n2
Now, no. of binary relations possible is
2n2
Because each pair have two possibilities either chosen or not chosen.
Question 3 |
The number of binary strings of n zeroes and k ones that no two ones are adjacent is
n-1Ck | |
nCk | |
nCk+1 | |
None of the above |
XOXOXOXOXOXOX
n+1 gaps can be possible, where 1's can be placed so that no two one's are adjacent. So, no. of ways in which k 1's can be placed in n+1 gaps are,
n+1Ck
Question 4 |
Consider the regular expression (0 + 1) (0 + 1)…. N times. The minimum state finite automation that recognizes the language represented by this regular expression contains
n states | |
n + 1 states | |
n + 2 states | |
None of the above |
DFA:

So, DFA requires (n+2) state.
NFA:

So, NFA requires (n+1) state.
So, final answer will be,
min(n+1, n+2)
= n+1
Question 5 |
Context-free languages are closed under:
Union, intersection | |
Union, Kleene closure | |
Intersection, complement | |
Complement, Kleene closure |
By checking the options only option B is correct.
Question 6 |
Let LD be the set of all languages accepted by a PDA by final state and LE the set of all languages accepted by empty stack. Which of the following is true?
LD = LE | |
LD ⊃ LE | |
LE = LD | |
None of the above |
Question 7 |
 ?
?x NAND X | |
x NOR x | |
x NAND 1 | |
x NOR 1 |

Question 8 |
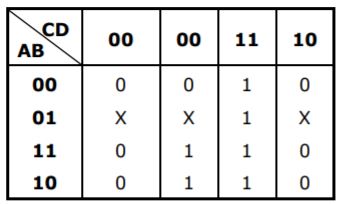
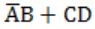 | |
 | |
 | |
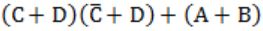 |

⇒ CD+AD = D(A+C)
Question 9 |
Listed below are some operating system abstractions (in the left column) and the hardware components or mechanism (in the right column) that they are abstractions of. Which of the following matching of pairs is correct?
A. Thread 1. Interrupt
B. Virtual address space 2. Memory
C. File system 3. CPU
D. Signal 4. Disk (A) – 2 (B) – 4 (C) – 3 (D) - 1 | |
(A) – 1 (B) – 2 (C) – 3 (D) – 4 | |
(A) – 3 (B) – 2 (C) – 4 (D) - 1 | |
(A) – 4 (B) – 1 (C) – 2 (D) – 3 |

⇒ Threads are handled by CPU.
⇒ Virtual address is a memory type.
⇒ File system is used to manage the disk.
⇒ Interrupt is a signal.
Question 10 |
Which of the following disk scheduling strategies is likely to give the best through put?
Farthest cylinder next | |
Nearest cylinder next | |
First come first served | |
Elevator algorithm |
Nearest cylinder next - SSTF
First come first served - FCFS
Elevator - SCAN
SSTF always serves the request of nearest cylinder first. Due to which the necessary movement gets reduced.
Question 11 |
System calls are usually invoked by using
a software interrupt | |
polling | |
an indirect jump | |
a privileged instruction |
Question 12 |
A sorting technique is called stable if
it takes O (nlog n) time | |
it maintains the relative order of occurrence of non-distinct elements | |
it uses divide and conquer paradigm | |
it takes O(n) space |
Question 13 |
Suppose we want to arrange the n numbers stored in any array such that all negative values occur before all positive ones. Minimum number of exchanges required in the worst case is
n - 1 | |
n | |
n + 1 | |
None of the above |
Now we will swap 1st no. with nth no. and then 2nd no. with (n-1)th no. and then 3rd no. with (n-2)th and so on. Like this we will have to do n/2 swaps in worst case.
Question 14 |
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
then the order of these elements after second pass of the algorithm is:
8, 9, 15, 20, 47, 4, 12, 17, 30, 40 | |
8, 15, 20, 47, 4, 9, 30, 40, 12, 17 | |
15, 20, 47, 4, 8, 9, 12, 30, 40, 17 | |
4, 8, 9, 15, 20, 47, 12, 17, 30, 40 |

Question 15 |
The number of articulation points of the following graph is

0 | |
1 | |
2 | |
3 |
Total no. of articulation points = 3
Question 16 |
If n is a power of 2, then the minimum number of multiplications needed to compute a* is
log2 n | |
√n | |
n-1 | |
n |
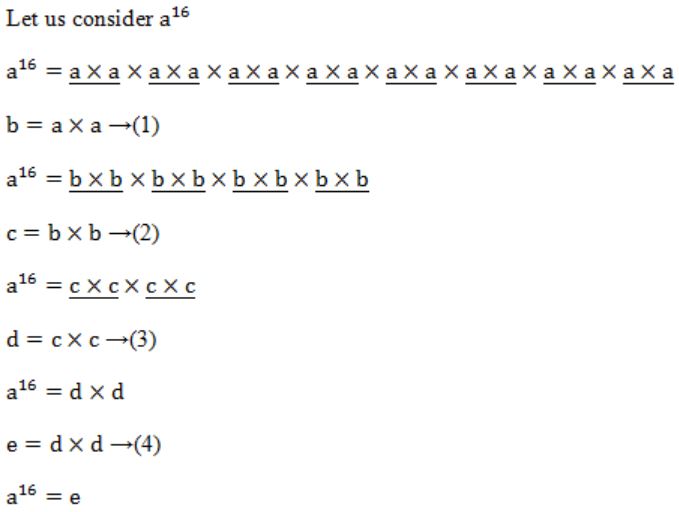
We require 4 multiplications to calculate a16 .....(I)
→ Like that 3 multiplications requires to calculate a8 .....(II)
I, II are satisfied with the option A.
Question 17 |
Which of the following is the most powerful parsing method?
LL (1) | |
Canonical LR | |
SLR | |
LALR |
LR > LALR > SLR
Question 18 |
Consider the join of a relation R with a relation S. If R has m tuples and S has n tuples then the maximum and minimum sizes of the join respectively are
m + n and 0 | |
mn and 0 | |
m + n and |m – n| | |
mn and m + n |
Suppose there is no common attribute in R and S due to which natural join will act as cross product. So then in cross product total no. of tuples will be mn.
For minimum:
Suppose there is common attribute in R and S, but none of the row of R matches with rows of S then minimum no. of tuples will be 0.
